.gif)
Order and disorder (physics)
Encyclopedia
In physics
, the terms order and disorder designate the presence or absence of some symmetry
or correlation
in a many-particle system.
In condensed matter physics
, systems typically are ordered at low temperatures; upon heating, they undergo one or several phase transition
s into less ordered states.
Examples for such an order-disorder transition are:
The degree of freedom that is ordered or disordered can be translational (crystal
line ordering), rotational (ferroelectric
ordering), or a spin state (magnetic
ordering).
The order can consist either in a full crystalline space group
symmetry, or in a correlation. Depending on how the correlations decay with distance, one speaks of long-range order or short-range order.
If a disordered state is not in thermodynamic equilibrium
, one speaks of quenched disorder. For instance, a glass
is obtained by quenching (supercooling) a liquid. By extension, other quenched states are called spin glass
, orientational glass
. In some contexts, the opposite of quenched disorder is annealed disorder.
of space. This is the defining property of a crystal
. Possible symmetries have been classified in 14 Bravais lattices and 230 space group
s.
Lattice periodicity implies long-range order: if only one unit cell is known, then by virtue of the translational symmetry it is possible to accurately predict all atomic positions at arbitrary distances. During much of the 20th century, the converse was also taken for granted - until the discovery of quasicrystal
s in 1982 showed that there are perfectly deterministic tilings that do not possess lattice periodicity.
Besides structural order, one may consider charge ordering
, spin
ordering, magnetic ordering, and compositional ordering. Magnetic ordering is observable in neutron diffraction
.
It is a thermodynamic entropy
concept often displayed by a second-order phase transition
. Generally speaking, high thermal energy is associated with disorder and low thermal energy with ordering, although there have been violations of this. Ordering peaks become apparent in diffraction experiments at low angles.
s in which remote portions of the same sample exhibit correlated
behavior.
This can be expressed as a correlation function
, namely the spin
-spin correlation function:
where s is the spin quantum number and x is the distance function within the particular system.
This function is equal to unity when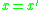 and decreases as the distance
and decreases as the distance 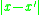 increases. Typically, it decays exponentially to zero at large distances, and the system is considered to be disordered. If, however, the correlation function decays to a constant value at large
increases. Typically, it decays exponentially to zero at large distances, and the system is considered to be disordered. If, however, the correlation function decays to a constant value at large 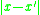 then the system is said to possess long-range order. If it decays to zero as a power of the distance then it is called quasi-long-range order
then the system is said to possess long-range order. If it decays to zero as a power of the distance then it is called quasi-long-range order
(for details see Chapter 11 in the textbook cited below. See also Berezinsky–Kosterlitz–Thouless transition
). Note that what constitutes a large value of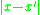 is relative.
is relative.
, a system is said to present quenched disorder when some parameters defining its behaviour are random variables which do not evolve with time, i.e.: they are quenched or frozen. Spin glass
es are a typical example. It is opposite to annealed disorder, where the random variables are allowed to evolve themselves.
In mathematical terms, quenched disorder is harder to analyze than its annealed counterpart, since the thermal and the noise averaging play very different roles. In fact, the problem is so hard that few techniques to approach each are known, most of them relying on approximations. The most used are the Replica Theory, a technique based on a mathematical analytical continuation known as the replica trick
and the Cavity method
which, although giving results in accord with experimentation in a large range of problems, is not generally proven to be a rigorous mathematical procedure.
More recently it has been shown by rigorous methods, however, that at least in the archetypal spin-glass model (the so-called Sherrington-Kirkpatrick model) the replica based solution is indeed exact; this area is still subject of research. The second most used technique in this field is generating functional analysis. This method is based on path integrals, and is in principle fully exact, although generally more difficult to apply than the replica procedure.
s, but whose evolution is related to that of the degrees of freedom
defining the system. It is defined in opposition to quenched disorder, where the random variables may not change its value.
Systems with annealed disorder are usually considered to be easier to deal with mathematically, since the average on the disorder and the thermal average may be treated on the same footing.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the terms order and disorder designate the presence or absence of some symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
or correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
in a many-particle system.
In condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, systems typically are ordered at low temperatures; upon heating, they undergo one or several phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s into less ordered states.
Examples for such an order-disorder transition are:
- the melting of ice: solid-liquid transition, loss of crystalline order;
- the demagnetization of iron by heating above the Curie temperature: ferromagnetic-paramagnetic transition, loss of magnetic order.
The degree of freedom that is ordered or disordered can be translational (crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
line ordering), rotational (ferroelectric
Ferroelectricity
Ferroelectricity is a property of certain materials which possess a spontaneous electric polarization that can be reversed by the application of an external electric field. The term is used in analogy to ferromagnetism, in which a material exhibits a permanent magnetic moment. Ferromagnetism was...
ordering), or a spin state (magnetic
Magnetism
Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well...
ordering).
The order can consist either in a full crystalline space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
symmetry, or in a correlation. Depending on how the correlations decay with distance, one speaks of long-range order or short-range order.
If a disordered state is not in thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, one speaks of quenched disorder. For instance, a glass
Glass
Glass is an amorphous solid material. Glasses are typically brittle and optically transparent.The most familiar type of glass, used for centuries in windows and drinking vessels, is soda-lime glass, composed of about 75% silica plus Na2O, CaO, and several minor additives...
is obtained by quenching (supercooling) a liquid. By extension, other quenched states are called spin glass
Spin glass
A spin glass is a magnet with frustrated interactions, augmented by stochastic disorder, where usually ferromagnetic and antiferromagnetic bonds are randomly distributed...
, orientational glass
Orientational glass
In solid-state physics, an orientational glass is a molecular solid in which crystalline long-range order coexists with quenched disorder in some rotational degree of freedom....
. In some contexts, the opposite of quenched disorder is annealed disorder.
Lattice periodicity and X-ray crystallinity
The strictest form of order in a solid is lattice periodicity: a certain pattern (the arrangement of atoms in a unit cell) is repeated again and again to form a translationally invariant tilingTiling
Tiling may refer to:* The physical act of laying tiles* The mathematics of tessellations* The compiler optimization of loop tiling* In computing, a tiling window manager, where windows do not overlap...
of space. This is the defining property of a crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
. Possible symmetries have been classified in 14 Bravais lattices and 230 space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s.
Lattice periodicity implies long-range order: if only one unit cell is known, then by virtue of the translational symmetry it is possible to accurately predict all atomic positions at arbitrary distances. During much of the 20th century, the converse was also taken for granted - until the discovery of quasicrystal
Quasicrystal
A quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...
s in 1982 showed that there are perfectly deterministic tilings that do not possess lattice periodicity.
Besides structural order, one may consider charge ordering
Charge ordering
Charge ordering is a phase transition occurring mostly in strongly correlated materials such as transition metal oxides or organic conductors. Due to the strong interaction, the charge is localized on different sites leading to a disproportionation and an ordered superlattice...
, spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
ordering, magnetic ordering, and compositional ordering. Magnetic ordering is observable in neutron diffraction
Neutron diffraction
Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material: A sample to be examined is placed in a beam of thermal or cold neutrons to obtain a diffraction pattern that provides information of...
.
It is a thermodynamic entropy
Entropy (order and disorder)
In thermodynamics, entropy is commonly associated with the amount of order, disorder, and/or chaos in a thermodynamic system. This stems from Rudolf Clausius' 1862 assertion that any thermodynamic processes always "admits to being reduced to the alteration in some way or another of the arrangement...
concept often displayed by a second-order phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
. Generally speaking, high thermal energy is associated with disorder and low thermal energy with ordering, although there have been violations of this. Ordering peaks become apparent in diffraction experiments at low angles.
Long-range order
Long-range order characterizes physical systemSystem
System is a set of interacting or interdependent components forming an integrated whole....
s in which remote portions of the same sample exhibit correlated
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
behavior.
This can be expressed as a correlation function
Correlation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
, namely the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
-spin correlation function:
where s is the spin quantum number and x is the distance function within the particular system.
This function is equal to unity when
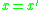 and decreases as the distance
and decreases as the distance 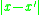 increases. Typically, it decays exponentially to zero at large distances, and the system is considered to be disordered. If, however, the correlation function decays to a constant value at large
increases. Typically, it decays exponentially to zero at large distances, and the system is considered to be disordered. If, however, the correlation function decays to a constant value at large 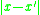 then the system is said to possess long-range order. If it decays to zero as a power of the distance then it is called quasi-long-range order
then the system is said to possess long-range order. If it decays to zero as a power of the distance then it is called quasi-long-range order(for details see Chapter 11 in the textbook cited below. See also Berezinsky–Kosterlitz–Thouless transition
Kosterlitz-Thouless transition
In statistical mechanics, a part of mathematical physics, the Kosterlitz–Thouless transition, or Berezinsky–Kosterlitz–Thouless transition, is a kind of phase transition that appears in the XY model in 2 spatial dimensions. The XY model is a 2-dimensional vector spin model that possesses U or...
). Note that what constitutes a large value of
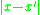 is relative.
is relative.Quenched disorder
In statistical physicsStatistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
, a system is said to present quenched disorder when some parameters defining its behaviour are random variables which do not evolve with time, i.e.: they are quenched or frozen. Spin glass
Spin glass
A spin glass is a magnet with frustrated interactions, augmented by stochastic disorder, where usually ferromagnetic and antiferromagnetic bonds are randomly distributed...
es are a typical example. It is opposite to annealed disorder, where the random variables are allowed to evolve themselves.
In mathematical terms, quenched disorder is harder to analyze than its annealed counterpart, since the thermal and the noise averaging play very different roles. In fact, the problem is so hard that few techniques to approach each are known, most of them relying on approximations. The most used are the Replica Theory, a technique based on a mathematical analytical continuation known as the replica trick
Replica trick
In statistical physics of spin glasses and other systems with quenched disorder, the replica trick is a mathematical technique based on the application of the formula- Mathematical Trick :...
and the Cavity method
Cavity method
The Cavity method is a mathematical method due to M. Mezard, Giorgio Parisi and Miguel Angel Virasoro in 1985 to solve some mean field type of models in statistical physics, specially adapted to disordered systems. It has been used to compute properties of ground states in many condensed matter and...
which, although giving results in accord with experimentation in a large range of problems, is not generally proven to be a rigorous mathematical procedure.
More recently it has been shown by rigorous methods, however, that at least in the archetypal spin-glass model (the so-called Sherrington-Kirkpatrick model) the replica based solution is indeed exact; this area is still subject of research. The second most used technique in this field is generating functional analysis. This method is based on path integrals, and is in principle fully exact, although generally more difficult to apply than the replica procedure.

Annealed disorder
A system is said to present annealed disorder when some parameters entering its definition are random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, but whose evolution is related to that of the degrees of freedom
Degrees of freedom
Degrees of freedom can mean:* Degrees of freedom , independent displacements and/or rotations that specify the orientation of the body or system...
defining the system. It is defined in opposition to quenched disorder, where the random variables may not change its value.
Systems with annealed disorder are usually considered to be easier to deal with mathematically, since the average on the disorder and the thermal average may be treated on the same footing.
See also
- In high energy physics, the formation of the chiral condensate in quantum chromodynamicsQuantum chromodynamicsIn theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
is an ordering transition; it is discussed in terms of superselectionSuperselectionIn Quantum mechanics, superselection extends the concept of selection rules.Superselection rules are postulated rules forbidding the preparation of quantum states that exhibit coherence between eigenstates of certain observables....
. - EntropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
- Topological orderTopological orderIn physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...
- ImpurityImpurityImpurities are substances inside a confined amount of liquid, gas, or solid, which differ from the chemical composition of the material or compound.Impurities are either naturally occurring or added during synthesis of a chemical or commercial product...
- superstructure (physics)
Further reading
- H Kleinert: Gauge Fields in Condensed Matter (ISBN 9971-5-0210-0, 2 volumes) Singapore: World Scientific (1989).


