
Omega and agemo subgroup
Encyclopedia
In mathematics
, or more specifically group theory
, the omega and agemo subgroups described the so-called "power structure" of a finite
p-group
. They were introduced in where they were used to describe a class of finite p-groups whose structure was sufficiently similar to that of finite abelian
p-groups, the so-called, regular p-group
s. The relationship between power and commutator structure forms a central theme in the modern study of p-groups, as exemplified in the work on uniformly powerful p-group
s.
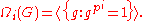
The agemo subgroups are the series of subgroups: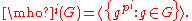
When i = 1 and p is odd, then i is normally omitted from the definition. When p is even, an omitted i may mean either i = 1 or i = 2 depending on local convention. In this article, we use the convention that an omitted i always indicates i = 1.
The quaternion group of order 8, H, satisfies Ω(H) = ℧(H) = Z(H) = [ H, H ] = Φ(H) = Soc(H) is the unique subgroup of order 2, normally realized as the subgroup containing only 1 and −1.
The Sylow p-subgroup, P, of the symmetric group
on p2 points is the wreath product
of two cyclic group
s of prime order. When p = 2, this is just the dihedral group of order 8. It too satisfies Ω(P) = P. Again ℧(P) = Z(P) = Soc(P) is cyclic of order p, but [ P, P ] = Φ(G) is elementary abelian of order pp−1.
The semidirect product
of a cyclic group of order 4 acting non-trivially on a cyclic group of order 4,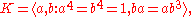
has ℧(K) elementary abelian of order 4, but the set of squares is simply { 1, aa, bb }. Here the element aabb of ℧(K) is not a square, showing that ℧ is not simply the set of squares.
|G| = pn and exponent exp(G) = pk have a number of useful properties.
General properties:
Behavior under quotients and subgroups:
If H ≤ G is a subgroup
of G and N ⊲ G is a normal subgroup
of G, then:
Relation to other important subgroups:
Relations in special classes of groups:
p-groups with abelian
p-groups in .
Groups in which Ω(G) ≤ Z(G) were studied by John G. Thompson
and have seen several more recent applications.
The dual notion, groups with [G,G] ≤ ℧(G) are called powerful p-groups and were introduced by Avinoam Mann. These groups were critical for the proof of the coclass conjectures which introduced an important way to understand the structure and classification of finite p-groups.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, or more specifically group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the omega and agemo subgroups described the so-called "power structure" of a finite
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
p-group
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
. They were introduced in where they were used to describe a class of finite p-groups whose structure was sufficiently similar to that of finite abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
p-groups, the so-called, regular p-group
Regular p-group
In mathematical finite group theory, the concept of regular p-group captures some of the more important properties of abelian p-groups, but is general enough to include most "small" p-groups...
s. The relationship between power and commutator structure forms a central theme in the modern study of p-groups, as exemplified in the work on uniformly powerful p-group
Powerful p-group
In mathematics, in the field of group theory, especially in the study of p-groups and pro-p-groups, the concept of powerful p-groups plays an important role. They were introduced in , where a number of applications are given, including results on Schur multipliers...
s.
Definition
The omega subgroups are the series of subgroups of a finite p-group, G, indexed by the natural numbers: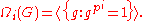
The agemo subgroups are the series of subgroups:
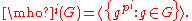
When i = 1 and p is odd, then i is normally omitted from the definition. When p is even, an omitted i may mean either i = 1 or i = 2 depending on local convention. In this article, we use the convention that an omitted i always indicates i = 1.
Examples
The dihedral group of order 8, G, satisfies: ℧(G) = Z(G) = [ G, G ] = Φ(G) = Soc(G) is the unique normal subgroup of order 2, typically realized as the subgroup containing the identity and a 180° rotation. However Ω(G) = G is the entire group, since G is generated by reflections. This shows that Ω(G) need not be the set of elements of order p.The quaternion group of order 8, H, satisfies Ω(H) = ℧(H) = Z(H) = [ H, H ] = Φ(H) = Soc(H) is the unique subgroup of order 2, normally realized as the subgroup containing only 1 and −1.
The Sylow p-subgroup, P, of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on p2 points is the wreath product
Wreath product
In mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
of two cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s of prime order. When p = 2, this is just the dihedral group of order 8. It too satisfies Ω(P) = P. Again ℧(P) = Z(P) = Soc(P) is cyclic of order p, but [ P, P ] = Φ(G) is elementary abelian of order pp−1.
The semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of a cyclic group of order 4 acting non-trivially on a cyclic group of order 4,
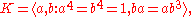
has ℧(K) elementary abelian of order 4, but the set of squares is simply { 1, aa, bb }. Here the element aabb of ℧(K) is not a square, showing that ℧ is not simply the set of squares.
Properties
In this section, let G be a finite p-group of orderOrder (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
|G| = pn and exponent exp(G) = pk have a number of useful properties.
General properties:
- Both Ωi(G) and ℧i(G) are characteristic subgroupCharacteristic subgroupIn mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is invariant under all automorphisms of the parent group. Because conjugation is an automorphism, every characteristic subgroup is normal, though not every normal...
s of G for all natural numbers, i. - The omega and agemo subgroups form two normal seriesNormal seriesIn mathematics, a subgroup series is a chain of subgroups:1 = A_0 \leq A_1 \leq \cdots \leq A_n = G.Subgroup series can simplify the study of a group to the study of simpler subgroups and their relations, and several subgroup series can be invariantly defined and are important invariants of groups...
:
-
- G = ℧0(G) ≥ ℧1(G) ≥ ℧2(G) ≥ ... ≥ ℧k−2(G) ≥ ℧k−1(G) > ℧k(G) = 1
- G = Ωk(G) ≥ Ωk−1(G) ≥ Ωk−2(G) ≥ ... ≥ Ω2(G) ≥ Ω1(G) > Ω0(G) = 1
- and the series are loosely intertwined: For all i between 1 and k:
- ℧i(G) ≤ Ωk−i(G), but
- ℧i−1(G) is not contained in Ωk−i(G).
Behavior under quotients and subgroups:
If H ≤ G is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G and N ⊲ G is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G, then:
- ℧i(H) ≤ H ∩ ℧i(G)
- Ωi(H) = H ∩ Ωi(G)
- ℧i(N) ⊲ G
- Ωi(N) ⊲ G
- ℧i(G/N) = ℧i(G)N/N
- Ωi(G/N) ≥ Ωi(G)N/N
Relation to other important subgroups:
- Soc(G) = Ω(Z(G)), the subgroup consisting of central elements of order p is the socleSocle (mathematics)-Socle of a group:In the context of group theory, the socle of a group G, denoted Soc, is the subgroup generated by the minimal non-trivial normal subgroups of G. The socle is a direct product of minimal normal subgroups...
, Soc(G), of G - Φ(G) = ℧(G)[G,G], the subgroup generated by all pth powers and commutators is the Frattini subgroupFrattini subgroupIn mathematics, the Frattini subgroup Φ of a group G is the intersection of all maximal subgroups of G. For the case that G is the trivial group e, which has no maximal subgroups, it is defined by Φ = e...
, Φ(G), of G.
Relations in special classes of groups:
- In an abelian p-group, or more generally in a regular p-group:
-
- |℧i(G)|⋅|Ωi(G)| = |G|
- [℧i(G):℧i+1(G)] = [Ωi(G):Ωi+1(G)],
- where |H| is the orderOrder (group theory)In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of H and [H:K] = |H|/|K| denotes the index of the subgroups K ≤ H.
Applications
The first application of the omega and agemo subgroups was to draw out the analogy of regularRegular p-group
In mathematical finite group theory, the concept of regular p-group captures some of the more important properties of abelian p-groups, but is general enough to include most "small" p-groups...
p-groups with abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
p-groups in .
Groups in which Ω(G) ≤ Z(G) were studied by John G. Thompson
John G. Thompson
John Griggs Thompson is a mathematician at the University of Florida noted for his work in the field of finite groups. He was awarded the Fields Medal in 1970, the Wolf Prize in 1992 and the 2008 Abel Prize....
and have seen several more recent applications.
The dual notion, groups with [G,G] ≤ ℧(G) are called powerful p-groups and were introduced by Avinoam Mann. These groups were critical for the proof of the coclass conjectures which introduced an important way to understand the structure and classification of finite p-groups.

