Null graph
Encyclopedia
In the mathematical
field of graph theory
, the null graph may refer either to the order zero graph
, or alternatively, to any edgeless graph (the latter is sometimes called an empty graph).
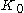is the unique graph of order zero (having zero vertices
). As a consequence, it also has zero edges. In some contexts,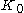
is excluded from being considered a graph (either by definition, or more simply as a matter of convenience).
The order zero graph is the initial object
in the category
of graphs, according to some definitions of a category of graphs. Its inclusion within the definition of graph theory is more useful in some contexts than others. On the positive side,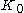
follows naturally from the usual set-theoretic
definitions of a graph (it is the ordered pair
of empty sets
), and in recursively defined
data structures
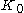is useful for defining the base case for recursion (by treating the null tree
as the child of missing edges in any non-null binary tree
, every non-null binary tree has exactly two children). On the negative side, most well-defined formulas for graph properties must include exceptions for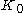
if it is included as a graph ("counting all strongly-connected components
of a graph" would become "counting all non-null strongly-connected components of a graph"). Due to the undesirable aspects, it is usually assumed in literature that the term "graph" implies "graph with at least one vertex" unless context suggests otherwise.
When acknowledged,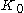
fulfills (vacuously
) most of the same basic graph properties as
(the graph with one vertex and no edges): it has a size of zero, it is equal to its complement graph
(
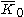), it is a connected component
(namely,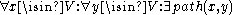
), an acyclic graph, a tree
, an arboricity
, a forest, it may be an undirected graph or a directed graph
(or even both), and it is both a complete graph
and an empty graph (just to name a few). However, definitions for each of these graph properties will vary depending on whether context allows for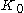
. For example, the term "connected component" almost always excludes 
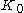, whereas trees as data structures
often include the "null tree" case.
n, the edgeless graph (or empty graph)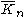
is the graph with n vertices and zero edges. An edgeless graph is occasionally referred to as a null graph in contexts where the order zero graph is not permitted.
The n-vertex edgeless graph is the complement graph
for the complete graph
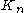, and therefore it is commonly denoted as 
.
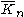Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the null graph may refer either to the order zero graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, or alternatively, to any edgeless graph (the latter is sometimes called an empty graph).
Order zero graph
The order zero graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
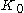is the unique graph of order zero (having zero verticesVertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
). As a consequence, it also has zero edges. In some contexts,
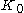is excluded from being considered a graph (either by definition, or more simply as a matter of convenience).The order zero graph is the initial object
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of graphs, according to some definitions of a category of graphs. Its inclusion within the definition of graph theory is more useful in some contexts than others. On the positive side,
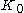follows naturally from the usual set-theoreticSet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
definitions of a graph (it is the ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
of empty sets
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
), and in recursively defined
Recursive definition
In mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
data structures
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
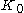is useful for defining the base case for recursion (by treating the null treeTree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
as the child of missing edges in any non-null binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
, every non-null binary tree has exactly two children). On the negative side, most well-defined formulas for graph properties must include exceptions for
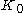if it is included as a graph ("counting all strongly-connected componentsConnected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
of a graph" would become "counting all non-null strongly-connected components of a graph"). Due to the undesirable aspects, it is usually assumed in literature that the term "graph" implies "graph with at least one vertex" unless context suggests otherwise.
When acknowledged,
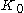fulfills (vacuouslyVacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
) most of the same basic graph properties as
(the graph with one vertex and no edges): it has a size of zero, it is equal to its complement graphComplement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
(
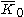), it is a connected componentConnected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
(namely,
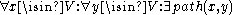), an acyclic graph, a treeTree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, an arboricity
Arboricity
The arboricity of an undirected graph is the minimum number of forests into which its edges can be partitioned. Equivalently it is the minimum number of spanning forests needed to cover all the edges of the graph.-Example:...
, a forest, it may be an undirected graph or a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
(or even both), and it is both a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
and an empty graph (just to name a few). However, definitions for each of these graph properties will vary depending on whether context allows for
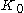. For example, the term "connected component" almost always excludes 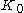, whereas trees as data structuresTree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
often include the "null tree" case.
Edgeless graph
For each natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n, the edgeless graph (or empty graph)
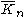is the graph with n vertices and zero edges. An edgeless graph is occasionally referred to as a null graph in contexts where the order zero graph is not permitted.The n-vertex edgeless graph is the complement graph
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
for the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
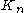, and therefore it is commonly denoted as .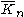