
Tree (data structure)
Encyclopedia
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a tree is a widely-used data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
that emulates a hierarchical tree structure
Tree structure
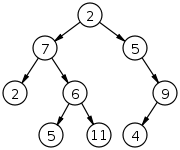
A tree structure is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, even though the chart is generally upside down compared to an actual tree, with the "root" at the top and the...
with a set of linked nodes
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
.
Mathematically, it is an ordered directed tree, more specifically an arborescence
Arborescence (graph theory)
In graph theory, an arborescence is a directed graph in which, for a vertex u called the root and any other vertex v, there is exactly one directed path from u to v....
: an acyclic connected graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
where each node has zero or more children nodes and at most one parent node. Furthermore, the children of each node have a specific order.
Terminology
A nodeNode (computer science)
A node is a record consisting of one or more fields that are links to other nodes, and a data field. The link and data fields are often implemented by pointers or references although it is also quite common for the data to be embedded directly in the node. Nodes are used to build linked, often...
is a structure which may contain a value, a condition, or represent a separate data structure (which could be a tree of its own). Each node in a tree has zero or more child nodes, which are below it in the tree (by convention, trees are drawn growing downwards). A node that has a child is called the child's parent node (or ancestor node, or superior
Superior (hierarchy)
In a hierarchy or tree structure of any kind, a superior is an individual or position at a higher level in the hierarchy than another , and thus closer to the apex. It is often used in business terminology to refer to people who are supervisors and in the military to people who are higher in the...
). A node has at most one parent.
An internal node or inner node is any node of a tree that has child nodes. Similarly, an external node (also known as an outer node, leaf node, or terminal node) is any node that does not have child nodes.
The topmost node in a tree is called the root node. Being the topmost node, the root node will not have a parent. It is the node at which operations on the tree commonly begin (although some algorithms begin with the leaf nodes and work up ending at the root). All other nodes can be reached from it by following edges or links. (In the formal definition, each such path is also unique). In diagrams, it is typically drawn at the top. In some trees, such as heaps
Heap (data structure)
In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: if B is a child node of A, then key ≥ key. This implies that an element with the greatest key is always in the root node, and so such a heap is sometimes called a max-heap...
, the root node has special properties. Every node in a tree can be seen as the root node of the subtree rooted at that node. A free tree is a tree that is not rooted.
The height of a node is the length of the longest downward path to a leaf from that node. The height of the root is the height of the tree. The depth of a node is the length of the path to its root (i.e., its root path). This is commonly needed in the manipulation of the various self balancing trees, AVL Trees in particular. Conventionally, the value −1 corresponds to a subtree with no nodes, whereas zero corresponds to a subtree with one node.
A subtree of a tree T is a tree consisting of a node in T and all of its descendants in T. (This is different from the formal definition of subtree used in graph theory.) The subtree corresponding to the root node is the entire tree; the subtree corresponding to any other node is called a proper subtree (in analogy to the term proper subset).
Representations
There are many different ways to represent trees; common representations represent the nodes as dynamically allocated records with pointers to their children, their parents, or both, or as items in an array, with relationships between them determined by their positions in the array (e.g., binary heapBinary heap
A binary heap is a heap data structure created using a binary tree. It can be seen as a binary tree with two additional constraints:*The shape property: the tree is a complete binary tree; that is, all levels of the tree, except possibly the last one are fully filled, and, if the last level of...
).
Trees and graphs
The tree data structure can be generalized to represent directed graphDirected graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
s by removing the constraints that a node may have at most one parent, and that no cycles are allowed. Edges are still abstractly considered as pairs of nodes, however, the terms parent and child are usually replaced by different terminology (for example, source and target). Different implementation strategies exist, for example adjacency list
Adjacency list
In graph theory, an adjacency list is the representation of all edges or arcs in a graph as a list.If the graph is undirected, every entry is a set of two nodes containing the two ends of the corresponding edge; if it is directed, every entry is a tuple of two nodes, one denoting the source node...
s.
Relationship with trees in graph theory
In graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
is a connected acyclic graph
Graph (data structure)
In computer science, a graph is an abstract data structure that is meant to implement the graph and hypergraph concepts from mathematics.A graph data structure consists of a finite set of ordered pairs, called edges or arcs, of certain entities called nodes or vertices...
; unless stated otherwise, trees and graphs are undirected. There is no one-to-one correspondence between such trees and trees as data structure. We can take an arbitrary undirected tree, arbitrarily pick one of its vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
as the root, make all its edges directed by making them point away from the root node - producing an arborescence
Arborescence (graph theory)
In graph theory, an arborescence is a directed graph in which, for a vertex u called the root and any other vertex v, there is exactly one directed path from u to v....
- and assign an order to all the nodes. The result corresponds to a tree data structure. Picking a different root or different ordering produces a different one.
Traversal methods
Stepping through the items of a tree, by means of the connections between parents and children, is called walking the tree, and the action is a walk of the tree. Often, an operation might be performed when a pointer arrives at a particular node. A walk in which each parent node is traversed before its children is called a pre-order walk; a walk in which the children are traversed before their respective parents are traversed is called a post-order walk; a walk in which a node's left subtree, then the node itself, and then finally its right subtree are traversed is called an in-order traversal. (This last scenario, referring to exactly two subtrees, a left subtree and a right subtree, assumes specifically a binary treeBinary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
.)
Here inorder is like infix expression,postorder is like postfix expression and preorder is like prefix expression.
Common operations
- Enumerating all the items
- Enumerating a section of a tree
- Searching for an item
- Adding a new item at a certain position on the tree
- Deleting an item
- Removing a whole section of a tree (called pruningPruning (algorithm)Pruning is a technique in machine learning that reduces the size of decision trees by removing sections of the tree that provide little power to classify instances...
) - Adding a whole section to a tree (called graftingGrafting (algorithm)In computer science, grafting is a method used to manipulate trees. One such tree is an ordered tree, which is where the subtrees for any node are ordered. Let root, ..., root be the children of root and root be the ith child...
) - Finding the root for any node
Common uses
- Manipulate hierarchical data
- Make information easy to searchSearch algorithmIn computer science, a search algorithm is an algorithm for finding an item with specified properties among a collection of items. The items may be stored individually as records in a database; or may be elements of a search space defined by a mathematical formula or procedure, such as the roots...
(see tree traversalTree traversalIn computer science, tree-traversal refers to the process of visiting each node in a tree data structure, exactly once, in a systematic way. Such traversals are classified by the order in which the nodes are visited...
and binary search treeBinary search treeIn computer science, a binary search tree , which may sometimes also be called an ordered or sorted binary tree, is a node-based binary tree data structurewhich has the following properties:...
) - Manipulate sorted listsSorting algorithmIn computer science, a sorting algorithm is an algorithm that puts elements of a list in a certain order. The most-used orders are numerical order and lexicographical order...
of data - As a workflow for compositingDigital compositingDigital compositing is the process of digitally assembling multiple images to make a final image, typically for print, motion pictures or screen display...
digital images for visual effectsVisual effectsVisual effects are the various processes by which imagery is created and/or manipulated outside the context of a live action shoot. Visual effects involve the integration of live-action footage and generated imagery to create environments which look realistic, but would be dangerous, costly, or... - Router algorithms
See also
- Tree structureTree structureA tree structure is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, even though the chart is generally upside down compared to an actual tree, with the "root" at the top and the...
- Tree (graph theory)Tree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
- Tree (set theory)Tree (set theory)In set theory, a tree is a partially ordered set In set theory, a tree is a partially ordered set (poset) In set theory, a tree is a partially ordered set (poset) (T, In set theory, a tree is a partially ordered set (poset) (T, ...
- Hierarchy (mathematics)Hierarchy (mathematics)In mathematics, a hierarchy is a preorder, i.e. an ordered set. The term is used to stress a natural hierarchical relation among the elements. In particular, it is the preferred terminology for posets whose elements are classes of objects of increasing complexity. In that case, the preorder...
- Dialog tree
Other trees
- DSW algorithmDSW algorithmThe DSW algorithm, or in full Day/Stout/Warren algorithm, is a method for efficiently balancing binary search trees — that is, decreasing their height to O nodes, where n is the total number of nodes...
- EnfiladeEnfilade (Xanadu)Enfilades are a class of tree data structures used in Project Xanadu designs of the 1970s and 1980s. Enfilades allow quick editing, versioning, retrieval and inter-comparison operations in a large, cross-linked hypertext database...
- Left child-right sibling binary treeLeft child-right sibling binary treeIn computer science, a left child-right sibling binary tree is a binary tree representation of a k-ary tree. The process of converting from a k-ary tree to an LC-RS binary tree is not reversible in general without additional information....
External links
- Description from the Dictionary of Algorithms and Data StructuresDictionary of Algorithms and Data StructuresThe Dictionary of Algorithms and Data Structures is a dictionary style reference for many of the algorithms, algorithmic techniques, archetypal problems and data structures found in the field of computer science. The dictionary is maintained by Paul E...
- STL-like C++ tree class
- Description of tree data structures from ideainfo.8m.com
- flash actionscript 3 opensource implementation of tree and binary tree — opensource library
- WormWeb.org: Interactive Visualization of the C. elegans Cell Tree - Visualize the entire cell lineage tree of the nematode C. elegans (javascript)

