Nuclear space
Encyclopedia
In mathematics
, a nuclear space is a topological vector space
with many of the good properties of finite-dimensional vector spaces. The topology on them can be defined by a family of seminorms whose unit balls decrease rapidly in size. Vector spaces whose elements are "smooth" in some sense tend to be nuclear spaces; a typical example of a nuclear space is the set of smooth functions on a compact manifold. Although important, nuclear spaces are not widely used, possibly because the definition is notoriously difficult to understand.
Much of the theory of nuclear spaces was developed by Alexander Grothendieck
and published in .
. (This means that the space is complete and the topology is given by a countable family of seminorms.)
We start by recalling some background. A locally convex topological vector space
V has a topology that is defined by some family of seminorms. For any seminorm, the unit ball is a closed convex symmetric neighborhood of 0, and conversely any closed convex symmetric neighborhood of 0 is the unit ball of some seminorm. (For complex vector spaces, the condition "symmetric" should be replaced by "balanced
".)
If p is a seminorm on V, we write Vp for the Banach space
given by completing V using the seminorm p. There is a natural map from V to Vp (not necessarily injective).
Definition 1: A nuclear space is a locally convex topological vector space such that for any seminorm p we can find a larger seminorm q so that the natural map from Vq to Vp is nuclear
.
Informally, this means that whenever we are given the unit ball of some seminorm, we can find a "much smaller" unit ball of another seminorm inside it, or that any neighborhood of 0 contains a "much smaller" neighborhood. It is not necessary to check this condition for all seminorms p; it is sufficient to check it for a set of seminorms that generate the topology, in other words, a set of seminorms that are a subbase
for the topology.
Instead of using arbitrary Banach spaces and nuclear operators, we can give a definition in terms of Hilbert space
s and trace class
operators, which are easier to understand.
(On Hilbert spaces nuclear operators are often called trace class operators.)
We will say that a seminorm p is a Hilbert seminorm if Vp is a Hilbert space, or equivalently if p comes from a sesquilinear positive semidefinite form on V.
Definition 2: A nuclear space is a topological vector space with a topology defined by a family of Hilbert seminorms, such that for any Hilbert seminorm p we can find a larger Hilbert seminorm q so that the natural map from Vq to Vp is trace class
.
Some authors prefer to use Hilbert-Schmidt operators rather than trace class operators. This makes little difference, because any trace class operator is Hilbert-Schmidt, and the product of two Hilbert-Schmidt operators is of trace class.
Definition 3: A nuclear space is a topological vector space with a topology defined by a family of Hilbert seminorms, such that for any Hilbert seminorm p we can find a larger Hilbert seminorm q so that the natural map from Vq to Vp is Hilbert-Schmidt.
If we are willing to use the concept of a nuclear operator from an arbitrary locally convex topological vector space to a Banach space, we can give shorter definitions as follows:
Definition 4: A nuclear space is a locally convex topological vector space such that for any seminorm p the natural map from V to Vp is nuclear
.
Definition 5: A nuclear space is a locally convex topological vector space such that any continuous linear map to a Banach space is nuclear.
Grothendieck used a definition similar to the following one:
Definition 6: A nuclear space is a locally convex topological vector space A such that for any locally convex topological vector space B the natural map from the projective to the injective tensor product of A and B is an isomorphism.
In fact it is sufficient to check this just for Banach spaces B, or even just for the single Banach space l1 of absolutely convergent series.
There are no Banach spaces that are nuclear, except for the finite-dimensional ones. In practice a sort of converse to this is often true: if a "naturally occurring" topological vector space is not a Banach space, then there is a good chance that it is nuclear.
If the completion in this norm is Cs, then there is a natural map from Cs to Ct whenever s≥t, and this is nuclear whenever s>t+1, essentially because the series Σnt−s is then absolutely convergent. In particular for each norm ||·||t we can find another norm, say ||·||t+2,
such that the map from Ct+2 to Ct is nuclear. So the space is nuclear.
and 
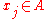, j,k=1,...,n,
.
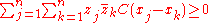Given a characteristic functional on a nuclear space A, the Bochner–Minlos theorem (after Salomon Bochner
and Robert Adol'fovich Minlos
) guarantees the existence and uniqueness of the corresponding probability measure
on the dual space 
, given by
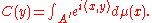
This extends the inverse Fourier transform to nuclear spaces.
In particular, if A is the nuclear space
,
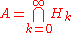where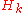
are Hilbert spaces, the Bochner–Minlos theorem guarantees the existence of a probability measure with the characteristic function 
, that is, the existence of the Gaussian measure on the dual space
. Such measure is called white noise
measure. When A is the Schwartz space, the corresponding random element
is a random distribution
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a nuclear space is a topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
with many of the good properties of finite-dimensional vector spaces. The topology on them can be defined by a family of seminorms whose unit balls decrease rapidly in size. Vector spaces whose elements are "smooth" in some sense tend to be nuclear spaces; a typical example of a nuclear space is the set of smooth functions on a compact manifold. Although important, nuclear spaces are not widely used, possibly because the definition is notoriously difficult to understand.
Much of the theory of nuclear spaces was developed by Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
and published in .
Definition
This section lists some of the more common definitions of a nuclear space. The definitions below are all equivalent. Note that some authors use a more restrictive definition of a nuclear space, by adding the condition that the space should be FréchetFréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
. (This means that the space is complete and the topology is given by a countable family of seminorms.)
We start by recalling some background. A locally convex topological vector space
Locally convex topological vector space
In functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
V has a topology that is defined by some family of seminorms. For any seminorm, the unit ball is a closed convex symmetric neighborhood of 0, and conversely any closed convex symmetric neighborhood of 0 is the unit ball of some seminorm. (For complex vector spaces, the condition "symmetric" should be replaced by "balanced
Balanced set
In linear algebra and related areas of mathematics a balanced set, circled set or disk in a vector space is a set S so that for all scalars α with |α| ≤ 1\alpha S \subseteq S...
".)
If p is a seminorm on V, we write Vp for the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
given by completing V using the seminorm p. There is a natural map from V to Vp (not necessarily injective).
Definition 1: A nuclear space is a locally convex topological vector space such that for any seminorm p we can find a larger seminorm q so that the natural map from Vq to Vp is nuclear
Nuclear operator
In mathematics, a nuclear operator is roughly a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis .Nuclear operators are essentially the same as trace class operators, though most authors reserve the term "trace...
.
Informally, this means that whenever we are given the unit ball of some seminorm, we can find a "much smaller" unit ball of another seminorm inside it, or that any neighborhood of 0 contains a "much smaller" neighborhood. It is not necessary to check this condition for all seminorms p; it is sufficient to check it for a set of seminorms that generate the topology, in other words, a set of seminorms that are a subbase
Subbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
for the topology.
Instead of using arbitrary Banach spaces and nuclear operators, we can give a definition in terms of Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s and trace class
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
operators, which are easier to understand.
(On Hilbert spaces nuclear operators are often called trace class operators.)
We will say that a seminorm p is a Hilbert seminorm if Vp is a Hilbert space, or equivalently if p comes from a sesquilinear positive semidefinite form on V.
Definition 2: A nuclear space is a topological vector space with a topology defined by a family of Hilbert seminorms, such that for any Hilbert seminorm p we can find a larger Hilbert seminorm q so that the natural map from Vq to Vp is trace class
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
.
Some authors prefer to use Hilbert-Schmidt operators rather than trace class operators. This makes little difference, because any trace class operator is Hilbert-Schmidt, and the product of two Hilbert-Schmidt operators is of trace class.
Definition 3: A nuclear space is a topological vector space with a topology defined by a family of Hilbert seminorms, such that for any Hilbert seminorm p we can find a larger Hilbert seminorm q so that the natural map from Vq to Vp is Hilbert-Schmidt.
If we are willing to use the concept of a nuclear operator from an arbitrary locally convex topological vector space to a Banach space, we can give shorter definitions as follows:
Definition 4: A nuclear space is a locally convex topological vector space such that for any seminorm p the natural map from V to Vp is nuclear
Nuclear operator
In mathematics, a nuclear operator is roughly a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis .Nuclear operators are essentially the same as trace class operators, though most authors reserve the term "trace...
.
Definition 5: A nuclear space is a locally convex topological vector space such that any continuous linear map to a Banach space is nuclear.
Grothendieck used a definition similar to the following one:
Definition 6: A nuclear space is a locally convex topological vector space A such that for any locally convex topological vector space B the natural map from the projective to the injective tensor product of A and B is an isomorphism.
In fact it is sufficient to check this just for Banach spaces B, or even just for the single Banach space l1 of absolutely convergent series.
Examples
- Any finite-dimensional vector space is nuclear, because any operator on a finite-dimensional vector space is nuclear.
There are no Banach spaces that are nuclear, except for the finite-dimensional ones. In practice a sort of converse to this is often true: if a "naturally occurring" topological vector space is not a Banach space, then there is a good chance that it is nuclear.
- The simplest infinite example of a nuclear space is the space of all rapidly decreasing sequences c=(c1, c2,...). ("Rapidly decreasing" means that cnp(n) is bounded for any polynomial p.) For each real number s, we can define a norm ||·||s by
- ||c||s = sup |cn|ns
If the completion in this norm is Cs, then there is a natural map from Cs to Ct whenever s≥t, and this is nuclear whenever s>t+1, essentially because the series Σnt−s is then absolutely convergent. In particular for each norm ||·||t we can find another norm, say ||·||t+2,
such that the map from Ct+2 to Ct is nuclear. So the space is nuclear.
- The space of smooth functions on any compact manifold is nuclear.
- The Schwartz space of smooth functions on
for which the derivatives of all orders are rapidly decreasing is a nuclear space.
- The space of entire holomorphic functions on the complex plane is nuclear.
- The inductive limit of a sequence of nuclear spaces is nuclear.
- The strong dual of a nuclear Frechet space is nuclear.
- The product of a family of nuclear spaces is nuclear.
- The completion of a nuclear space is nuclear (and in fact a space is nuclear if and only if its completion is nuclear).
- The tensor productTopological tensor productIn mathematics, there are usually many different ways to construct a topological tensor product of two topological vector spaces. For Hilbert spaces or nuclear spaces there is a simple well-behaved theory of tensor products , but for general Banach spaces or locally convex topological vector space...
of two nuclear spaces is nuclear.
Properties
Nuclear spaces are in many ways similar to finite-dimensional spaces and have many of their good properties.- A closed bounded subset of a nuclear Frechet space is compact. (A bounded subset B of a topological vector space is one such that for any neighborhood U of 0 we can find a positive real scalar λ such that B is contained in λU.) This statement may be paraphrased as a Heine-Borel theorem for nuclear Frechet spaces, analogous to the finite-dimensional situation.
- Any subspace and any quotient space by a closed subspace of a nuclear space is nuclear.
- If A is nuclear and B is any locally convex topological vector space, then the natural map from the projective tensor product of A and B to the injective tensor product is an isomorphism. Roughly speaking this means that there is only one sensible way to define the tensor product. This property characterizes nuclear spaces A.
- In the theory of measures on topological vector spaces, a basic theorem states that any continuous cylinder set measureCylinder set measureIn mathematics, cylinder set measure is a kind of prototype for a measure on an infinite-dimensional vector space...
on the dual of a nuclear Frechet space automatically extends to a Radon measureRadon measureIn mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
. This is useful because it is often easy to construct cylinder set measures on topological vector spaces, but these are not good enough for most applications unless they are Radon measures (for example, they are not even countably additive in general).
Bochner–Minlos theorem
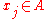A continuous functional C on a nuclear space A is called a characteristic functional if C(0)=1, and for any complex and , j,k=1,...,n,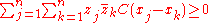.Given a characteristic functional on a nuclear space A, the Bochner–Minlos theorem (after Salomon Bochner
Salomon Bochner
Salomon Bochner was an American mathematician of Austrian-Hungarian origin, known for wide-ranging work in mathematical analysis, probability theory and differential geometry.- Life :...
and Robert Adol'fovich Minlos
Robert Adol'fovich Minlos
Robert Adol'fovich Minlos is a Soviet and Russian mathematician who has made important contributions to probability theory and mathematical physics...
) guarantees the existence and uniqueness of the corresponding probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on the dual space , given by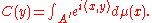This extends the inverse Fourier transform to nuclear spaces.
In particular, if A is the nuclear space
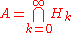,where
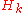are Hilbert spaces, the Bochner–Minlos theorem guarantees the existence of a probability measure with the characteristic function , that is, the existence of the Gaussian measure on the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
. Such measure is called white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
measure. When A is the Schwartz space, the corresponding random element
Random element
In probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line...
is a random distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
.