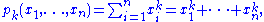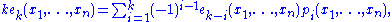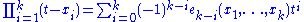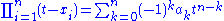Newton's identities
Encyclopedia
In mathematics
, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomial
s, namely between power sums
and elementary symmetric polynomial
s. Evaluated at the roots of a monic polynomial
P in one variable, they allow expressing the sums of the k-th powers of all roots of P (counted with their multiplicity) in terms of the coefficients of P, without actually finding those roots. These identities were found by Isaac Newton
around 1666, apparently in ignorance of earlier work (1629) by Albert Girard
. They have applications in many areas of mathematics, including Galois theory
, invariant theory
, group theory
, combinatorics
, as well as further applications outside mathematics, including general relativity
.
and for k ≥ 0 denote by ek(x1,…,xn) the elementary symmetric polynomial
that is the sum of all distinct products of k distinct variables, so in particular
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s, namely between power sums
Power sum symmetric polynomial
In mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric...
and elementary symmetric polynomial
Elementary symmetric polynomial
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
s. Evaluated at the roots of a monic polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
P in one variable, they allow expressing the sums of the k-th powers of all roots of P (counted with their multiplicity) in terms of the coefficients of P, without actually finding those roots. These identities were found by Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
around 1666, apparently in ignorance of earlier work (1629) by Albert Girard
Albert Girard
Albert Girard was a French-born mathematician. He studied at the University of Leiden. He "had early thoughts on the fundamental theorem of algebra" and gave the inductive definition for the Fibonacci numbers....
. They have applications in many areas of mathematics, including Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
, group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, as well as further applications outside mathematics, including general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
Formulation in terms of symmetric polynomials
Let x1,…, xn be variables, denote for k ≥ 1 by pk(x1,…,xn) the k-th power sum:and for k ≥ 0 denote by ek(x1,…,xn) the elementary symmetric polynomial
Elementary symmetric polynomial
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
that is the sum of all distinct products of k distinct variables, so in particular
-
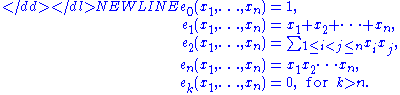
Then the Newton's identities can be stated as
valid for all k ≥ 1. Concretely, one gets for the first few values of k:
-
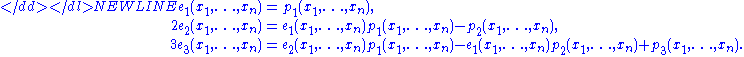
The form and validity of these equations do not depend on the number n of variables (although the point where the left-hand side becomes 0 does, namely after the n-th identity), which makes it possible to state them as identities in the ring of symmetric functions. In that ring one has
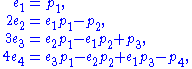
and so on; here the left-hand sides never become zero.
These equations allow to recursively express the ei in terms of the pk; to be able to do the inverse, one may rewrite them as
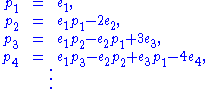
Application to the roots of a polynomial
Now view the xi as parameters rather than as variables, and consider the monic polynomial in t with roots x1,…,xn:

where the coefficients are given by the elementary symmetric polynomials in the roots: ak = ek(x1,…,xn).
are given by the elementary symmetric polynomials in the roots: ak = ek(x1,…,xn).
Now consider the power sums of the roots

Then according to Newton's identities these can be expressed recursively in terms of the coefficients of the polynomial using
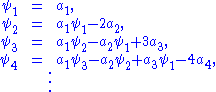
Application to the characteristic polynomial of a matrix
When the polynomial above is the characteristic polynomialCharacteristic polynomialIn linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of a matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A, the roots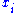 are the eigenvalues of the matrix, counted with their algebraic multiplicity. For any positive integer k, the matrix Ak has as eigenvalues the powers xik, and each eigenvalue
are the eigenvalues of the matrix, counted with their algebraic multiplicity. For any positive integer k, the matrix Ak has as eigenvalues the powers xik, and each eigenvalue 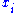 of A contributes its multiplicity to that of the eigenvalue xik of Ak. Then the coefficients of the characteristic polynomial of Ak are given by the elementary symmetric polynomials in those powers xik. In particular, the sum of the xik, which is the k-th power sum ψk of the roots of the characteristic polynomial of A, is given by its traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of A contributes its multiplicity to that of the eigenvalue xik of Ak. Then the coefficients of the characteristic polynomial of Ak are given by the elementary symmetric polynomials in those powers xik. In particular, the sum of the xik, which is the k-th power sum ψk of the roots of the characteristic polynomial of A, is given by its traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
:

The Newton identities now relate the traces of the powers Ak to the coefficients of the characteristic polynomial of A. Using them in reverse to express the elementary symmetric polynomials in terms of the power sums, they can be used to find the characteristic polynomial by computing only the powers Ak and their traces.
Relation with Galois theory
For a given n, the elementary symmetric polynomials ek(x1,…,xn) for k = 1,…, n form an algebraic basis for the space of symmetric polynomials in x1,…. xn: every polynomial expression in the xi that is invariant under all permutations of those variables is given by a polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
expression in those elementary symmetric polynomials, and this expression is unique up to equivalence of polynomial expressions. This is a general fact known as the fundamental theorem of symmetric polynomials, and Newton's identities provide explicit formulae in the case of power sum symmetric polynomials. Applied to the monic polynomial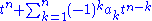 with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theoryGalois theoryIn mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theoryGalois theoryIn mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
Related identities
There is a number of (families of) identities that, while they should be distinguished from Newton's identities, are very closely related to them.
A variant using complete homogeneous symmetric polynomials
Denoting by hk the complete homogeneous symmetric polynomialComplete homogeneous symmetric polynomialIn mathematics, specifically in algebraic combinatorics and commutative algebra, the complete homogeneous symmetric polynomials are a specific kind of symmetric polynomials...
that is the sum of all monomialMonomialIn mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s of degree k, the power sum polynomials also satisfy identities similar to Newton's identities, but not involving any minus signs. Expressed as identities of in the ring of symmetric functionSymmetric functionIn algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
s, they read
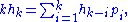
valid for all k ≥ 1. Contrary to Newton's identities,the left-hand sides do not become zero for large k, and the right hand sides contain ever more nonzero terms. For the first few values of k one has
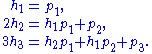
These relations can be justified by an argument analoguous to the one by comparing coefficients in power series given above, based in this case on the generating function identity
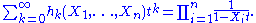
The other proofs given above of Newton's identities cannot be easily adapted to prove these variants of those identities.
Expressing elementary symmetric polynomials in terms of power sums
A mentioned, Newton's identities can be used to recursively express elementary symmetric polynomials in terms of power sums. Doing so requires the introduction of integer denominators, so it can be done in the ring ΛQ of symmetric functions with rational coefficients:
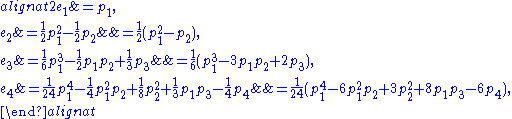
and so forth. Applied to a monic polynomial these formulae express the coefficients in terms of the power sums of the roots: replace each ei by ai and each pk by ψk.
Expressing complete homogeneous symmetric polynomials in terms of power sums
The analogous relations involving complete homogeneous symmetric polynomials can be similarly developed, giving equations
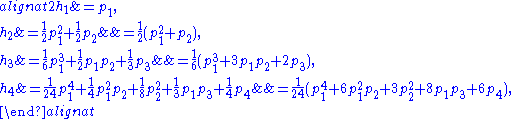
and so forth, in which there are only plus signs. These expressions correspond exactly to the cycle indexCycle indexIn mathematics, and in particular in the field of combinatorics, cycle indices are used in combinatorial enumeration when symmetries are to be taken into account...
polynomials of the symmetric groups, if one interprets the power sums pi as indeterminates: the coefficient in the expression for hk of any monomial p1m1p2m2…plml is equal to the fraction of all permutations of k that have m1 fixed points, m2 cycles of length 2, …, and ml cycles of length l. Explicitly, this coefficient can be written as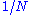 where
where 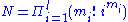 ; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
Expressing power sums in terms of elementary symmetric polynomials
One may also use Newton's identities to express power sums in terms of symmetric polynomials, which does not introduce denominators: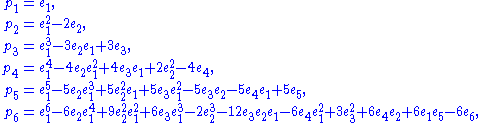
giving ever longer expressions that do not seem to follow any simple pattern. By consideration of the relations used to obtain these expressions, it can however be seen that the coefficient of some monomial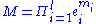 in the expression for
in the expression for 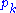 has the same sign as the coefficient of the corresponding product
has the same sign as the coefficient of the corresponding product 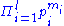 in the expression for
in the expression for 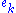 described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficient of
described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficient of 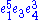 in the expression for p20 will be
in the expression for p20 will be 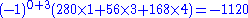 , since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
, since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
Expressing power sums in terms of complete homogeneous symmetric polynomials
Finally one may use the variant identities involving complete homogeneous symmetric polynomials similarly to express power sums in term of them: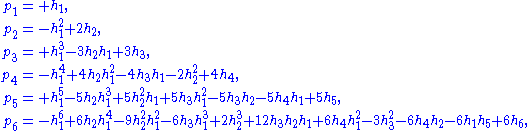
and so on. Apart from the replacement of each ei by the corresponding hi, the only change with respect to the previous family of identities is in the signs of the terms, which in this case depend just on the number of factors present: the sign of the monomial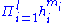 is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
Expressions as determinants
One can obtain explicit formulas for the above expressions in the form of determinants, by considering the first n of Newton's identities (or it counterparts for the complete homogeneous polynomials) as linear equations in which the elementary symmetric functions are known and the power sums are unknowns (or vice versa), and apply Cramer's ruleCramer's ruleIn linear algebra, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution...
to find the solution for the final unknown. For instance taking Newton's identities in the form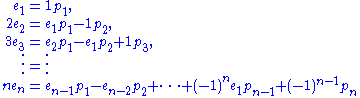
we consider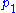 ,
, 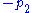 ,
, 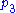 , ...,
, ..., 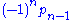 and
and 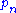 as unknowns, and solve for the final one, giving
as unknowns, and solve for the final one, giving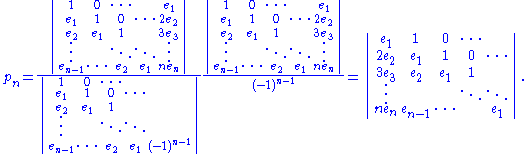
Solving for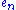 instead of for
instead of for 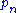 is similar, as the analogous computations for the complete homogeneous symmetric polynomials; in each case the details are slightly messier than the final results, which are (Macdonald 1979, p. 20):
is similar, as the analogous computations for the complete homogeneous symmetric polynomials; in each case the details are slightly messier than the final results, which are (Macdonald 1979, p. 20):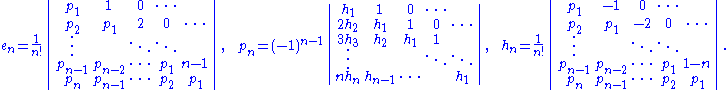
Note that the use of determinants makes that formula for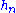 has additional minus signs with respect to the one for
has additional minus signs with respect to the one for 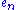 , while the situation for the expanded form given earlier is opposite. As remarked in (Littelwood 1950, p. 84) one can alternatively obtain the formula for
, while the situation for the expanded form given earlier is opposite. As remarked in (Littelwood 1950, p. 84) one can alternatively obtain the formula for 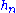 by taking the permanentPermanentThe permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix...
by taking the permanentPermanentThe permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix...
of the matrix for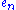 instead of the determinant, and more generally an expression for any Schur polynomialSchur polynomialIn mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
instead of the determinant, and more generally an expression for any Schur polynomialSchur polynomialIn mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
can be obtained by taking the corresponding immanant of this matrix.
Derivation of the identities
Each of Newton's identities can easily be checked by elementary algebra; however, their validity in general needs a proof. Here are some possible derivations
From the special case n = k
One can obtain the k-th Newton identity in k variables by substitution into
as follows. Substituting xj for t gives
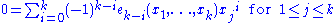
Summing over all j gives
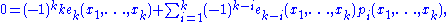
where the terms for i = 0 were taken out of the sum because p0 is (usually) not defined. This equation immediately gives the k-th Newton identity in k variables. Since this is an identity of symmetric polynomials (homogeneous) of degree k, its validity for any number of variables follows from its validity for k variables. Concretely, the identities in n < k variables can be deduced by setting k − n variables to zero. The k-th Newton identity in n > k variables contains more terms on both sides of the equation than the one in k variables, but its validity will be assured if the coefficients of any monomial match. Because no individual monomial involves more than k of the variables, the monomial will survive the substitution of zero for some set of n − k (other) variables, after which the equality of coefficients is one that arises in the k-th Newton identity in k (suitably chosen) variables.
Comparing coefficients in series
A derivation can be given by formal manipulations based on the basic relation
linking roots and coefficients of a monic polynomial. However, to facilitate the manipulations one first "reverses the polynomials" by substituting 1/t for t and then multiplying both sides by tn to remove negative powers of t, giving
Swapping sides and expressing the ai as the elementary symmetric polynomials they stand for gives the identity
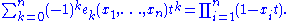
One differentiates both sides with respect to t, and then (for convenience) multiplies by t, to obtain

where the polynomial on the right hand side was first rewritten as a rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
in order to be able to factor out a product from of the summation, then the fraction in the summand was developed as a series in t, and finally the coefficient of each t j was collected, giving a power sum. (The series in t is a formal power series, but may alternatively be thought of as a series expansion for t sufficiently close to 0, for those more comfortable with that; in fact one is not interested in the function here, but only in the coefficients of the series.) Comparing coefficients of tk on both sides one obtains
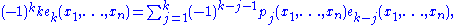
which gives the k-th Newton identity.
As a telescopic sum of symmetric function identities
The following derivation, given essentially in (Mead, 1992), is formulated in the ring of symmetric functions for clarity (all identities are independent of the number of variables). Fix some k > 0, and define the symmetric function r(i) for 2 ≤ i ≤ k as the sum of all distinct monomialMonomialIn mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s of degree k obtained by multiplying one variable raised to the power i with k − i distinct other variables (this is the monomial symmetric function mγ where γ is a hook shape (i,1,1,…1)). In particular r(k) = pk; for r(1) the description would amount to that of ek, but this case was excluded since here monomials no longer have any distinguished variable. All products piek−i can be expressed in terms of the r(j) with the first and last case being somewhat special. One has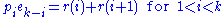
since each product of terms on the left involving distinct variables contributes to r(i), while those where the variable from pi already occurs among the variables of the term from ek−i contributes to r(i + 1), and all terms on the right are so obtained exactly once. For i = k one multiplies by e0 = 1, giving trivially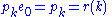 .
.
Finally the product p1ek−1 for i = 1 gives contributions to r(i + 1) = r(2) like for other values i < k, but the remaining contributions produce k times each monomial of ek, since any on of the variables may come from the factor p1; thus .
.
The k-th Newton identity is now obtained by taking the alternating sum of these equations, in which all terms of the form r(i) cancel out.
See also
- Power sum symmetric polynomialPower sum symmetric polynomialIn mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric...
- Elementary symmetric polynomialElementary symmetric polynomialIn mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
- Symmetric functionSymmetric functionIn algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
- Fluid solutionFluid solutionIn general relativity, a fluid solution is an exact solution of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a fluid....
s, an article giving an application of Newton's identities to computing the characteristic polynomial of the Einstein tensorEinstein tensorIn differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
in the case of a perfect fluidPerfect fluidIn physics, a perfect fluid is a fluid that can be completely characterized by its rest frame energy density ρ and isotropic pressure p....
, and similar articles on other types of exact solutions in general relativityExact solutions in general relativityIn general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
.
External links
- Newton–Girard formulas on MathWorld
- A Matrix Proof of Newton's Identities in Mathematics Magazine
-
-