Cycle index
Encyclopedia
In mathematics
, and in particular in the field of combinatorics
, cycle indices are used in combinatorial enumeration when symmetries are to be taken into account. This is particularly important in species theory
.
Each permutation π of a finite set of objects partitions
that set into cycle
s; the cycle index monomial of π is a monomial
in variables a1, a2, … that describes the type of this partition (the cycle type of π): the exponent of ai is the number of cycles of π of size i. The cycle index polynomial of a permutation group
is the average of the cycle index monomials of its elements. The terms cycle index and cycle indicator are also used, both for the cycle index monomial of a permutation and for the cycle index polynomial of a group.
Knowing the cycle index polynomial of a permutation group, one can enumerate equivalence classes of objects that arise when the group acts on a set of slots being filled with objects described by a generating function
. This is the most common application and it uses the Pólya enumeration theorem.
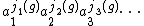
over all permutations g of the group, where jk(g) is the number of cycles of length k in the disjoint cycle decomposition of g.
More formally, let G be a permutation group of order m and degree n.
Every permutation g in G has a unique decomposition into disjoint cycles, say
c1 c2 c3 ...
Let the length of a cycle c be denoted by |c|.
Now let jk(g) be the number of cycles of g of length k, where
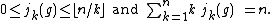
We associate to g the monomial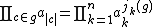
in the variables a1, a2, ... an.
Then the cycle index Z(G) of G is given by
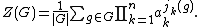
The question of what the cycle structure of a random permutation looks like is an important question in the analysis of algorithms
. An overview of the most important results may be found at random permutation statistics
.
here.
The cyclic group C3 = {e,(1 2 3),(1 3 2)} consists of the identity and two 3-cycles. Thus its cycle index is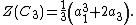
The symmetric group S3 has the elements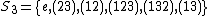
and its cycle index is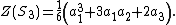
The cyclic group C6 contains the six permutations
and its cycle index is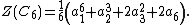
No vertices are permuted, and no edges; the contribution is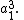
These fix one edge (the one not incident on the vertex) and exchange the remaining two;
the contribution is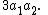
These create a cycle of three edges; the contribution is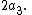
The cycle index of the group G of edge permutations induced by vertex permutations
from S3 is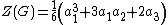
It happens that K3 is its own dual and hence the edge permutation group induced by the vertex permutation group is the same as the vertex permutation group, namely S3 and the cycle index is Z(S3). This is not the case for graphs on more than three vertices, where the vertex permutation group has degree n and the edge permutation group has degree n(n − 1)/2. For n > 3 we have n(n − 1)/2 > n. We will see an example in the next section.
This permutation maps all vertices (and hence, edges) to themselves and the contribution is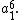
These permutations preserve the edge that connects the two vertices as well as the edge that connects the two vertices not exchanged. The remaining edges form two two-cycles and the contribution is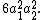
These permutations create two three-cycles of edges, one containing those not incident on the vertex, and another one containing those incident on the vertex; the contribution is
These permutations preserve the two edges that connect the two pairs. The remaining edges form two two-cycles and the contribution is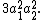
These permutations create a four-cycle of edges (those that lie on the cycle) and exchange the remaining two edges; the contribution is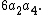
Note that we may visualize the types of permutations as symmetries of a regular tetrahedron
. This yields the following description of the permutation types.
We have computed the cycle index of the edge permuation group G of graphs on four vertices and it is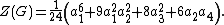
Consider an ordinary cube in three-space and its automorphisms under rotations, which form a group,
call it C. It permutes the six faces of the cube.
(We could also consider edge permutations or vertex permutations.)
There are twenty-four automorphisms. We will classify them all and compute the cycle index of C.
There is one such permutation and its contribution is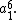
We rotate about the axis passing through the centers of the face and the face opposing it.
This will fix the face and the face opposing it and create a four-cycle of the faces parallel to the axis of rotation. The contribution is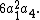
We rotate about the same axis as in the previous case, but now there is no four cycle of the faces parallel to the axis, but rather two two-cycles. The contribution is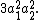
This time we rotate about the axis passing through two opposite vertices (the endpoints of a main diagonal).
This creates two three-cycles of faces (the faces incident on the same vertex form a cycle). The contribution is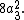
These edge rotations rotate about the axis that passes through the midpoints of opposite edges not incident on the same face and parallel to each other and exchanges the two faces that are incident on the first edge, the two faces incident on the second edge, and the two faces that share two vertices but no edge with the two edges, i.e. there are three two-cycles and the contribution is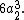
The conclusion is that the cycle index of the group C is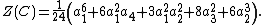
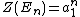
is the group of rotations of n elements round a circle.
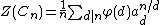
This formula is easily verified for powers of primes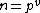
, where we use the fact that the cyclic group is isomorphic to the group generated by 
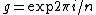with multiplication being the group operation. It is thus readily apparent that the order of 
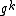is 
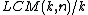or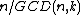 
. The possible values of the order are 
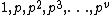according to whether 
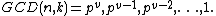But the number of solutions from the interval 
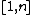to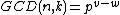 
is one when 
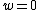and 
otherwise, so that the number of elements of each order is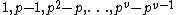 
, giving
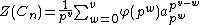
which is the formula from above (where we have taken into account that a permutation of order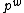
splits into 
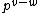cycles, each of which is obtained by a single application of 
).
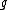is like the cyclic group
, but also includes reflections.
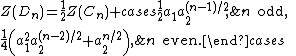
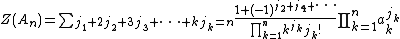
Sn is given by the formula: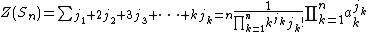
that can be also stated in terms of complete Bell polynomials: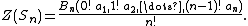
This formula is obtained by counting how many times a given permutation shape can occur. There are three steps: first partition the set of n labels into subsets, where there are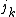
subsets of size k. Every such subset generates 
cycles of length k. But we do not distinguish between cycles of the same size, i.e. they are permuted by 
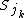. This yields
There is a useful recursive formula for the cycle index of the symmetric group.
Set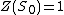
and consider the size l of the cycle that contains n,
where
There are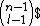
ways to choose
the remaining
elements of the cycle and every such choice generates
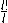different cycles.
This yields the recurrence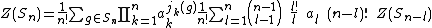
or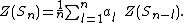
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and in particular in the field of combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, cycle indices are used in combinatorial enumeration when symmetries are to be taken into account. This is particularly important in species theory
Combinatorial species
In combinatorial mathematics, the theory of combinatorial species is an abstract, systematic method for analysing discrete structures in terms of generating functions. Examples of discrete structures are graphs, permutations, trees, and so on; each of these has an associated generating function...
.
Each permutation π of a finite set of objects partitions
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
that set into cycle
Cycle (mathematics)
In mathematics, and in particular in group theory, a cycle is a permutation of the elements of some set X which maps the elements of some subset S to each other in a cyclic fashion, while fixing all other elements...
s; the cycle index monomial of π is a monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
in variables a1, a2, … that describes the type of this partition (the cycle type of π): the exponent of ai is the number of cycles of π of size i. The cycle index polynomial of a permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
is the average of the cycle index monomials of its elements. The terms cycle index and cycle indicator are also used, both for the cycle index monomial of a permutation and for the cycle index polynomial of a group.
Knowing the cycle index polynomial of a permutation group, one can enumerate equivalence classes of objects that arise when the group acts on a set of slots being filled with objects described by a generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
. This is the most common application and it uses the Pólya enumeration theorem.
Definition
The cycle index of a permutation group G is the average of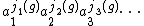over all permutations g of the group, where jk(g) is the number of cycles of length k in the disjoint cycle decomposition of g.
More formally, let G be a permutation group of order m and degree n.
Every permutation g in G has a unique decomposition into disjoint cycles, say
c1 c2 c3 ...
Let the length of a cycle c be denoted by |c|.
Now let jk(g) be the number of cycles of g of length k, where
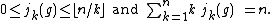
We associate to g the monomial
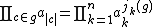
in the variables a1, a2, ... an.
Then the cycle index Z(G) of G is given by
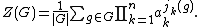
The question of what the cycle structure of a random permutation looks like is an important question in the analysis of algorithms
Analysis of algorithms
To analyze an algorithm is to determine the amount of resources necessary to execute it. Most algorithms are designed to work with inputs of arbitrary length...
. An overview of the most important results may be found at random permutation statistics
Random permutation statistics
The statistics of random permutations, such as the cycle structure of a random permutation are of fundamental importance in the analysis of algorithms, especially of sorting algorithms, which operate on random permutations. Suppose, for example, that we are using quickselect to select a random...
.
Examples
Basic examples of disjoint cycle decompositions may be foundhere.
The cyclic group C3 = {e,(1 2 3),(1 3 2)} consists of the identity and two 3-cycles. Thus its cycle index is
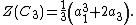
The symmetric group S3 has the elements
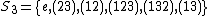
and its cycle index is
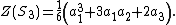
The cyclic group C6 contains the six permutations
[1 2 3 4 5 6] = (1)(2)(3)(4)(5)(6)
[2 3 4 5 6 1] = (1 2 3 4 5 6)
[3 4 5 6 1 2] = (1 3 5)(2 4 6)
[4 5 6 1 2 3] = (1 4)(2 5)(3 6)
[5 6 1 2 3 4] = (1 5 3)(2 6 4)
[6 1 2 3 4 5] = (1 6 5 4 3 2).
and its cycle index is
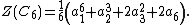
Case study: edge permutation group of graphs on three vertices
Consider graphs on three vertices. Every permutation in the group S3 of vertex permutations induces an edge permutation and we want to compute the cycle index of the latter group. These are the permutations:- The identity.
No vertices are permuted, and no edges; the contribution is
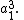
- Three reflections in an axis passing through a vertex and the midpoint of the opposite edge.
These fix one edge (the one not incident on the vertex) and exchange the remaining two;
the contribution is
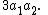
- Two rotations, one clockwise, the other counterclockwise.
These create a cycle of three edges; the contribution is
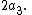
The cycle index of the group G of edge permutations induced by vertex permutations
from S3 is
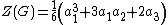
It happens that K3 is its own dual and hence the edge permutation group induced by the vertex permutation group is the same as the vertex permutation group, namely S3 and the cycle index is Z(S3). This is not the case for graphs on more than three vertices, where the vertex permutation group has degree n and the edge permutation group has degree n(n − 1)/2. For n > 3 we have n(n − 1)/2 > n. We will see an example in the next section.
Case study: edge permutation group of graphs on four vertices
We compute the cycle index of the edge permutation group for graphs on four vertices. The process is entirely analogous to the three-vertex case. These are the vertex permutations and the edge permutations that they induce:- The identity.
This permutation maps all vertices (and hence, edges) to themselves and the contribution is
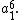
- Six permutations that exchange two vertices.
These permutations preserve the edge that connects the two vertices as well as the edge that connects the two vertices not exchanged. The remaining edges form two two-cycles and the contribution is
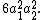
- Eight permutations that fix one vertex and produce a three-cycle for the three vertices not fixed.
These permutations create two three-cycles of edges, one containing those not incident on the vertex, and another one containing those incident on the vertex; the contribution is
- Three permutations that exchange two vertex pairs at the same time.
These permutations preserve the two edges that connect the two pairs. The remaining edges form two two-cycles and the contribution is
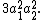
- Six permutations that rotate the vertices along a four-cycle.
These permutations create a four-cycle of edges (those that lie on the cycle) and exchange the remaining two edges; the contribution is
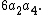
Note that we may visualize the types of permutations as symmetries of a regular tetrahedron
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
. This yields the following description of the permutation types.
- The identity.
- Reflection in the plane that contains one edge and the midpoint of the edge opposing it.
- Rotation by 120 degrees about the axis passing through a vertex and the midpoint of the opposite face.
- Rotation by 180 degrees about the axis connecting the midpoints of two opposite edges.
- Six rotoreflections by 90 degrees.
We have computed the cycle index of the edge permuation group G of graphs on four vertices and it is
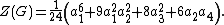
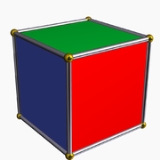
Case study: face permutations of a cube
call it C. It permutes the six faces of the cube.
(We could also consider edge permutations or vertex permutations.)
There are twenty-four automorphisms. We will classify them all and compute the cycle index of C.
- The identity.
There is one such permutation and its contribution is
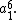
- Six 90-degree face rotations.
We rotate about the axis passing through the centers of the face and the face opposing it.
This will fix the face and the face opposing it and create a four-cycle of the faces parallel to the axis of rotation. The contribution is
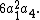
- Three 180-degree face rotations.
We rotate about the same axis as in the previous case, but now there is no four cycle of the faces parallel to the axis, but rather two two-cycles. The contribution is
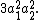
- Eight 120-degree vertex rotations.
This time we rotate about the axis passing through two opposite vertices (the endpoints of a main diagonal).
This creates two three-cycles of faces (the faces incident on the same vertex form a cycle). The contribution is
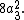
- Six 180-degree edge rotations.
These edge rotations rotate about the axis that passes through the midpoints of opposite edges not incident on the same face and parallel to each other and exchanges the two faces that are incident on the first edge, the two faces incident on the second edge, and the two faces that share two vertices but no edge with the two edges, i.e. there are three two-cycles and the contribution is
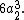
The conclusion is that the cycle index of the group C is
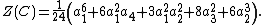
Identity group En
This group contains one permutation that fixes every element.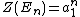Cyclic group Cn
Cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
is the group of rotations of n elements round a circle.
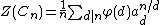
This formula is easily verified for powers of primes
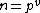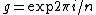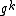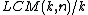, where we use the fact that the cyclic group is isomorphic to the group generated by with multiplication being the group operation. It is thus readily apparent that the order of is or 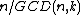. The possible values of the order are 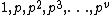according to whether 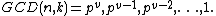But the number of solutions from the interval 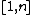to 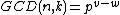is one when 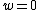and otherwise, so that the number of elements of each order is 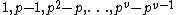, giving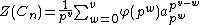which is the formula from above (where we have taken into account that a permutation of order
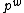splits into 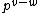cycles, each of which is obtained by a single application of 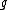).Dihedral group Dn
Dihedral groupDihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
is like the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
, but also includes reflections.
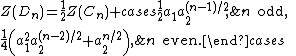
The alternating group An
The alternating group includes all even n! permutations of n elements.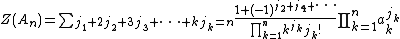The symmetric group Sn
The cycle index of the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn is given by the formula:
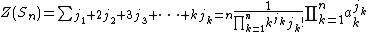
that can be also stated in terms of complete Bell polynomials:
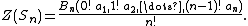
This formula is obtained by counting how many times a given permutation shape can occur. There are three steps: first partition the set of n labels into subsets, where there are
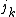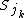subsets of size k. Every such subset generates cycles of length k. But we do not distinguish between cycles of the same size, i.e. they are permuted by . This yieldsThere is a useful recursive formula for the cycle index of the symmetric group.
Set
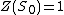and consider the size l of the cycle that contains n,where
There are
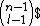ways to choosethe remaining
elements of the cycle and every such choice generates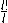 different cycles.This yields the recurrence
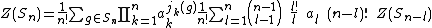
or
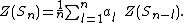
External links
- Marko Riedel, Pólya's enumeration theorem and the symbolic method.