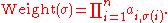Permanent
Encyclopedia
The permanent of a square matrix in linear algebra
, is a function of the matrix similar to the determinant
. The permanent, as well as the determinant, is a polynomial in the entries of the matrix. Both permanent and determinant are special cases of a more general function of a matrix called the immanant.
The sum here extends over all elements σ of the symmetric group
Sn, i.e. over all permutation
s of the numbers 1, 2, ..., n.
For example (2×2 matrix),
The definition of the permanent of A differs from that of the determinant
of A in that the signatures of the permutations are not taken into account. If one views the permanent as a map that takes n vectors as arguments, then it is a multilinear map and it is symmetric (meaning that any order of the vectors results in the same permanent). A formula similar to Laplace's for the development of a determinant along a row or column is also valid for the permanent; all signs have to be ignored for the permanent.
The permanent of a matrix A is denoted per A, perm A, or Per A, sometimes with parentheses around the argument. In his monograph, uses Per(A) for the permanent of rectangular matrices, and uses per(A) when A is a square matrix. uses the notation
.
The word, permanent originated with as “fonctions symétriques permanentes” for a related type of functions, and was used by in the modern, more specific, sense.
and in treating boson Green's functions in quantum field theory
. However, it has two graph-theoretic interpretations: as the sum of weights of cycle cover
s of a directed graph
, and as the sum of weights of perfect matchings in a bipartite graph
.
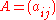can be viewed as the adjacency matrix
of a directed graph, with
representing the weight of the edge from vertex i to vertex j.
A cycle cover
of a weighted directed graph is a collection of vertex-disjoint directed cycles in the graph that covers all nodes in the graph. Thus, each vertex i in the graph has a unique "successor"
in the cycle cover, and 
is a permutation
on
where n is the number of vertices in the graph. Conversely, any permutation 
on 
corresponds to a cycle cover in which there is an edge from vertex i to vertex 
for each i.
If the weight of a cycle-cover is defined to be the product of the weights of the edges in each cycle, then
The permanent of an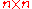
matrix A is defined as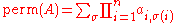
where
is a permutation over 
. Thus the permanent of A is equal to the sum of the weights of all cycle-covers of the graph.
can also be viewed as the biadjacency matrix of a bipartite graph
which has vertices
on one side and 
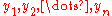on the other side, with 
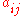representing the weight of the edge from vertex 
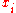to vertex 
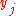. If the weight of a perfect matching 
that matches 
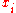to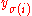 
is defined to be the product of the weights of the edges in the matching, then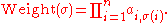
Thus the permanent of A is equal to the sum of the weights of all perfect matchings of the graph.
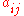to be 1 if there is an edge from vertex i to vertex j, then each nonzero cycle cover has weight 1, and the adjacency matrix has 0-1 entries. Thus the permanent of a 01-matrix is equal to the number of cycle-covers of an unweighted directed graph.
For an unweighted bipartite graph, if we set ai,j = 1 if there is an edge
between the vertices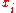
and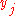 
and ai,j = 0 otherwise, then each perfect matching has weight 1. Thus the number of perfect matchings in G is equal to the permanent of matrix A.
, the matrix aij = 1/n (that is, the uniform matrix) has strictly the smallest permanent. This was conjectured by van der Waeden
, and proved in the late 1970-s independently by Falikman and Egorychev. The proof of Egorychev is an application of the Alexandrov–Fenchel inequality.
, Gaussian elimination cannot be used to compute the permanent. Moreover, computing the permanent of a 0-1 matrix (matrix whose entries are 0 or 1) is #P-complete. Thus, if the permanent can be computed in polynomial time by any method, then FP
= #P
, which is an even stronger statement than P = NP. When the entries of A are nonnegative, however, the permanent can be computed approximately
in probabilistic
polynomial time, up to an error of εM, where M is the value of the permanent and ε > 0 is arbitrary.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, is a function of the matrix similar to the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. The permanent, as well as the determinant, is a polynomial in the entries of the matrix. Both permanent and determinant are special cases of a more general function of a matrix called the immanant.
Definition
The permanent of an n-by-n matrix A = (ai,j) is defined as
The sum here extends over all elements σ of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn, i.e. over all permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of the numbers 1, 2, ..., n.
For example (2×2 matrix),
The definition of the permanent of A differs from that of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of A in that the signatures of the permutations are not taken into account. If one views the permanent as a map that takes n vectors as arguments, then it is a multilinear map and it is symmetric (meaning that any order of the vectors results in the same permanent). A formula similar to Laplace's for the development of a determinant along a row or column is also valid for the permanent; all signs have to be ignored for the permanent.
The permanent of a matrix A is denoted per A, perm A, or Per A, sometimes with parentheses around the argument. In his monograph, uses Per(A) for the permanent of rectangular matrices, and uses per(A) when A is a square matrix. uses the notation
.The word, permanent originated with as “fonctions symétriques permanentes” for a related type of functions, and was used by in the modern, more specific, sense.
Properties and applications
Unlike the determinant, the permanent has no easy geometrical interpretation; it is mainly used in combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and in treating boson Green's functions in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. However, it has two graph-theoretic interpretations: as the sum of weights of cycle cover
Vertex cycle cover
In mathematics, a vertex cycle cover of a graph G is a set of cycles which are subgraphs of G and contain all vertices of G....
s of a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
, and as the sum of weights of perfect matchings in a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
.
Cycle covers
Any square matrix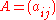 can be viewed as the adjacency matrixAdjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of a directed graph, with
representing the weight of the edge from vertex i to vertex j.A cycle cover
Vertex cycle cover
In mathematics, a vertex cycle cover of a graph G is a set of cycles which are subgraphs of G and contain all vertices of G....
of a weighted directed graph is a collection of vertex-disjoint directed cycles in the graph that covers all nodes in the graph. Thus, each vertex i in the graph has a unique "successor"
in the cycle cover, and is a permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
on
where n is the number of vertices in the graph. Conversely, any permutation on corresponds to a cycle cover in which there is an edge from vertex i to vertex for each i.If the weight of a cycle-cover is defined to be the product of the weights of the edges in each cycle, then
The permanent of an
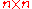matrix A is defined as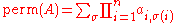where
is a permutation over . Thus the permanent of A is equal to the sum of the weights of all cycle-covers of the graph.Perfect matchings
A square matrix can also be viewed as the biadjacency matrix of a bipartite graphBipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
which has vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
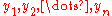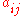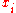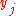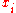on one side and on the other side, with representing the weight of the edge from vertex to vertex . If the weight of a perfect matching that matches to 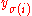is defined to be the product of the weights of the edges in the matching, then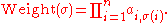Thus the permanent of A is equal to the sum of the weights of all perfect matchings of the graph.
0-1 permanents: counting in unweighted graphs
In an unweighted, directed, simple graph, if we set each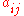 to be 1 if there is an edge from vertex i to vertex j, then each nonzero cycle cover has weight 1, and the adjacency matrix has 0-1 entries. Thus the permanent of a 01-matrix is equal to the number of cycle-covers of an unweighted directed graph.For an unweighted bipartite graph, if we set ai,j = 1 if there is an edge
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
between the vertices
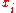and 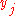and ai,j = 0 otherwise, then each perfect matching has weight 1. Thus the number of perfect matchings in G is equal to the permanent of matrix A.Minimal permanent
Of all the doubly stochastic matricesDoubly stochastic matrix
In mathematics, especially in probability and combinatorics, a doubly stochastic matrix,is a square matrix of nonnegative real numbers, each of whose rows and columns sums to 1...
, the matrix aij = 1/n (that is, the uniform matrix) has strictly the smallest permanent. This was conjectured by van der Waeden
Bartel Leendert van der Waerden
Bartel Leendert van der Waerden was a Dutch mathematician and historian of mathematics....
, and proved in the late 1970-s independently by Falikman and Egorychev. The proof of Egorychev is an application of the Alexandrov–Fenchel inequality.
Computation
The permanent is believed to be more difficult to compute than the determinant. While the determinant can be computed in polynomial time by Gaussian eliminationGaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
, Gaussian elimination cannot be used to compute the permanent. Moreover, computing the permanent of a 0-1 matrix (matrix whose entries are 0 or 1) is #P-complete. Thus, if the permanent can be computed in polynomial time by any method, then FP
FP (complexity)
In computational complexity theory, the complexity class FP is the set of function problems which can be solved by a deterministic Turing machine in polynomial time; it is the function problem version of the decision problem class P...
= #P
Sharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
, which is an even stronger statement than P = NP. When the entries of A are nonnegative, however, the permanent can be computed approximately
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
in probabilistic
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
polynomial time, up to an error of εM, where M is the value of the permanent and ε > 0 is arbitrary.
See also
- DeterminantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
- Bapat–Beg theorem, an application of permanent in order statistics