Natural exponential family
Encyclopedia
In probability
and statistics
, the natural exponential family (NEF) is a class of probability distribution
s that is a special case of an exponential family
(EF). Many common distributions are members of a natural exponential family, and the use of such distributions simplifies the theory and computation of generalized linear models.
. NEF is an exponential family in which the natural parameter η and the natural statistic T(x) are both the identity. A distribution in the exponential family
with parameter θ can be written with probability density function
(PDF)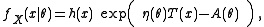
where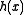
and 
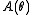are known functions.
A distribution in the natural exponential family with parameter θ can thus be written with PDF
[Note that slightly different notation is used by the originator of the NEF, Carl Morris. Morris uses ω instead of η and ψ instead of A.]
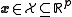, then a natural exponential family of order p has density or mass function of the form: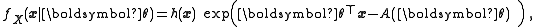
where in this case the parameter
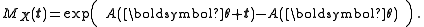
The cumulant generating function is by definition the logarithm of the MGF, so it is
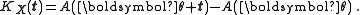
These five examples – Poisson, binomial, negative binomial, normal, and gamma – are a special subset of NEF, called NEF with quadratic variance function (NEF-QVF) because the variance can be written as a quadratic function of the mean. NEF-QVF are discussed below.
Distributions such as the exponential
, chi-squared, Rayleigh, Weibull, Bernoulli, and geometric distributions are special cases of the above five distributions. Many common distributions are either NEF or can be related to the NEF. For example: the chi-squared distribution is a special case of the gamma distribution. The Bernoulli distribution is a binomial distribution with n = 1 trial. The exponential distribution
is a gamma distribution with shape parameter α = 1 (or k = 1 ). The Rayleigh and Weibull distributions can each be written in terms of an exponential distribution.
Some exponential family distributions are not NEF. The lognormal and Beta distribution are in the exponential family, but not the natural exponential family.
The parameterization of most of the above distributions has been written differently than the parameterization commonly used in textbooks and the above linked pages. For example, the above parameterization differs from the parameterization in the linked article in the Poisson case. The two parameterizations are related by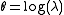
, where λ is the mean parameter, and so that the density may be written as
,
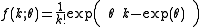for
, so
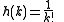, and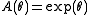 
.
This alternate parameterization can greatly simplify calculations in mathematical statistics
. For example, in Bayesian inference
, a posterior probability
distribution is calculated as the product of two distributions. Normally this calculation requires writing out the probability distribution functions (PDF) and integrating; with the above parameterization, however, that calculation can be avoided. Instead, relationships between distributions can be abstracted due to the below properties of the NEF..
An example of the multivariate case is the multinomial distribution with known number of trials.
The cumulant generating function is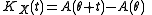
The first cumulant is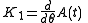
The mean is the first moment and always equal to the first cumulant, so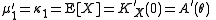
The variance is always the second moment, and it is always related to the first and second cumulants by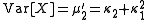
so
The nth cumulant is
2. Natural exponential families (NEF) are closed under convolution.
Given independent identically distributed (iid)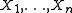
with distribution from an NEF, then 
is an NEF, although not necessarily the original NEF. This follows from the properties of the cumulant generating function.
3. The variance function for random variables with an NEF distribution can be written in terms of the mean.
4. The first two moments of a NEF distribution uniquely characterize the distribution.
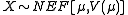
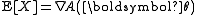and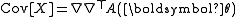 
where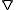
is the gradient
and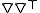
is the Hessian
.
Six NEFs have quadratic variance functions (QVF) in which the variance of the distribution can be written as a quadratic function of the mean. These are called NEF-QVF. The properties of these distributions were first described by Carl Morris
.
1. The normal distribution with fixed variance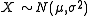
is NEF-QVF because the variance is constant. The variance can be written 
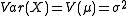, so variance is a degree 0 function of the mean.
2. The Poisson distribution
is NEF-QVF because all Poisson distributions have variance equal to the mean 
, so variance is a linear function of the mean.
3. The Gamma distribution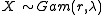
is NEF-QVF because the mean of the Gamma distribution is 
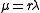and the variance of the Gamma distribution is 
, so the variance is a quadratic function of the mean.
4. The binomial distribution
is NEF-QVF because the mean is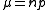 
and the variance is 
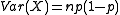which can be written in terms of the mean as
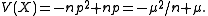
5. The negative binomial distribution
is NEF-QVF because the mean is 
and the variance is
6. The (not very famous) distribution generated by the generalized hyperbolic secant distribution (NEF-GHS) has
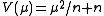and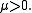 
1. Natural exponential families with quadratic variance functions (NEF-QVF) are closed under convolutions of a linear transformation. That is, a convolution of a linear transformation of an NEF-QVF is also an NEF-QVF, although not necessarily the original one.
Given independent identically distributed (iid)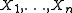
with distribution from a NEF-QVF. A convolution of a linear transformation of an NEF-QVF is also an NEF-QVF.
Let
be the convolution of a linear transformation of X.
The mean of Y is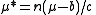
. The variance of Y can be written in terms of the variance function of the original NEF-QVF. If the original NEF-QVF had variance function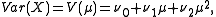
then the new NEF-QVF has variance function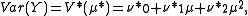
where
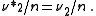
2. Let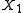
and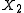 
be independent NEF with the same parameter θ and let 
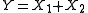. Then the conditional distribution of 
given Y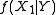 
has quadratic variance in Y if and only if 
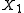and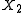 
are NEF-QVF. Examples of conditional distributions 
are the normal, binomial, beta, hypergeometric and geometric distributions, which are not all NEF-QVF.
3. NEF-QVF have conjugate prior
distributions on μ in the Pearson system of distributions (also called the Pearson distribution
although the Pearson system of distributions is actually a family of distributions rather than a single distribution.) Examples of conjugate prior distributions of NEF-QVF distributions are the normal, gamma, reciprocal gamma, beta, F-, and t- distributions. Again, these conjugate priors are not all NEF-QVF.
4. If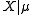
has an NEF-QVF distribution and μ has a conjugate prior distribution then the marginal distributions are well-known distributions.
These properties together with the above notation can simplify calculations in mathematical statistics
that would normally be done using complicated calculations and calculus. This method is the subject of a forthcoming graduate mathematical statistics book by Carl Morris and Joe Blitzstein, who have been teaching the graduate probability and mathematical statistics course using the manuscript since 2006--07.
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the natural exponential family (NEF) is a class of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s that is a special case of an exponential family
Exponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
(EF). Many common distributions are members of a natural exponential family, and the use of such distributions simplifies the theory and computation of generalized linear models.
Probability distribution function (PDF) of the univariate case (scalar domain, scalar parameter)
The natural exponential family (NEF) is a subset of the exponential familyExponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
. NEF is an exponential family in which the natural parameter η and the natural statistic T(x) are both the identity. A distribution in the exponential family
Exponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
with parameter θ can be written with probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(PDF)
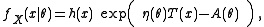
where
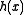and 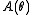are known functions.A distribution in the natural exponential family with parameter θ can thus be written with PDF
[Note that slightly different notation is used by the originator of the NEF, Carl Morris. Morris uses ω instead of η and ψ instead of A.]
Probability distribution function (PDF) of the general case (multivariate domain and/or parameter)
Suppose that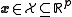, then a natural exponential family of order p has density or mass function of the form: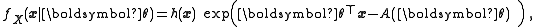where in this case the parameter
Moment and cumulant generating function
A member of a natural exponential family has moment generating function (MGF) of the form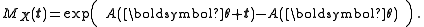The cumulant generating function is by definition the logarithm of the MGF, so it is
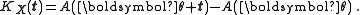
Examples
The five most important univariate cases are:- normal distribution with known variance
- Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
- gamma distribution with known shape parameter α (or k depending on notation set used)
- binomial distribution with known number of trials, n
- negative binomial distributionNegative binomial distributionIn probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
with known
These five examples – Poisson, binomial, negative binomial, normal, and gamma – are a special subset of NEF, called NEF with quadratic variance function (NEF-QVF) because the variance can be written as a quadratic function of the mean. NEF-QVF are discussed below.
Distributions such as the exponential
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
, chi-squared, Rayleigh, Weibull, Bernoulli, and geometric distributions are special cases of the above five distributions. Many common distributions are either NEF or can be related to the NEF. For example: the chi-squared distribution is a special case of the gamma distribution. The Bernoulli distribution is a binomial distribution with n = 1 trial. The exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
is a gamma distribution with shape parameter α = 1 (or k = 1 ). The Rayleigh and Weibull distributions can each be written in terms of an exponential distribution.
Some exponential family distributions are not NEF. The lognormal and Beta distribution are in the exponential family, but not the natural exponential family.
The parameterization of most of the above distributions has been written differently than the parameterization commonly used in textbooks and the above linked pages. For example, the above parameterization differs from the parameterization in the linked article in the Poisson case. The two parameterizations are related by
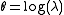, where λ is the mean parameter, and so that the density may be written as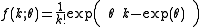,for
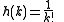, so, and 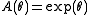.This alternate parameterization can greatly simplify calculations in mathematical statistics
Mathematical statistics
Mathematical statistics is the study of statistics from a mathematical standpoint, using probability theory as well as other branches of mathematics such as linear algebra and analysis...
. For example, in Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
, a posterior probability
Posterior probability
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
distribution is calculated as the product of two distributions. Normally this calculation requires writing out the probability distribution functions (PDF) and integrating; with the above parameterization, however, that calculation can be avoided. Instead, relationships between distributions can be abstracted due to the below properties of the NEF..
An example of the multivariate case is the multinomial distribution with known number of trials.
Properties
The properties of the natural exponential family can be used to simplify calculations involving these distributions.Univariant case
1. The cumulants of an NEF can be calculated as derivatives of the NEF's cumulant generating function. The nth cumulant is the nth derivative with respect to θ of the cumulant generating function.The cumulant generating function is
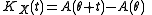
The first cumulant is
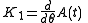
The mean is the first moment and always equal to the first cumulant, so
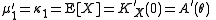
The variance is always the second moment, and it is always related to the first and second cumulants by
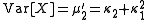
so
The nth cumulant is
2. Natural exponential families (NEF) are closed under convolution.
Given independent identically distributed (iid)
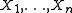with distribution from an NEF, then is an NEF, although not necessarily the original NEF. This follows from the properties of the cumulant generating function.3. The variance function for random variables with an NEF distribution can be written in terms of the mean.
4. The first two moments of a NEF distribution uniquely characterize the distribution.
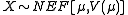
Multivariate case
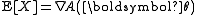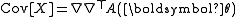
In the multivariate case, the mean vector and covariance matrix are thus: and where
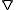is the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
and
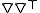is the HessianHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
.
Natural exponential families with quadratic variance functions (NEF-QVF)
A special case of the natural exponential families are those with quadratic variance functions.Six NEFs have quadratic variance functions (QVF) in which the variance of the distribution can be written as a quadratic function of the mean. These are called NEF-QVF. The properties of these distributions were first described by Carl Morris
Carl Morris (statistician)
Carl Morris is a professor in the Statistics Department of Harvard University and spent several years as a researcher for the RAND Corporation working on the RAND Health Insurance Experiment.-Chronology:...
.
The six NEF-QVFs
The six NEF-QVF are written here in increasing complexity of the relationship between variance and mean.1. The normal distribution with fixed variance
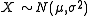is NEF-QVF because the variance is constant. The variance can be written 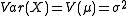, so variance is a degree 0 function of the mean.2. The Poisson distribution
is NEF-QVF because all Poisson distributions have variance equal to the mean , so variance is a linear function of the mean.3. The Gamma distribution
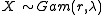is NEF-QVF because the mean of the Gamma distribution is 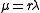and the variance of the Gamma distribution is , so the variance is a quadratic function of the mean.4. The binomial distribution
is NEF-QVF because the mean is 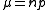and the variance is 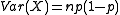which can be written in terms of the mean as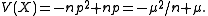5. The negative binomial distribution
is NEF-QVF because the mean is and the variance is6. The (not very famous) distribution generated by the generalized hyperbolic secant distribution (NEF-GHS) has
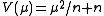and 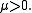Properties of NEF-QVF
The properties of NEF-QVF can simplify calculations that use these distributions.1. Natural exponential families with quadratic variance functions (NEF-QVF) are closed under convolutions of a linear transformation. That is, a convolution of a linear transformation of an NEF-QVF is also an NEF-QVF, although not necessarily the original one.
Given independent identically distributed (iid)
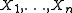with distribution from a NEF-QVF. A convolution of a linear transformation of an NEF-QVF is also an NEF-QVF.Let
be the convolution of a linear transformation of X.The mean of Y is
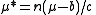. The variance of Y can be written in terms of the variance function of the original NEF-QVF. If the original NEF-QVF had variance function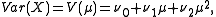then the new NEF-QVF has variance function
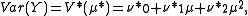
where
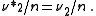
2. Let
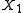and 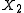be independent NEF with the same parameter θ and let 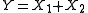. Then the conditional distribution of given Y 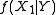has quadratic variance in Y if and only if 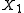and 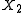are NEF-QVF. Examples of conditional distributions are the normal, binomial, beta, hypergeometric and geometric distributions, which are not all NEF-QVF.3. NEF-QVF have conjugate prior
Conjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
distributions on μ in the Pearson system of distributions (also called the Pearson distribution
Pearson distribution
The Pearson distribution is a family of continuous probability distributions. It was first published by Karl Pearson in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics.- History :...
although the Pearson system of distributions is actually a family of distributions rather than a single distribution.) Examples of conjugate prior distributions of NEF-QVF distributions are the normal, gamma, reciprocal gamma, beta, F-, and t- distributions. Again, these conjugate priors are not all NEF-QVF.
4. If
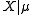has an NEF-QVF distribution and μ has a conjugate prior distribution then the marginal distributions are well-known distributions.These properties together with the above notation can simplify calculations in mathematical statistics
Mathematical statistics
Mathematical statistics is the study of statistics from a mathematical standpoint, using probability theory as well as other branches of mathematics such as linear algebra and analysis...
that would normally be done using complicated calculations and calculus. This method is the subject of a forthcoming graduate mathematical statistics book by Carl Morris and Joe Blitzstein, who have been teaching the graduate probability and mathematical statistics course using the manuscript since 2006--07.