
Multiplication (music)
Encyclopedia
The mathematical operations of multiplication have several applications to music
. Other than its application to the frequency ratios of intervals
(e.g., Just intonation
, and the twelfth root of two in equal temperament
), it has been used in other ways for twelve-tone technique
, and musical set theory. Additionally ring modulation
is an electrical audio process involving multiplication that has been used for musical effect.
A multiplicative operation is a mapping
in which the argument is multiplied (Rahn 1980, 53). Multiplication originated intuitively in interval expansion, including tone row
order number rotation
, for example in the music of Béla Bartók
and Alban Berg
(Schuijer 2008, 77–78). Pitch number rotation, Fünferreihe or "five-series" and Siebenerreihe or "seven-series", was first described by Ernst Krenek
in Über neue Musik (Krenek 1937; Schuijer 2008, 77–78). Princeton-based theorists, including "James K. Randall [1962], Godfrey Winham [1970], and Hubert S. Howe [1967] were the first to discuss and adopt them, not only with regards to twelve-tone series" (Schuijer 2008, 81).
sets, multiplication modulo
12 is a common operation. Dealing with all twelve tones, or a tone row
, there are only a few numbers which one may multiply a row by and still end up with a set of twelve distinct tones. Taking the prime or unaltered form as P0, multiplication is indicated by ,
,  being the multiplicator:
being the multiplicator:
The following table lists all possible multiplications of a chromatic twelve-tone row:
|-
! M
! colspan="12" | M × (0,1,2,3,4,5,6,7,8,9,10,11) mod 12
|-
! width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
|- style="background:#ffdddd"
! 1
| 0 > 1
2
3
4
5
6
7
8
9
10
! 2
| 0 2
4
6
8
10
0
2
4
6
8
! 3
| 0 3
6
9
0
3
6
9
0
3
6
! 4
| 0 4
8
0
4
8
0
4
8
0
4
style="background:#ffdddd"
! 5
| 0
5
10
3
8
1
6
11
4
9
2
! 6
| 0 6
0
6
0
6
0
6
0
6
0
style="background:#ffdddd"
! 7
| 0
7
2
9
4
11
6
1
8
3
10
! 8
| 0 8
4
0
8
4
0
8
4
0
8
! 9
| 0 9
6
3
0
9
6
3
0
9
6
! 10
| 0 10
8
6
4
2
0
10
8
6
4
style="background:#ffdddd"
! 11
| 0
11
10
9
8
7
6
5
4
3
2
Note that only M1, M5, M7, and M11 give a one to one
mapping (a complete set of 12 unique tones). This is because each of these numbers is relatively prime to 12. Also interesting is that the chromatic scale is mapped to the circle of fourths with M5, or fifths with M7, and more generally under M7 all even numbers stay the same while odd numbers are transposed by a tritone
. This kind of multiplication is frequently combined with a transposition
operation. It was first described in print by Herbert Eimert
, under the terms "Quartverwandlung" (fourth transformation) and "Quintverwandlung" (fifth transformation) (Eimert 1950, 29–33), and has been used by the composers Milton Babbitt
(Morris 1997, 238 & 242–43; Winham 1970, 65–66), Robert Morris
(Morris 1997, 238–39 & 243), and Charles Wuorinen
(Hibbard 1969, 157–58). This operation also accounts for certain harmonic transformations in jazz (Morris 1982, 153–54).
Thus multiplication by the two meaningful operations (5 & 7) may be designated with M5(a) and M7(a) or M and IM (Schuijer 2008, 77–78).
(1971,) described an operation he called pitch multiplication, which is somewhat akin to the Cartesian product
of pitch class sets. Given two sets, the result of pitch multiplication will be the set of sums (modulo
12) of all possible pairings of elements between the original two sets. Its definition:

For example, if multiplying a C major chord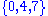 with a dyad containing C,D
with a dyad containing C,D  , the result is:
, the result is:

In this example, a set of 3 pitches multiplied with a set of 2 pitches gives a new set of 3 × 2 pitches. Given the limited space of modulo 12 arithmetic, when using this procedure very often duplicate tones are produced, which are generally omitted. This technique was used most famously in Boulez's 1955 masterpiece Le marteau sans maître
, as well as in his Third Piano Sonata
, Pli selon pli, Eclat (and Eclat multiples), Figures-Doubles-Prisms, Domaines, and Cummings ist der Dichter, as well as the withdrawn choral work, Oubli signal lapidé (1952) (Koblyakov 1990; Heinemann 1993 and 1998).
spoke of the "eight modes" of the twelve-tone series, all mirror forms of one another, the inverse obtained through a horizontal mirror, the retrograde and retrograde-inverse through a vertical mirror, and the "cycle-of-fourths-transform" or Quartverwandlung and "cycle-of-fifths-transform" or Quintverwandlung obtained through a slanting mirror (Eimert 1950, 28–29).
chords are connected by M or IM (multiplication by 5 or multiplication by 7), due to identical entries for 1 and 5 on the APIC vector
(Schuijer 2008, 98n18).
Music
Music is an art form whose medium is sound and silence. Its common elements are pitch , rhythm , dynamics, and the sonic qualities of timbre and texture...
. Other than its application to the frequency ratios of intervals
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
(e.g., Just intonation
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
, and the twelfth root of two in equal temperament
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
), it has been used in other ways for twelve-tone technique
Twelve-tone technique
Twelve-tone technique is a method of musical composition devised by Arnold Schoenberg...
, and musical set theory. Additionally ring modulation
Ring modulation
Ring modulation is a signal-processing effect in electronics, an implementation of amplitude modulation or frequency mixing, performed by multiplying two signals, where one is typically a sine-wave or another simple waveform. It is referred to as "ring" modulation because the analog circuit of...
is an electrical audio process involving multiplication that has been used for musical effect.
A multiplicative operation is a mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
in which the argument is multiplied (Rahn 1980, 53). Multiplication originated intuitively in interval expansion, including tone row
Tone row
In music, a tone row or note row , also series and set, refers to a non-repetitive ordering of a set of pitch-classes, typically of the twelve notes in musical set theory of the chromatic scale, though both larger and smaller sets are sometimes found.-History and usage:Tone rows are the basis of...
order number rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
, for example in the music of Béla Bartók
Béla Bartók
Béla Viktor János Bartók was a Hungarian composer and pianist. He is considered one of the most important composers of the 20th century and is regarded, along with Liszt, as Hungary's greatest composer...
and Alban Berg
Alban Berg
Alban Maria Johannes Berg was an Austrian composer. He was a member of the Second Viennese School with Arnold Schoenberg and Anton Webern, and produced compositions that combined Mahlerian Romanticism with a personal adaptation of Schoenberg's twelve-tone technique.-Early life:Berg was born in...
(Schuijer 2008, 77–78). Pitch number rotation, Fünferreihe or "five-series" and Siebenerreihe or "seven-series", was first described by Ernst Krenek
Ernst Krenek
Ernst Krenek was an Austrian of Czech origin and, from 1945, American composer. He explored atonality and other modern styles and wrote a number of books, including Music Here and Now , a study of Johannes Ockeghem , and Horizons Circled: Reflections on my Music...
in Über neue Musik (Krenek 1937; Schuijer 2008, 77–78). Princeton-based theorists, including "James K. Randall [1962], Godfrey Winham [1970], and Hubert S. Howe [1967] were the first to discuss and adopt them, not only with regards to twelve-tone series" (Schuijer 2008, 81).
Pitch class multiplication modulo 12
When dealing with pitch classPitch class
In music, a pitch class is a set of all pitches that are a whole number of octaves apart, e.g., the pitch class C consists of the Cs in all octaves...
sets, multiplication modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
12 is a common operation. Dealing with all twelve tones, or a tone row
Tone row
In music, a tone row or note row , also series and set, refers to a non-repetitive ordering of a set of pitch-classes, typically of the twelve notes in musical set theory of the chromatic scale, though both larger and smaller sets are sometimes found.-History and usage:Tone rows are the basis of...
, there are only a few numbers which one may multiply a row by and still end up with a set of twelve distinct tones. Taking the prime or unaltered form as P0, multiplication is indicated by
 ,
,  being the multiplicator:
being the multiplicator:
The following table lists all possible multiplications of a chromatic twelve-tone row:
! M
! colspan="12" | M × (0,1,2,3,4,5,6,7,8,9,10,11) mod 12
|-
! width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
| width="20" | 0
|- style="background:#ffdddd"
! 1
| 0 >
! 2
| 0
! 3
| 0
! 4
| 0
! 5
| 0
! 6
| 0
! 7
| 0
! 8
| 0
! 9
| 0
! 10
| 0
! 11
| 0
Note that only M1, M5, M7, and M11 give a one to one
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
mapping (a complete set of 12 unique tones). This is because each of these numbers is relatively prime to 12. Also interesting is that the chromatic scale is mapped to the circle of fourths with M5, or fifths with M7, and more generally under M7 all even numbers stay the same while odd numbers are transposed by a tritone
Tritone
In classical music from Western culture, the tritone |tone]]) is traditionally defined as a musical interval composed of three whole tones. In a chromatic scale, each whole tone can be further divided into two semitones...
. This kind of multiplication is frequently combined with a transposition
Transposition (music)
In music transposition refers to the process, or operation, of moving a collection of notes up or down in pitch by a constant interval.For example, one might transpose an entire piece of music into another key...
operation. It was first described in print by Herbert Eimert
Herbert Eimert
Herbert Eimert was a German music theorist, musicologist, journalist, music critic, editor, radio producer, and composer.-Life:...
, under the terms "Quartverwandlung" (fourth transformation) and "Quintverwandlung" (fifth transformation) (Eimert 1950, 29–33), and has been used by the composers Milton Babbitt
Milton Babbitt
Milton Byron Babbitt was an American composer, music theorist, and teacher. He is particularly noted for his serial and electronic music.-Biography:...
(Morris 1997, 238 & 242–43; Winham 1970, 65–66), Robert Morris
Robert Morris (composer)
Robert Morris is an American composer and music theorist.-Work in music theory:As a music theorist, Morris' work has bridged an important gap between the rigorously academic and the highly experimental. Born in Cheltenham, England in 1943, Morris received his musical education at the Eastman...
(Morris 1997, 238–39 & 243), and Charles Wuorinen
Charles Wuorinen
Charles Peter Wuorinen is a prolific Pulitzer Prize-winning American composer born and living in New York City. His catalog of more than 250 compositions includes works for orchestra, opera, chamber music, as well as solo instrumental and vocal works...
(Hibbard 1969, 157–58). This operation also accounts for certain harmonic transformations in jazz (Morris 1982, 153–54).
Thus multiplication by the two meaningful operations (5 & 7) may be designated with M5(a) and M7(a) or M and IM (Schuijer 2008, 77–78).
Pitch multiplication
Pierre BoulezPierre Boulez
Pierre Boulez is a French composer of contemporary classical music, a pianist, and a conductor.-Early years:Boulez was born in Montbrison, Loire, France. As a child he began piano lessons and demonstrated aptitude in both music and mathematics...
(1971,) described an operation he called pitch multiplication, which is somewhat akin to the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of pitch class sets. Given two sets, the result of pitch multiplication will be the set of sums (modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
12) of all possible pairings of elements between the original two sets. Its definition:

For example, if multiplying a C major chord
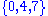 with a dyad containing C,D
with a dyad containing C,D  , the result is:
, the result is:
In this example, a set of 3 pitches multiplied with a set of 2 pitches gives a new set of 3 × 2 pitches. Given the limited space of modulo 12 arithmetic, when using this procedure very often duplicate tones are produced, which are generally omitted. This technique was used most famously in Boulez's 1955 masterpiece Le marteau sans maître
Le marteau sans maître
Le marteau sans maître is a composition by the French composer Pierre Boulez. It is a setting of the surrealist poetry of René Char for alto and six instrumentalists. It was first performed in 1955.-Movements:...
, as well as in his Third Piano Sonata
Piano sonatas (Boulez)
Pierre Boulez has composed three piano sonatas. The First Piano Sonata in 1946, a Second Piano Sonata in 1948, and a Third Piano Sonata was composed in 1955–57 with further elaborations up to at least 1963, though only two of its movements have been published.-First Piano Sonata:Boulez's First...
, Pli selon pli, Eclat (and Eclat multiples), Figures-Doubles-Prisms, Domaines, and Cummings ist der Dichter, as well as the withdrawn choral work, Oubli signal lapidé (1952) (Koblyakov 1990; Heinemann 1993 and 1998).
Mirror form of multiplication
Herbert EimertHerbert Eimert
Herbert Eimert was a German music theorist, musicologist, journalist, music critic, editor, radio producer, and composer.-Life:...
spoke of the "eight modes" of the twelve-tone series, all mirror forms of one another, the inverse obtained through a horizontal mirror, the retrograde and retrograde-inverse through a vertical mirror, and the "cycle-of-fourths-transform" or Quartverwandlung and "cycle-of-fifths-transform" or Quintverwandlung obtained through a slanting mirror (Eimert 1950, 28–29).
Z-relation
Some Z-relatedInterval vector
In musical set theory, an interval vector is an array that expresses the intervallic content of a pitch-class set...
chords are connected by M or IM (multiplication by 5 or multiplication by 7), due to identical entries for 1 and 5 on the APIC vector
Interval vector
In musical set theory, an interval vector is an array that expresses the intervallic content of a pitch-class set...
(Schuijer 2008, 98n18).
Further reading
- Morris, Robert D. 1977. "On the Generation of Multiple-Order-Function Twelve-Tone Rows". Journal of Music Theory 21, no. 2 (Autumn): 238–62.
- Morris, Robert D. 1982–83. "Combinatoriality without the Aggregate". Perspectives of New Music 21, nos. 1 & 2 (Autumn-Winter/Spring-Summer): 432–86.
- Morris, Robert D. 1990. "Pitch-Class Complementation and Its Generalizations". Journal of Music Theory 34, no. 2 (Autumn): 175–245.
- Starr, Daniel V. 1978. "Sets, Invariance, and Partitions." Journal of Music Theory 22, no. 1:1–42.


