
Monte Carlo methods for electron transport
Encyclopedia
The Monte Carlo method for electron transport is a semiclassical Monte Carlo
(MC) approach of modeling semiconductor
transport. Assuming the carrier motion consists of free flights interrupted by scattering mechanisms, a computer is utilized to simulate the trajectories of particles as they move across the device under the influence of an electric field
using classical mechanics
. The scattering events and the duration of particle flight is determined through the use of random numbers.
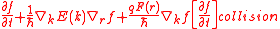

The distribution function
, f, is a dimensionless function which is used to extract all observable of interest and gives a full depiction of electron distribution in both real and k-space
. Further, it physically represents the probability of particle occupation of energy k at position r and time t. In addition, due to being a seven-dimensional integro-differential equation (six dimensions in the phase space and one in time) the solution to the BTE is cumbersome and can be solved in closed analytical form under very special restrictions. Numerically, solution to the BTE is employed using either a deterministic method or a stochastic method. Deterministic method solution is based on a grid-based numerical method such as the spherical harmonics approach, whereas the Monte Carlo is the stochastic approach used to solve the BTE.
processes. This approach is semiclassical for the reason that scattering mechanisms are treated quantum mechanically using the Fermi's Golden Rule
, whereas the transport between scattering events is treated using the classical particle notion. The Monte Carlo model in essence tracks the particle trajectory at each free flight and chooses a corresponding scattering mechanism stochastically. Two of the great advantages of semiclassical Monte Carlo are its capability to provide accurate quantum mechanical treatment of various distinct scattering mechanisms within the scattering terms, and the absence of assumption about the form of carrier distribution in energy or k-space. The semiclassical equation describing the motion of an electron is
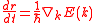
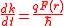
where F is the electric field, E(k) is the energy dispersion relation, and k is the momentum wave vector. To solve the above equation, one needs strong knowledge of the band structure (E(k)). The E(k) relation describes how the particle moves inside the device, in addition to depicting useful information necessary for transport such as the density of states
(DOS) and the particle velocity. A Full-band E(K) relation can be obtained using the semi-empirical pseudopotential method.
the DD scheme with the energy balance equations obtained from the moments of the Boltzmann Transport Equation (BTE). Thus, one may capture and calculate physical details such as carrier heating and the velocity overshoot
effect. Needless to say, an accurate discretization method is required in HD simulation, since the governing equations are strongly coupled and one has to deal with larger number of variables compared to the DD scheme.
(SCE) in transistor structures. Essentially, velocity overshoot is a nonlocal effects of scaled devices, which is related to the experimentally observed increase in current drive and transconductance. As the channel length becomes smaller, the velocity is no longer saturated in the high field region, but it overshoots the predicted saturation velocity. The cause of this phenomenon is that the carrier transit time becomes comparable to the energy relaxation time, and therefore the mobile carriers do not have enough time to reach equilibrium with the applied electric field by scattering in the short channel devices. The summary of simulation results (Illinois Tool: MOCA) with DD and HD model is shown in figure beside. In the figure (a), the case when the field is not high enough to cause the velocity overshoot effect in the whole channel region is shown. Note that at such limit, the data from the DD model fit well to the MC model in the non-overshoot region, but the HD model overestimate the velocity in that region. The velocity overshoot is observed only near the drain junction in the MC data and the HD model fits well in that region. From the MC data, it can be noticed that the velocity overshoot effect is abrupt in the high-field region, which is not properly included in the HD model. For high field conditions as shown in the figure (b) the velocity overshoot effect almost all over the channel and the HD results and the MC results are very close in the channel region.
(k). The band structure is used to compute the movement of carriers under the action of the electric field, scattering rate, and final state after the collision. Silicon band structure and its Brillouin zone are shown in figure below, but there is no analytical expression which satisfies entire Brillouin zone
. By using some approximation, there are two analytical models for band structure, namely the parabolic and the non-parabolic modes.

Because the first derivative vanishes at the band minimum, so the gradient of E(k) is zero at k = 0. Thus,

which yields the definition of the effective mass tensor
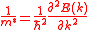
This expression is true for semiconductor which has isotropic effective mass, for instance GaAs. In case of silicon, conduction band minima does not lie at k = 0 and the effect mass depends on the crystallographic orientation of the minimum as
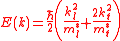
where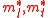 describe longitudinal and transverse effective mass, respectively.
describe longitudinal and transverse effective mass, respectively.
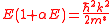
where is a coefficient of non-parabolicity given by
is a coefficient of non-parabolicity given by
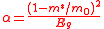
where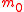 is the electron mass in vacuum, and Eg is the energy gap.
is the electron mass in vacuum, and Eg is the energy gap.
simulate an ensemble of trajectories. This approach is mostly useful to study bulk properties, like the steady state drift velocity as a function of field.
good candidate for super-computation, since one may apply parallelization and vectorization. Also, it is now possible to
perform ensemble averages directly. This approach is suitable for transient simulations.
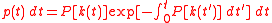
where P[k(t)]dt is the probability that an electron in the state k suffers a collision during the time dt. Because of the complexity of the integral at the exponent, it is impractical to generate stochastic free flights with the distribution of the equation above. In order to overcome this difficulty, people use fictitious “self-scattering” scheme. By doing this, total scattering rate including this self-scattering, is constant and equal to, say, . By random selection, if self-scattering is selected, k′ after the
. By random selection, if self-scattering is selected, k′ after the
collision is same with k and the carrier continues flight without perturbation. Introducing a constant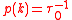 , the above equation reduces to
, the above equation reduces to

Random numbers r can be used very simply to generate stochastic free flights, which duration will then be given by . The computer time used for self-scattering is more than compensated for by the simplification of the calculation of the free-flight duration. To enhance the speed of free flight time calculation, several schemes such as “Constant Technique”, and “Piecewise Technique” are used to minimize the self-scattering events.
. The computer time used for self-scattering is more than compensated for by the simplification of the calculation of the free-flight duration. To enhance the speed of free flight time calculation, several schemes such as “Constant Technique”, and “Piecewise Technique” are used to minimize the self-scattering events.
kinetic theory of collision between two bodies:
Before characterizing scattering mechanisms in greater mathematical details, it is important to note that when running semiconductor Monte Carlo simulations, one has to deal mainly with the following types of scattering events :
These scattering rates are very often derived using the Born approximation
, in which a scattering event is merely a transition between two momentum states of the carrier involved. As discussed in section II-I, the quantum manybody problem arising from the interaction of a carrier with its surrounding environment (phonons, electrons, holes, plasmons, impurities,...) can be reduced to a two-body problem using the quasiparticle approximation, which separates the carrier
of interest from the rest of the crystal. Within these approximations,
Fermi's Golden Rule
gives, to the first order, the transition probability per unit time for a scattering mechanism from a state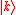 to a state
to a state 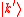 :
:

where H' is the perturbation hamiltonian representing the collision and E and E′ are respectively the initial and final energies of the system constituted of both the carrier and the electron and phonon gas. The Dirac -function stands for the conservation of energy. In addition, the term
-function stands for the conservation of energy. In addition, the term  , generally referred to as the matrix element, mathematically represents an inner product of the initial and final wave functions of the carrier :
, generally referred to as the matrix element, mathematically represents an inner product of the initial and final wave functions of the carrier :

In a crystal lattice, the wavefunctions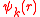 and
and  are
are
simply Bloch waves. When it is possible, analytic expression of the Matrix elements are commonly found by Fourier expanding the hamiltonian
H', as in the case of Impurity
scattering or acoustic phonon scattering.
In the important case of a transition from an energy state E to an energy state E' due to a phonon of wave vector q and frequency , the energy and momentum change is:
, the energy and momentum change is:
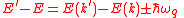
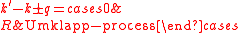
where R is a reciprocal lattice
vector. Umklapp processes (or U-processes) change the momentum of the particle after scattering and are therefore limiting the conduction in semiconductor crystals. Physically, U-processes occur when the final momentum of the particle points out of the first Brillouin zone. Once one knows the scattering probability per unit time from a state k to a state k', it is interesting to determine the scattering rate for a given scattering process. The scattering rate gives the probability per unit time to scatter from a state k to any other state in the reciprocal space. Therefore the scattering rate is

which can be readily used to determine the free flight time and the scattering process as discussed in section 3-3. It is important to note that this scattering rate will be dependent on the band structure of the material (the dependence arises from the matrix elements).
must be randomly chosen. In order to determine the scattering
mechanism, one has to consider all the scattering rates
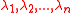 of the mechanisms relevant to the simulation
of the mechanisms relevant to the simulation
as well as the total scattering rate at the time of scattering
Selecting a scattering mechanism then simply results in generating a uniformly distributed random number 0 < r < 1 and referring to the following rules

A computationally efficient approach to selecting the scattering
mechanism consists in adding a “void” scattering mechanism
so that remains constant over time. If a particle is
remains constant over time. If a particle is
scattered according to this mechanism, it will keep its ballistic
trajectory after scattering takes place.
In order to chose a new trajectory, one must first derive the
energy
(or momentum
) of the particle after scattering

where the term accounts for phonon emission or absorption
accounts for phonon emission or absorption
and the term is non-null for inter-valley scattering.
is non-null for inter-valley scattering.
The final energy (and the band structure) directly yield the
modulus of the new momentum k'. At this point on only
needs to chose a new direction (or angle) for the scattered
particle. In some simple cases as phonon scattering
and a
parbolic dispersion relation, the scattering angle is random and
evenly distributed on the sphere of radius k'. Using spherical
coordinates, the process of chosing the angle is equivalent
to randomly picking two angles and
and  . If the angle is
. If the angle is
distributed with a distribution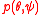 , then for a uniform
, then for a uniform
distribution of angles, the probability
to pick a point of the
sphere is
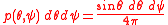
It is possible, in this case, to separate the two vaariables. Integrating over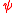 then over
then over  , one finds
, one finds

The two spherical angles can then be chosen, in the uniform case, by generating two random numbers 0 < r1, r2 < 1 such that


has forced physicists to incorporate quantum mechanical issues
in order to acquire a thorough understanding of device
behavior. Simulating the behavior of nano-scale devices necessitates
the use of a full quantum transport
model especially
for cases when the quantum effects cannot be ignored. This
complication, however, can be avoided in the case of practical
devices like the modern day MOSFET
, by employing
quantum corrections within a semi-classical framework. The
semi-classical Monte Carlo model can then be employed to
simulate the device characteristics. The quantum corrections
can be incorporated into a Monte Carlo simulator by simply
introducing a quantum potential term which is superimposed
onto the classical electrostatic potential seen by the simulated
particles. Figure beside pictorially depicts the essential features of
this technique. The various quantum approaches available for
implementation are described in the following subsections.
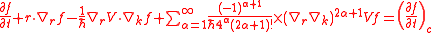
where, k is the crystal momentum, V is the classical potential,
the term on the RHS is the effect of collision,the fourth term
on the LHS represents non-local quantum mechanical effects.
The standard Boltzmann Transport Equation is obtained when
the non-local terms on the LHS disappear in the limit of
slow spatial variations. The simplified (for ) quantum
) quantum
corrected BTE then becomes

where the quantum potential is contained in the term .
.
Feynman and Hibbs in 1965. In this method the effective
potential is derived by calculating the contribution to the path
integral of a particle’s quantum fluctuations around its classical
path. This calculation is undertaken by a variational method
using a trial potential to first order. The effective classical
potential in the average point on each path then becomes
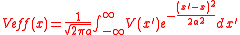
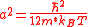
in a simulation with the input being the selfconsistent
electrostatic potential. The exact energy levels and
wavefunctions relating to the electrostatic potential solution
are employed to calculate the quantum potential.
The quantum correction obtained on the bases of this
method can be visualised by the following equation

where Vschr is the quantum correction potential, z is the
direction perpendicular to the interface, nq is the quantum
density from the Schrödinger equation which is equivalent to
the converged Monte Carlo concentration, Vp is the potential
from the Poisson solution, V0 is the arbitrary reference potential
far away from the quantum region such that the correction
goes to null in the region of semi-classical behavior.
Even though the above mentioned potentials for quantum
correction differ in their method of calculation and their basic
assumptions, yet when it comes to their inclusion into Monte
Carlo simulation they are all incorporated the same way.
.org. Quantum correction approach to account for size quantization in narrow channels has been adopted. Below figure shows results of sheet charges and carrier concentration inside a channel of a SOI Device
at different gate biases (0, 0.25, 0.5, 0.75, and 1V).
Monte Carlo
Monte Carlo is an administrative area of the Principality of Monaco....
(MC) approach of modeling semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
transport. Assuming the carrier motion consists of free flights interrupted by scattering mechanisms, a computer is utilized to simulate the trajectories of particles as they move across the device under the influence of an electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
using classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. The scattering events and the duration of particle flight is determined through the use of random numbers.
Boltzmann transport equation
The Boltzmann transport equation model has been the main tool used in the analysis of transport in semiconductors. The BTE equation is given by: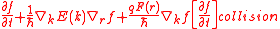

The distribution function
Distribution function
In molecular kinetic theory in physics, a particle's distribution function is a function of seven variables, f, which gives the number of particles per unit volume in phase space. It is the number of particles per unit volume having approximately the velocity near the place and time...
, f, is a dimensionless function which is used to extract all observable of interest and gives a full depiction of electron distribution in both real and k-space
K-space
K-space can refer to:*Another name for the Frequency domain but referring to a spatial rather than temporal frequency*Reciprocal space for the Fourier transform of a spatial function...
. Further, it physically represents the probability of particle occupation of energy k at position r and time t. In addition, due to being a seven-dimensional integro-differential equation (six dimensions in the phase space and one in time) the solution to the BTE is cumbersome and can be solved in closed analytical form under very special restrictions. Numerically, solution to the BTE is employed using either a deterministic method or a stochastic method. Deterministic method solution is based on a grid-based numerical method such as the spherical harmonics approach, whereas the Monte Carlo is the stochastic approach used to solve the BTE.
Monte Carlo method
The semiclassical Monte Carlo method is a statistical method used to yield exact solution to the Boltzmann transport equation which includes complex band structure and scatteringScattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
processes. This approach is semiclassical for the reason that scattering mechanisms are treated quantum mechanically using the Fermi's Golden Rule
Fermi's golden rule
In quantum physics, Fermi's golden rule is a way to calculate the transition rate from one energy eigenstate of a quantum system into a continuum of energy eigenstates, due to a perturbation....
, whereas the transport between scattering events is treated using the classical particle notion. The Monte Carlo model in essence tracks the particle trajectory at each free flight and chooses a corresponding scattering mechanism stochastically. Two of the great advantages of semiclassical Monte Carlo are its capability to provide accurate quantum mechanical treatment of various distinct scattering mechanisms within the scattering terms, and the absence of assumption about the form of carrier distribution in energy or k-space. The semiclassical equation describing the motion of an electron is
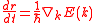
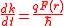
where F is the electric field, E(k) is the energy dispersion relation, and k is the momentum wave vector. To solve the above equation, one needs strong knowledge of the band structure (E(k)). The E(k) relation describes how the particle moves inside the device, in addition to depicting useful information necessary for transport such as the density of states
Density of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
(DOS) and the particle velocity. A Full-band E(K) relation can be obtained using the semi-empirical pseudopotential method.
Hydrodynamic and drift diffusion method
Both drift diffusion (DD) and the hydrodynamic (HD) models can be derived from the moments of the Boltzmann transport equation (BTE) using simplified approximation valid for long channel devices. The DD scheme is a the most classical approach and usually solves the Poisson equation and the continuity equations for carriers considering the drift and diffusion components. In this approach, the charge transit time is assumed to be very large in comparison to the energy relaxation time. On the other hand, the HD method solvesthe DD scheme with the energy balance equations obtained from the moments of the Boltzmann Transport Equation (BTE). Thus, one may capture and calculate physical details such as carrier heating and the velocity overshoot
Velocity overshoot
Velocity overshoot is a result of transit times of a charge carrier going from source to drain being smaller than the time required to emit an optical phonon. The velocity therefore exceeds the saturation velocity, which leads to faster field-effect transistor switching. This notion is utilized...
effect. Needless to say, an accurate discretization method is required in HD simulation, since the governing equations are strongly coupled and one has to deal with larger number of variables compared to the DD scheme.
Comparison of semiclassical models
The accuracy of semiclassical models are compared based on the BTE by investigating how they treat the classical velocity overshoot problem, a key short channel effectShort channel effect
In electronics, a short-channel effect is an effect whereby a MOSFET, in which the channel length is the same order of magnitude as the depletion-layer widths of the source and drain junction, behaves differently from other MOSFETs....
(SCE) in transistor structures. Essentially, velocity overshoot is a nonlocal effects of scaled devices, which is related to the experimentally observed increase in current drive and transconductance. As the channel length becomes smaller, the velocity is no longer saturated in the high field region, but it overshoots the predicted saturation velocity. The cause of this phenomenon is that the carrier transit time becomes comparable to the energy relaxation time, and therefore the mobile carriers do not have enough time to reach equilibrium with the applied electric field by scattering in the short channel devices. The summary of simulation results (Illinois Tool: MOCA) with DD and HD model is shown in figure beside. In the figure (a), the case when the field is not high enough to cause the velocity overshoot effect in the whole channel region is shown. Note that at such limit, the data from the DD model fit well to the MC model in the non-overshoot region, but the HD model overestimate the velocity in that region. The velocity overshoot is observed only near the drain junction in the MC data and the HD model fits well in that region. From the MC data, it can be noticed that the velocity overshoot effect is abrupt in the high-field region, which is not properly included in the HD model. For high field conditions as shown in the figure (b) the velocity overshoot effect almost all over the channel and the HD results and the MC results are very close in the channel region.
Band structure
Band structure describes the relationship between energy(E) and wave vectorWave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
(k). The band structure is used to compute the movement of carriers under the action of the electric field, scattering rate, and final state after the collision. Silicon band structure and its Brillouin zone are shown in figure below, but there is no analytical expression which satisfies entire Brillouin zone
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
. By using some approximation, there are two analytical models for band structure, namely the parabolic and the non-parabolic modes.
Parabolic band structure
For the concept of band structure, parabolic energy bands are generally assumed for simplicity. Electrons reside, at least when close to equilibrium, close to the minima of the E(k) relation. Then the E(k) relation can be extended in a Taylor series as
Because the first derivative vanishes at the band minimum, so the gradient of E(k) is zero at k = 0. Thus,

which yields the definition of the effective mass tensor
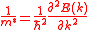
This expression is true for semiconductor which has isotropic effective mass, for instance GaAs. In case of silicon, conduction band minima does not lie at k = 0 and the effect mass depends on the crystallographic orientation of the minimum as
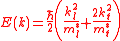
where
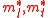 describe longitudinal and transverse effective mass, respectively.
describe longitudinal and transverse effective mass, respectively.Non-parabolic band structure
For higher applied fields, carriers reside above the minimum and the dispersion relation, E(k), does not satisfy the simple parabolic expression described above. This non-parabolicity is generally described by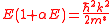
where
 is a coefficient of non-parabolicity given by
is a coefficient of non-parabolicity given by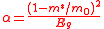
where
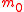 is the electron mass in vacuum, and Eg is the energy gap.
is the electron mass in vacuum, and Eg is the energy gap.Full band structure
For many applications, non-parabolic band structure provides reasonable approximation. However, in case of very high field transport, which requires the better physical model of the full band structure. For full band approach, numerically generated table of E(k) is used. Full band approach for Monte Carlo simulation was first used by Karl Hess at the University of Illinois at Urbana-Champaign. This approach is based on empirical pseudopotential method suggested by Cohen and Bergstresser [18]. Full band approach is computationally expensive, however, following the advancement of the computational power, it can be used as a more general approach.One-particle Monte Carlo
For this type of simulation, one carrier is injected and the motion is tracked in the domain, until it exits through contact. Another carrier is then injected and the process repeated tosimulate an ensemble of trajectories. This approach is mostly useful to study bulk properties, like the steady state drift velocity as a function of field.
Ensemble Monte Carlo
Instead of single carrier, a large ensemble of carriers is simulated at the same time. This procedure is obviously agood candidate for super-computation, since one may apply parallelization and vectorization. Also, it is now possible to
perform ensemble averages directly. This approach is suitable for transient simulations.
Self-consistent ensemble Monte Carlo
This method couples the ensemble Monte Carlo procedure to Poisson’s equation, and is the most suitable for device simulation. Typically, Poisson’s equation is solved at fixed intervals to update the internal field, to reflect the internal redistribution of charge, due to the movement of carriers.Random flight selection
The probability that the electron will suffer its next collision during dt around t is given by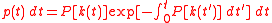
where P[k(t)]dt is the probability that an electron in the state k suffers a collision during the time dt. Because of the complexity of the integral at the exponent, it is impractical to generate stochastic free flights with the distribution of the equation above. In order to overcome this difficulty, people use fictitious “self-scattering” scheme. By doing this, total scattering rate including this self-scattering, is constant and equal to, say,
 . By random selection, if self-scattering is selected, k′ after the
. By random selection, if self-scattering is selected, k′ after thecollision is same with k and the carrier continues flight without perturbation. Introducing a constant
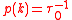 , the above equation reduces to
, the above equation reduces to
Random numbers r can be used very simply to generate stochastic free flights, which duration will then be given by
 . The computer time used for self-scattering is more than compensated for by the simplification of the calculation of the free-flight duration. To enhance the speed of free flight time calculation, several schemes such as “Constant Technique”, and “Piecewise Technique” are used to minimize the self-scattering events.
. The computer time used for self-scattering is more than compensated for by the simplification of the calculation of the free-flight duration. To enhance the speed of free flight time calculation, several schemes such as “Constant Technique”, and “Piecewise Technique” are used to minimize the self-scattering events.General background in solid-state physics
Important charge transport properties of semiconductor devices such as the deviance from Ohm’s law and the saturation of carriers mobility are a direct consequence of scattering mechanisms. It is thus of great importance for a semiconductor device simulation to capture the physics of such mechanisms. The semiconductor Monte Carlo simulation, in this scope, is a very powerful tool for the ease and the precision with which an almost exhaustive array of cattering mechanisms can be included. The duration of the free flights is determined from the scattering rates. At the end of each flight, the appropriate scattering mechanism must be chosen in order to determine the final energy of the scattered carrier, or equivalently, its new momentum and scattering angle. In this sense, one will distinguish two broad types of scattering mechanisms which naturally derive form the classickinetic theory of collision between two bodies:
- • Elastic scattering, where the energy of the particle is conserved after being scattered. Elastic scattering will hence only change the direction of the particle’s momentum. Impurity scattering and surface scattering are, with a fair approximation, two good examples of elastic scattering processes.
- • Inelastic scattering, where energy is transferred between the scattered particle and the scattering center. Electronphonon interactions are essentially inelastic since a phonon of definite energy is either emitted or absorbed by the scattered particle.
Before characterizing scattering mechanisms in greater mathematical details, it is important to note that when running semiconductor Monte Carlo simulations, one has to deal mainly with the following types of scattering events :
- • Acoustic Phonon: The charge carrier exchanges energy with an acoustic mode of the vibration of atoms in the crystal lattice. Acoustic Phonons mainly arise from thermal excitation of the crystal lattice.
- • Polar Optical: The charge carrier exchanges energy with one of the polar optical modes of the crystal lattice. These modes are not present in covalent semiconductors. Optical phonons arise from the vibration against each other of atoms of different types when there is more than one atom in the smallest unit cell, and are usually excited by light.
- • Non-Polar Optical: Energy is exchanged with an optical mode. Non-polar optical phonons must generally be considered in covalent semiconductors and the L-valley of GaAs.
- • Equivalent Intervalley Phonon: Due to the interaction with a phonon, the charge carrier transitions from initial states to final states which belong to different but equivalent valleys. Typically, this type of scattering mechanism describes the transition of an electron from one X-valley to another X-valley, or from one L-valley to another L-valley.
- • Non Equivalent Intervalley Phonon: Involves the transition of a charge carrier between valleys of different types.
- • Piezoelectric Phonon: For low temperatures.
- • Ionized Impurity: Reflects the deviation of a particle from it ballistic trajectory due to Coulomb interaction with an ionized impurity in the crystal lattice. Because the mass of an electron is relatively small in comparison to the one of an impurity, the Coulomb cross section decreases rapidly with the difference of the modulus of momentum between the initial and final state. Therefore impurity scattering events are mostly considered for intravalley scattering, intraband scattering and, to a minor extent, interband scattering.
- • Carrier-Carrier: (electron-electron, hole-hole and electron-hole interactions). When carrier concentration is high, this type of scattering reflects the electrostatic interaction between charge carriers. This problem becomes very quickly computationally intensive with an increasing number of particles in an ensemble simulation. In this scope, Particle-Particle–Particle-Mesh (P3M) algorithms, which distinguish short range and long range interaction of a particle with its surrounding charge gas, have proved efficient in including carrier-carrier interaction in the semiconductor Monte Carlo simulation. Very often, the charge of the carriers is assigned to a grid using a Cloud-in-Cell method, where part of the charge of a given particle is assigned to a given number of closest grid points with a certain weight factor.
- • Plasmon: Reflects the effect of the collective oscillation of the charge carriers on a given particle.
Inclusion of scattering mechanisms in Monte Carlo
A computationally efficient approach to including scattering in Monte Carlo simulation consists in storing the scattering rates of the individual mechanisms in tables. Given the different scattering rates for a precise particle state, one may then randomly select the scattering process at the end of the free flight.These scattering rates are very often derived using the Born approximation
Born approximation
In scattering theory and, in particular in quantum mechanics, the Born approximation consists of taking the incident field in place of the total field as the driving field at each point in the scatterer. Born approximation is named after Max Born, winner of the 1954 Nobel Prize for physics.It is...
, in which a scattering event is merely a transition between two momentum states of the carrier involved. As discussed in section II-I, the quantum manybody problem arising from the interaction of a carrier with its surrounding environment (phonons, electrons, holes, plasmons, impurities,...) can be reduced to a two-body problem using the quasiparticle approximation, which separates the carrier
of interest from the rest of the crystal. Within these approximations,
Fermi's Golden Rule
Fermi's golden rule
In quantum physics, Fermi's golden rule is a way to calculate the transition rate from one energy eigenstate of a quantum system into a continuum of energy eigenstates, due to a perturbation....
gives, to the first order, the transition probability per unit time for a scattering mechanism from a state
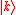 to a state
to a state 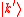 :
:
where H' is the perturbation hamiltonian representing the collision and E and E′ are respectively the initial and final energies of the system constituted of both the carrier and the electron and phonon gas. The Dirac
 -function stands for the conservation of energy. In addition, the term
-function stands for the conservation of energy. In addition, the term  , generally referred to as the matrix element, mathematically represents an inner product of the initial and final wave functions of the carrier :
, generally referred to as the matrix element, mathematically represents an inner product of the initial and final wave functions of the carrier :
In a crystal lattice, the wavefunctions
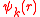 and
and  are
aresimply Bloch waves. When it is possible, analytic expression of the Matrix elements are commonly found by Fourier expanding the hamiltonian
Hamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
H', as in the case of Impurity
scattering or acoustic phonon scattering.
In the important case of a transition from an energy state E to an energy state E' due to a phonon of wave vector q and frequency
 , the energy and momentum change is:
, the energy and momentum change is: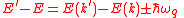
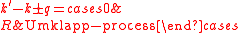
where R is a reciprocal lattice
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
vector. Umklapp processes (or U-processes) change the momentum of the particle after scattering and are therefore limiting the conduction in semiconductor crystals. Physically, U-processes occur when the final momentum of the particle points out of the first Brillouin zone. Once one knows the scattering probability per unit time from a state k to a state k', it is interesting to determine the scattering rate for a given scattering process. The scattering rate gives the probability per unit time to scatter from a state k to any other state in the reciprocal space. Therefore the scattering rate is

which can be readily used to determine the free flight time and the scattering process as discussed in section 3-3. It is important to note that this scattering rate will be dependent on the band structure of the material (the dependence arises from the matrix elements).
Selection of scattering mode and scattered trajectory
At the end of a free flight, a scattering mode and anglemust be randomly chosen. In order to determine the scattering
mechanism, one has to consider all the scattering rates
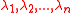 of the mechanisms relevant to the simulation
of the mechanisms relevant to the simulationas well as the total scattering rate at the time of scattering

Selecting a scattering mechanism then simply results in generating a uniformly distributed random number 0 < r < 1 and referring to the following rules

A computationally efficient approach to selecting the scattering
mechanism consists in adding a “void” scattering mechanism
so that
 remains constant over time. If a particle is
remains constant over time. If a particle isscattered according to this mechanism, it will keep its ballistic
trajectory after scattering takes place.
In order to chose a new trajectory, one must first derive the
energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
(or momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
) of the particle after scattering

where the term
 accounts for phonon emission or absorption
accounts for phonon emission or absorptionand the term
 is non-null for inter-valley scattering.
is non-null for inter-valley scattering.The final energy (and the band structure) directly yield the
modulus of the new momentum k'. At this point on only
needs to chose a new direction (or angle) for the scattered
particle. In some simple cases as phonon scattering
Phonon scattering
Phonons can scatter through several mechanisms as they travel through the material. These scattering mechanisms are: Umklapp phonon-phonon scattering, phonon-impurity scattering, phonon-electron scattering, and phonon-boundary scattering...
and a
parbolic dispersion relation, the scattering angle is random and
evenly distributed on the sphere of radius k'. Using spherical
coordinates, the process of chosing the angle is equivalent
to randomly picking two angles
 and
and  . If the angle is
. If the angle isdistributed with a distribution
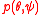 , then for a uniform
, then for a uniformdistribution of angles, the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
to pick a point of the
sphere is
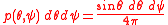
It is possible, in this case, to separate the two vaariables. Integrating over
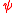 then over
then over  , one finds
, one finds

The two spherical angles can then be chosen, in the uniform case, by generating two random numbers 0 < r1, r2 < 1 such that


Quantum corrections for Monte Carlo simulation
The current trend of scaling down semiconductor deviceshas forced physicists to incorporate quantum mechanical issues
in order to acquire a thorough understanding of device
behavior. Simulating the behavior of nano-scale devices necessitates
the use of a full quantum transport
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
model especially
for cases when the quantum effects cannot be ignored. This
complication, however, can be avoided in the case of practical
devices like the modern day MOSFET
MOSFET
The metal–oxide–semiconductor field-effect transistor is a transistor used for amplifying or switching electronic signals. The basic principle of this kind of transistor was first patented by Julius Edgar Lilienfeld in 1925...
, by employing
quantum corrections within a semi-classical framework. The
semi-classical Monte Carlo model can then be employed to
simulate the device characteristics. The quantum corrections
can be incorporated into a Monte Carlo simulator by simply
introducing a quantum potential term which is superimposed
onto the classical electrostatic potential seen by the simulated
particles. Figure beside pictorially depicts the essential features of
this technique. The various quantum approaches available for
implementation are described in the following subsections.
Wigner-based correction
The Wigner transport equation forms the bases for the Wigner-based quantum correction.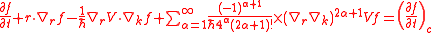
where, k is the crystal momentum, V is the classical potential,
the term on the RHS is the effect of collision,the fourth term
on the LHS represents non-local quantum mechanical effects.
The standard Boltzmann Transport Equation is obtained when
the non-local terms on the LHS disappear in the limit of
slow spatial variations. The simplified (for
 ) quantum
) quantumcorrected BTE then becomes

where the quantum potential is contained in the term
 .
.Effective potential correction
This method of quantum correction was developed byFeynman and Hibbs in 1965. In this method the effective
potential is derived by calculating the contribution to the path
integral of a particle’s quantum fluctuations around its classical
path. This calculation is undertaken by a variational method
using a trial potential to first order. The effective classical
potential in the average point on each path then becomes
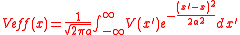
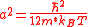
Schrödinger-based correction
This approach involves periodical solving of a Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
in a simulation with the input being the selfconsistent
electrostatic potential. The exact energy levels and
wavefunctions relating to the electrostatic potential solution
are employed to calculate the quantum potential.
The quantum correction obtained on the bases of this
method can be visualised by the following equation

where Vschr is the quantum correction potential, z is the
direction perpendicular to the interface, nq is the quantum
density from the Schrödinger equation which is equivalent to
the converged Monte Carlo concentration, Vp is the potential
from the Poisson solution, V0 is the arbitrary reference potential
far away from the quantum region such that the correction
goes to null in the region of semi-classical behavior.
Even though the above mentioned potentials for quantum
correction differ in their method of calculation and their basic
assumptions, yet when it comes to their inclusion into Monte
Carlo simulation they are all incorporated the same way.
Simulation tool
MOCA is a full-band Monte Carlo Simulator code which is suitable for 2D simulation of silicon devices at NanohubNanohub
nanoHUB.org is science cyberinfrastructure comprising community-contributed resources and geared toward educational applications, professional networking, and interactive simulation tools for nanotechnology...
.org. Quantum correction approach to account for size quantization in narrow channels has been adopted. Below figure shows results of sheet charges and carrier concentration inside a channel of a SOI Device
SOI MOSFET
In electronics, an SOI MOSFET semiconductor device is a Silicon on Insulator MOSFET structure in which a semiconductor layer, e.g. silicon, germanium or the like, is formed above an insulator layer which may be a buried oxide layer formed in a semiconductor substrate. SOI MOSFET devices are...
at different gate biases (0, 0.25, 0.5, 0.75, and 1V).
See also
- Monte Carlo methodMonte Carlo methodMonte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
- Semiconductor deviceSemiconductor deviceSemiconductor devices are electronic components that exploit the electronic properties of semiconductor materials, principally silicon, germanium, and gallium arsenide, as well as organic semiconductors. Semiconductor devices have replaced thermionic devices in most applications...
- Monte Carlo method for photon transportMonte Carlo method for photon transportModeling photon propagation with Monte Carlo methods is a flexible yet rigorous approach to simulate photon transport. In the method, local rules of photon transport are expressed as probability distributions which describe the step size of photon movement between sites of photon-tissue interaction...
- Band structure
- Quantum Monte CarloQuantum Monte CarloQuantum Monte Carlo is a large class of computer algorithms that simulate quantum systems with the idea of solving the quantum many-body problem. They use, in one way or another, the Monte Carlo method to handle the many-dimensional integrals that arise...
- Quasi-Monte Carlo methodQuasi-Monte Carlo methodIn numerical analysis, a quasi-Monte Carlo method is a method for the computation of an integral that is based on low-discrepancy sequences...

