
Moment map
Encyclopedia
In mathematics
, specifically in symplectic geometry, the momentum map (or moment map) is a tool associated with a Hamiltonian action
of a Lie group
on a symplectic manifold
, used to construct conserved quantities for the action. The moment map generalizes the classical notions of linear and angular momentum
. It is an essential ingredient in various constructions of symplectic manifolds, including symplectic (Marsden–Weinstein) quotients, discussed below, and symplectic cut
s and sums
.
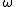 . Suppose that a Lie group G acts on M via symplectomorphism
. Suppose that a Lie group G acts on M via symplectomorphism
s (that is, the action of each g in G preserves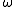 ). Let
). Let 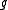 be the Lie algebra
be the Lie algebra
of G,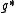 its dual
its dual
, and
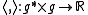
the pairing between the two. Any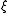 in
in 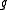 induces a vector field
induces a vector field
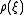 on M describing the infinitesimal action of
on M describing the infinitesimal action of 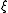 . To be precise, at a point x in M the vector
. To be precise, at a point x in M the vector 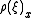 is
is
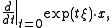
where is the exponential map
is the exponential map
and denotes the G-action on M.. Let
denotes the G-action on M.. Let 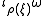 denote the contraction of this vector field with
denote the contraction of this vector field with 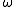 . Because G acts by symplectomorphisms, it follows that
. Because G acts by symplectomorphisms, it follows that 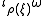 is closed
is closed
for all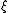 in
in 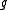 .
.
A moment map for the -action on
-action on 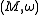 is a map
is a map 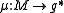 such that
such that

for all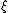 in
in  . Here
. Here 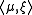 is the function from M to
is the function from M to 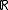 defined by
defined by 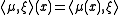 . The moment map is uniquely defined up to an additive constant of integration.
. The moment map is uniquely defined up to an additive constant of integration.
A moment map is often also required to be G-equivariant, where G acts on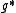 via the coadjoint action. If the group is compact or semisimple, then the constant of integration can always be chosen to make the moment map coadjoint equivariant; however in general the coadjoint action must be modified to make the map equivariant (this is the case for example for the Euclidean group
via the coadjoint action. If the group is compact or semisimple, then the constant of integration can always be chosen to make the moment map coadjoint equivariant; however in general the coadjoint action must be modified to make the map equivariant (this is the case for example for the Euclidean group
).
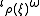 to be exact
to be exact
. In practice it is useful to make an even stronger assumption. The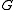 -action is said to be Hamiltonian if and only if the following conditions hold. First, for every
-action is said to be Hamiltonian if and only if the following conditions hold. First, for every 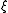 in
in 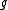 the one-form
the one-form 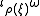 is exact, meaning that it equals
is exact, meaning that it equals 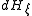 for some smooth function
for some smooth function
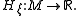
If this holds, then one may choose the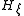 to make the map
to make the map 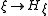 linear. The second requirement for the
linear. The second requirement for the 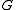 -action to be Hamiltonian is that the map
-action to be Hamiltonian is that the map 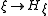 be a Lie algebra homomorphism from
be a Lie algebra homomorphism from 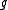 to the algebra of smooth functions on M under the Poisson bracket
to the algebra of smooth functions on M under the Poisson bracket
.
If the action of G on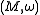 is Hamiltonian in this sense, then a moment map is a map
is Hamiltonian in this sense, then a moment map is a map 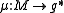 such that writing
such that writing 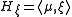 defines a Lie algebra homomorphism
defines a Lie algebra homomorphism 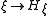 satisfying
satisfying 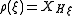 . Here
. Here 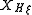 is the vector field of the Hamiltonian
is the vector field of the Hamiltonian 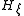 , defined by
, defined by
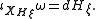
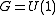 , the Lie algebra dual
, the Lie algebra dual 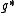 is naturally identified with
is naturally identified with 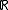 , and the moment map is simply the Hamiltonian function that generates the circle action.
, and the moment map is simply the Hamiltonian function that generates the circle action.
Another classical case occurs when M is the cotangent bundle
of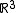 and G is the Euclidean group
and G is the Euclidean group
generated by rotations and translations. That is, G is a six-dimensional group, the semidirect product
of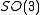 and
and 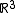 . The six components of the moment map are then the three angular momenta and the three linear momenta.
. The six components of the moment map are then the three angular momenta and the three linear momenta.
Lie group G on the symplectic manifold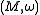 is Hamiltonian, as defined above, with moment map
is Hamiltonian, as defined above, with moment map 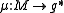 . From the Hamiltonian condition it follows that
. From the Hamiltonian condition it follows that 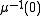 is invariant under G.
is invariant under G.
Assume now that 0 is a regular value of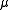 and that G acts freely and properly on
and that G acts freely and properly on 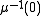 . Thus
. Thus  and its quotient
and its quotient
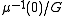 are both manifolds. The quotient inherits a symplectic form from M; that is, there is a unique symplectic form on the quotient whose pullback to
are both manifolds. The quotient inherits a symplectic form from M; that is, there is a unique symplectic form on the quotient whose pullback to 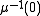 equals the pullback of
equals the pullback of 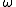 to
to 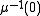 . Thus the quotient is a symplectic manifold, called the Marsden–Weinstein quotient, symplectic quotient or symplectic reduction of M by G and is denoted
. Thus the quotient is a symplectic manifold, called the Marsden–Weinstein quotient, symplectic quotient or symplectic reduction of M by G and is denoted 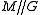 . Its dimension equals the dimension of M minus twice the dimension of G.
. Its dimension equals the dimension of M minus twice the dimension of G.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in symplectic geometry, the momentum map (or moment map) is a tool associated with a Hamiltonian action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
on a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
, used to construct conserved quantities for the action. The moment map generalizes the classical notions of linear and angular momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
. It is an essential ingredient in various constructions of symplectic manifolds, including symplectic (Marsden–Weinstein) quotients, discussed below, and symplectic cut
Symplectic cut
In mathematics, specifically in symplectic geometry, the symplectic cut is a geometric modification on symplectic manifolds. Its effect is to decompose a given manifold into two pieces. There is an inverse operation, the symplectic sum, that glues two manifolds together into one. The symplectic cut...
s and sums
Symplectic sum
In mathematics, specifically in symplectic geometry, the symplectic sum is a geometric modification on symplectic manifolds, which glues two given manifolds into a single new one. It is a symplectic version of connected summation along a submanifold, often called a fiber sum.The symplectic sum is...
.
Formal definition
Let M be a manifold with symplectic form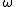 . Suppose that a Lie group G acts on M via symplectomorphism
. Suppose that a Lie group G acts on M via symplectomorphismSymplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
s (that is, the action of each g in G preserves
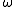 ). Let
). Let 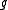 be the Lie algebra
be the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G,
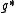 its dual
its dualDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
, and
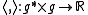
the pairing between the two. Any
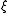 in
in 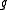 induces a vector field
induces a vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
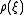 on M describing the infinitesimal action of
on M describing the infinitesimal action of 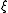 . To be precise, at a point x in M the vector
. To be precise, at a point x in M the vector 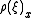 is
is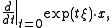
where
 is the exponential map
is the exponential mapExponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
and
 denotes the G-action on M.. Let
denotes the G-action on M.. Let 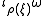 denote the contraction of this vector field with
denote the contraction of this vector field with 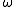 . Because G acts by symplectomorphisms, it follows that
. Because G acts by symplectomorphisms, it follows that 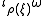 is closed
is closedClosed and exact differential forms
In mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...
for all
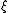 in
in 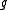 .
.A moment map for the
 -action on
-action on 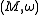 is a map
is a map 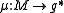 such that
such that
for all
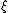 in
in  . Here
. Here 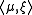 is the function from M to
is the function from M to 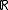 defined by
defined by 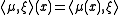 . The moment map is uniquely defined up to an additive constant of integration.
. The moment map is uniquely defined up to an additive constant of integration.A moment map is often also required to be G-equivariant, where G acts on
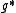 via the coadjoint action. If the group is compact or semisimple, then the constant of integration can always be chosen to make the moment map coadjoint equivariant; however in general the coadjoint action must be modified to make the map equivariant (this is the case for example for the Euclidean group
via the coadjoint action. If the group is compact or semisimple, then the constant of integration can always be chosen to make the moment map coadjoint equivariant; however in general the coadjoint action must be modified to make the map equivariant (this is the case for example for the Euclidean groupEuclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
).
Hamiltonian group actions
The definition of the moment map requires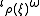 to be exact
to be exactClosed and exact differential forms
In mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...
. In practice it is useful to make an even stronger assumption. The
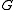 -action is said to be Hamiltonian if and only if the following conditions hold. First, for every
-action is said to be Hamiltonian if and only if the following conditions hold. First, for every 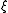 in
in 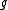 the one-form
the one-form 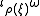 is exact, meaning that it equals
is exact, meaning that it equals 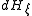 for some smooth function
for some smooth function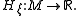
If this holds, then one may choose the
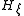 to make the map
to make the map 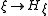 linear. The second requirement for the
linear. The second requirement for the 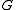 -action to be Hamiltonian is that the map
-action to be Hamiltonian is that the map 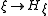 be a Lie algebra homomorphism from
be a Lie algebra homomorphism from 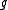 to the algebra of smooth functions on M under the Poisson bracket
to the algebra of smooth functions on M under the Poisson bracketPoisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
.
If the action of G on
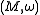 is Hamiltonian in this sense, then a moment map is a map
is Hamiltonian in this sense, then a moment map is a map 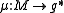 such that writing
such that writing 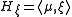 defines a Lie algebra homomorphism
defines a Lie algebra homomorphism 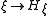 satisfying
satisfying 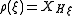 . Here
. Here 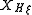 is the vector field of the Hamiltonian
is the vector field of the Hamiltonian 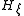 , defined by
, defined by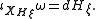
Examples
In the case of a Hamiltonian action of the circle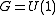 , the Lie algebra dual
, the Lie algebra dual 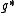 is naturally identified with
is naturally identified with 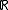 , and the moment map is simply the Hamiltonian function that generates the circle action.
, and the moment map is simply the Hamiltonian function that generates the circle action.Another classical case occurs when M is the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of
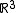 and G is the Euclidean group
and G is the Euclidean groupEuclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
generated by rotations and translations. That is, G is a six-dimensional group, the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of
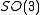 and
and 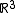 . The six components of the moment map are then the three angular momenta and the three linear momenta.
. The six components of the moment map are then the three angular momenta and the three linear momenta.Symplectic quotients
Suppose that the action of a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Lie group G on the symplectic manifold
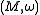 is Hamiltonian, as defined above, with moment map
is Hamiltonian, as defined above, with moment map 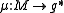 . From the Hamiltonian condition it follows that
. From the Hamiltonian condition it follows that 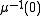 is invariant under G.
is invariant under G.Assume now that 0 is a regular value of
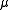 and that G acts freely and properly on
and that G acts freely and properly on 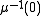 . Thus
. Thus  and its quotient
and its quotientQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
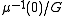 are both manifolds. The quotient inherits a symplectic form from M; that is, there is a unique symplectic form on the quotient whose pullback to
are both manifolds. The quotient inherits a symplectic form from M; that is, there is a unique symplectic form on the quotient whose pullback to 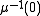 equals the pullback of
equals the pullback of 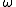 to
to 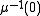 . Thus the quotient is a symplectic manifold, called the Marsden–Weinstein quotient, symplectic quotient or symplectic reduction of M by G and is denoted
. Thus the quotient is a symplectic manifold, called the Marsden–Weinstein quotient, symplectic quotient or symplectic reduction of M by G and is denoted 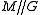 . Its dimension equals the dimension of M minus twice the dimension of G.
. Its dimension equals the dimension of M minus twice the dimension of G.

