
Symplectic cut
Encyclopedia
In mathematics
, specifically in symplectic geometry, the symplectic cut is a geometric modification on symplectic manifold
s. Its effect is to decompose a given manifold into two pieces. There is an inverse operation, the symplectic sum
, that glues two manifolds together into one. The symplectic cut can also be viewed as a generalization of symplectic blow up
. The cut was introduced in 1995 by Eugene Lerman, who used it to study the symplectic quotient
and other operations on manifolds.
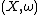 be any symplectic manifold and
be any symplectic manifold and
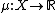
a Hamiltonian
on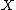 . Let
. Let  be any regular value of
be any regular value of 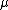 , so that the level set
, so that the level set 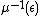 is a smooth manifold. Assume furthermore that
is a smooth manifold. Assume furthermore that 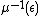 is fibered in circles, each of which is an integral curve of the induced Hamiltonian vector field
is fibered in circles, each of which is an integral curve of the induced Hamiltonian vector field
.
Under these assumptions,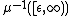 is a manifold with boundary
is a manifold with boundary 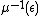 , and one can form a manifold
, and one can form a manifold
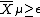
by collapsing each circle fiber to a point. In other words, is
is 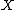 with the subset
with the subset 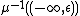 removed and the boundary collapsed along each circle fiber. The quotient of the boundary is a submanifold of
removed and the boundary collapsed along each circle fiber. The quotient of the boundary is a submanifold of 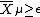 of codimension
of codimension
two, denoted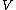 .
.
Similarly, one may form from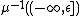 a manifold
a manifold  , which also contains a copy of
, which also contains a copy of 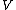 . The symplectic cut is the pair of manifolds
. The symplectic cut is the pair of manifolds 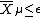 and
and  .
.
Sometimes it is useful to view the two halves of the symplectic cut as being joined along their shared submanifold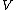 to produce a singular space
to produce a singular space
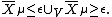
For example, this singular space is the central fiber in the symplectic sum regarded as a deformation.
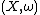 be any symplectic manifold. Assume that the circle group
be any symplectic manifold. Assume that the circle group 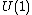 acts
acts
on in a Hamiltonian
in a Hamiltonian
way with moment map
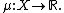
This moment map can be viewed as a Hamiltonian function that generates the circle action. The product space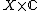 , with coordinate
, with coordinate  on
on 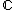 , comes with an induced symplectic form
, comes with an induced symplectic form
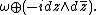
The group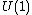 acts on the product in a Hamiltonian way by
acts on the product in a Hamiltonian way by

with moment map
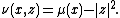
Let be any real number such that the circle action is free on
be any real number such that the circle action is free on 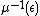 . Then
. Then  is a regular value of
is a regular value of  , and
, and 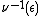 is a manifold.
is a manifold.
This manifold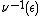 contains as a submanifold the set of points
contains as a submanifold the set of points 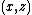 with
with 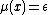 and
and 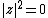 ; this submanifold is naturally identified with
; this submanifold is naturally identified with 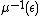 . The complement of the submanifold, which consists of points
. The complement of the submanifold, which consists of points 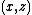 with
with 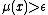 , is naturally identified with the product of
, is naturally identified with the product of
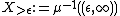
and the circle.
The manifold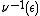 inherits the Hamiltonian circle action, as do its two submanifolds just described. So one may form the symplectic quotient
inherits the Hamiltonian circle action, as do its two submanifolds just described. So one may form the symplectic quotient
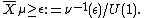
By construction, it contains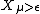 as a dense open submanifold; essentially, it compactifies this open manifold with the symplectic quotient
as a dense open submanifold; essentially, it compactifies this open manifold with the symplectic quotient
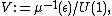
which is a symplectic submanifold of of codimension two.
of codimension two.
If is Kähler
is Kähler
, then so is the cut space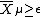 ; however, the embedding of
; however, the embedding of 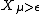 is not an isometry.
is not an isometry.
One constructs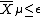 , the other half of the symplectic cut, in a symmetric manner. The normal bundle
, the other half of the symplectic cut, in a symmetric manner. The normal bundle
s of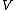 in the two halves of the cut are opposite each other (meaning symplectically anti-isomorphic). The symplectic sum of
in the two halves of the cut are opposite each other (meaning symplectically anti-isomorphic). The symplectic sum of  and
and 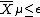 along
along  recovers
recovers 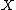 .
.
The existence of a global Hamiltonian circle action on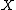 appears to be a restrictive assumption. However, it is not actually necessary; the cut can be performed under more general hypotheses, such as a local Hamiltonian circle action near
appears to be a restrictive assumption. However, it is not actually necessary; the cut can be performed under more general hypotheses, such as a local Hamiltonian circle action near 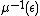 (since the cut is a local operation).
(since the cut is a local operation).
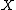 is blown up along a submanifold
is blown up along a submanifold 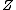 , the blow up locus
, the blow up locus
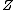 is replaced by an exceptional divisor
is replaced by an exceptional divisor
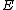 and the rest of the manifold is left undisturbed. Topologically, this operation may also be viewed as the removal of an
and the rest of the manifold is left undisturbed. Topologically, this operation may also be viewed as the removal of an  -neighborhood of the blow up locus, followed by the collapse of the boundary by the Hopf map.
-neighborhood of the blow up locus, followed by the collapse of the boundary by the Hopf map.
Blowing up a symplectic manifold is more subtle, since the symplectic form must be adjusted in a neighborhood of the blow up locus in order to continue smoothly across the exceptional divisor in the blow up. The symplectic cut is an elegant means of making the neighborhood-deletion/boundary-collapse process symplectically rigorous.
As before, let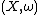 be a symplectic manifold with a Hamiltonian
be a symplectic manifold with a Hamiltonian 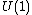 -action with moment map
-action with moment map 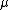 . Assume that the moment map is proper and that it achieves its maximum
. Assume that the moment map is proper and that it achieves its maximum 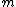 exactly along a symplectic submanifold
exactly along a symplectic submanifold 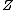 of
of 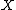 . Assume furthermore that the weights of the isotropy representation of
. Assume furthermore that the weights of the isotropy representation of 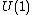 on the normal bundle
on the normal bundle 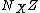 are all
are all 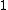 .
.
Then for small the only critical points in
the only critical points in 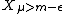 are those on
are those on 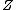 . The symplectic cut
. The symplectic cut 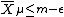 , which is formed by deleting a symplectic
, which is formed by deleting a symplectic  -neighborhood of
-neighborhood of 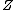 and collapsing the boundary, is then the symplectic blow up of
and collapsing the boundary, is then the symplectic blow up of 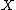 along
along  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in symplectic geometry, the symplectic cut is a geometric modification on symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s. Its effect is to decompose a given manifold into two pieces. There is an inverse operation, the symplectic sum
Symplectic sum
In mathematics, specifically in symplectic geometry, the symplectic sum is a geometric modification on symplectic manifolds, which glues two given manifolds into a single new one. It is a symplectic version of connected summation along a submanifold, often called a fiber sum.The symplectic sum is...
, that glues two manifolds together into one. The symplectic cut can also be viewed as a generalization of symplectic blow up
Blowing up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point...
. The cut was introduced in 1995 by Eugene Lerman, who used it to study the symplectic quotient
Moment map
In mathematics, specifically in symplectic geometry, the momentum map is a tool associated with a Hamiltonian action of a Lie group on a symplectic manifold, used to construct conserved quantities for the action. The moment map generalizes the classical notions of linear and angular momentum...
and other operations on manifolds.
Topological description
Let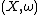 be any symplectic manifold and
be any symplectic manifold and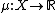
a Hamiltonian
Hamiltonian vector field
In mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
on
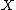 . Let
. Let  be any regular value of
be any regular value of 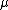 , so that the level set
, so that the level set 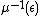 is a smooth manifold. Assume furthermore that
is a smooth manifold. Assume furthermore that 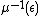 is fibered in circles, each of which is an integral curve of the induced Hamiltonian vector field
is fibered in circles, each of which is an integral curve of the induced Hamiltonian vector fieldHamiltonian vector field
In mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
.
Under these assumptions,
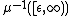 is a manifold with boundary
is a manifold with boundary 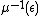 , and one can form a manifold
, and one can form a manifold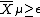
by collapsing each circle fiber to a point. In other words,
 is
is 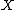 with the subset
with the subset 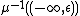 removed and the boundary collapsed along each circle fiber. The quotient of the boundary is a submanifold of
removed and the boundary collapsed along each circle fiber. The quotient of the boundary is a submanifold of 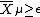 of codimension
of codimensionCodimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
two, denoted
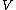 .
.Similarly, one may form from
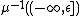 a manifold
a manifold  , which also contains a copy of
, which also contains a copy of 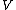 . The symplectic cut is the pair of manifolds
. The symplectic cut is the pair of manifolds 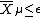 and
and  .
.Sometimes it is useful to view the two halves of the symplectic cut as being joined along their shared submanifold
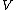 to produce a singular space
to produce a singular space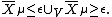
For example, this singular space is the central fiber in the symplectic sum regarded as a deformation.
Symplectic description
The preceding description is rather crude; more care is required to keep track of the symplectic structure on the symplectic cut. For this, let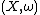 be any symplectic manifold. Assume that the circle group
be any symplectic manifold. Assume that the circle group 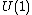 acts
actsGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on
 in a Hamiltonian
in a HamiltonianMoment map
In mathematics, specifically in symplectic geometry, the momentum map is a tool associated with a Hamiltonian action of a Lie group on a symplectic manifold, used to construct conserved quantities for the action. The moment map generalizes the classical notions of linear and angular momentum...
way with moment map
Moment map
In mathematics, specifically in symplectic geometry, the momentum map is a tool associated with a Hamiltonian action of a Lie group on a symplectic manifold, used to construct conserved quantities for the action. The moment map generalizes the classical notions of linear and angular momentum...
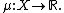
This moment map can be viewed as a Hamiltonian function that generates the circle action. The product space
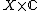 , with coordinate
, with coordinate  on
on 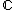 , comes with an induced symplectic form
, comes with an induced symplectic form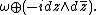
The group
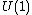 acts on the product in a Hamiltonian way by
acts on the product in a Hamiltonian way by
with moment map
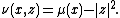
Let
 be any real number such that the circle action is free on
be any real number such that the circle action is free on 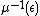 . Then
. Then  is a regular value of
is a regular value of  , and
, and 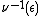 is a manifold.
is a manifold.This manifold
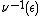 contains as a submanifold the set of points
contains as a submanifold the set of points 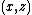 with
with 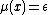 and
and 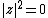 ; this submanifold is naturally identified with
; this submanifold is naturally identified with 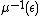 . The complement of the submanifold, which consists of points
. The complement of the submanifold, which consists of points 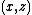 with
with 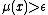 , is naturally identified with the product of
, is naturally identified with the product of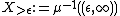
and the circle.
The manifold
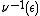 inherits the Hamiltonian circle action, as do its two submanifolds just described. So one may form the symplectic quotient
inherits the Hamiltonian circle action, as do its two submanifolds just described. So one may form the symplectic quotient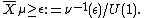
By construction, it contains
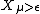 as a dense open submanifold; essentially, it compactifies this open manifold with the symplectic quotient
as a dense open submanifold; essentially, it compactifies this open manifold with the symplectic quotient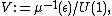
which is a symplectic submanifold of
 of codimension two.
of codimension two.If
 is Kähler
is KählerKähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
, then so is the cut space
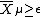 ; however, the embedding of
; however, the embedding of 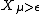 is not an isometry.
is not an isometry.One constructs
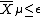 , the other half of the symplectic cut, in a symmetric manner. The normal bundle
, the other half of the symplectic cut, in a symmetric manner. The normal bundleNormal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
s of
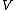 in the two halves of the cut are opposite each other (meaning symplectically anti-isomorphic). The symplectic sum of
in the two halves of the cut are opposite each other (meaning symplectically anti-isomorphic). The symplectic sum of  and
and 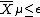 along
along  recovers
recovers 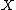 .
.The existence of a global Hamiltonian circle action on
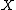 appears to be a restrictive assumption. However, it is not actually necessary; the cut can be performed under more general hypotheses, such as a local Hamiltonian circle action near
appears to be a restrictive assumption. However, it is not actually necessary; the cut can be performed under more general hypotheses, such as a local Hamiltonian circle action near 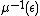 (since the cut is a local operation).
(since the cut is a local operation).Blow up as cut
When a complex manifoldComplex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
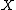 is blown up along a submanifold
is blown up along a submanifold 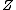 , the blow up locus
, the blow up locusLocus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
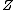 is replaced by an exceptional divisor
is replaced by an exceptional divisorExceptional divisor
In mathematics, specifically algebraic geometry, an exceptional divisor for a regular mapf: X \rightarrow Yof varieties is a kind of 'large' subvariety of X which is 'crushed' by f, in a certain definite sense...
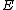 and the rest of the manifold is left undisturbed. Topologically, this operation may also be viewed as the removal of an
and the rest of the manifold is left undisturbed. Topologically, this operation may also be viewed as the removal of an  -neighborhood of the blow up locus, followed by the collapse of the boundary by the Hopf map.
-neighborhood of the blow up locus, followed by the collapse of the boundary by the Hopf map.Blowing up a symplectic manifold is more subtle, since the symplectic form must be adjusted in a neighborhood of the blow up locus in order to continue smoothly across the exceptional divisor in the blow up. The symplectic cut is an elegant means of making the neighborhood-deletion/boundary-collapse process symplectically rigorous.
As before, let
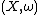 be a symplectic manifold with a Hamiltonian
be a symplectic manifold with a Hamiltonian 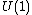 -action with moment map
-action with moment map 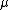 . Assume that the moment map is proper and that it achieves its maximum
. Assume that the moment map is proper and that it achieves its maximum 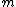 exactly along a symplectic submanifold
exactly along a symplectic submanifold 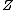 of
of 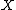 . Assume furthermore that the weights of the isotropy representation of
. Assume furthermore that the weights of the isotropy representation of 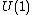 on the normal bundle
on the normal bundle 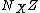 are all
are all 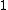 .
.Then for small
 the only critical points in
the only critical points in 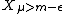 are those on
are those on 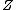 . The symplectic cut
. The symplectic cut 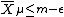 , which is formed by deleting a symplectic
, which is formed by deleting a symplectic  -neighborhood of
-neighborhood of 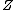 and collapsing the boundary, is then the symplectic blow up of
and collapsing the boundary, is then the symplectic blow up of 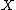 along
along  .
.

