Martin's axiom
Encyclopedia
In the mathematical field of set theory
, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis
, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH. Indeed, it is only really of interest when the continuum hypothesis fails (otherwise it adds nothing to ZFC). It can informally be considered to say that all cardinals less than the cardinality of the continuum
,
, behave roughly like 
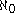. The intuition behind this can be understood by studying the proof of the Rasiowa-Sikorski lemma. More formally it is a principle that is used to control certain forcing
arguments.
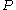satisfying the countable chain condition
(hereafter ccc) and any family
of dense sets in 
, whose cardinality 
is at most k, there is a filter
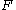on 
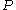such that 
∩ 
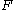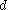is non-empty
for every
. MA, then, says that MA(k) holds for every k less than the continuum. (It is a theorem of ZFC that MA(
) fails.) Note that, in this case (for application of ccc), an antichain is a subset 
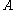of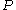 
such that any two distinct members of 
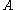are incompatible (two elements are said to be compatible if there exists a common element below both of them in the partial order). This differs from, for example, the notion of antichain in the context of trees
.
MA(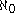
) is simply true. This is known as the Rasiowa-Sikorski lemma.
MA(
) is false: [0, 1] is a compact
Hausdorff space
, which is separable and so ccc. It has no isolated point
s, so points in it are nowhere dense, but it is the union of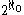
many points.
and topological consequences:
MA(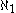
) is particularly interesting. Some consequences include:
MA together with the negation of the continuum hypothesis implies:
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH. Indeed, it is only really of interest when the continuum hypothesis fails (otherwise it adds nothing to ZFC). It can informally be considered to say that all cardinals less than the cardinality of the continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
,
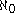, behave roughly like . The intuition behind this can be understood by studying the proof of the Rasiowa-Sikorski lemma. More formally it is a principle that is used to control certain forcingForcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
arguments.
Statement of Martin's axiom
The various statements of Martin's axiom typically take two parts. MA(k) says that for any partial order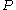 satisfying the countable chain conditionCountable chain condition
In order theory, a partially ordered set X is said to satisfy the countable chain condition, or to be ccc, if every strong antichain in X is countable. There are really two conditions: the upwards and downwards countable chain conditions. These are not equivalent...
(hereafter ccc) and any family
of dense sets in , whose cardinality is at most k, there is a filterFilter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
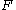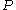on such that 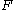∩ 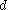is non-emptyEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
for every
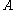. MA, then, says that MA(k) holds for every k less than the continuum. (It is a theorem of ZFC that MA() fails.) Note that, in this case (for application of ccc), an antichain is a subset of 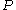such that any two distinct members of 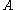are incompatible (two elements are said to be compatible if there exists a common element below both of them in the partial order). This differs from, for example, the notion of antichain in the context of treesTree (set theory)
In set theory, a tree is a partially ordered set In set theory, a tree is a partially ordered set (poset) In set theory, a tree is a partially ordered set (poset) (T, In set theory, a tree is a partially ordered set (poset) (T, ...
.
MA(
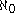) is simply true. This is known as the Rasiowa-Sikorski lemma.MA(
) is false: [0, 1] is a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, which is separable and so ccc. It has no isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s, so points in it are nowhere dense, but it is the union of
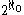many points.Equivalent forms of MA(k)
The following statements are equivalent to Martin's axiom:- If X is a compact Hausdorff topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
which satisfies the ccc then X is not the union of k or fewer nowhere dense subsets.
- If P is a non-empty upwards ccc poset and Y is a family of cofinal subsets of P with
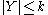then there is an upwards directed set A such that A meets every element of Y.
- Let A be a non-zero ccc Boolean algebra and F a family of subsets of A with
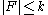. Then there is a boolean homomorphism 
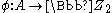such that for every 
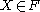either there is an 
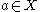with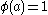 
or there is an upper bound b for X with 
.
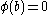Consequences of MA(k)
Martin's axiom has a number of other interesting combinatorial, analyticMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and topological consequences:
- The union of k or fewer null setNull setIn mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
s in an atomless
-finite Borel measure on a Polish spacePolish spaceIn the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
is null. In particular, the union of k or fewer subsets of
of Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
0 also has Lebesgue measure 0.
- A compact Hausdorff space X with
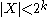is sequentially compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, i.e., every sequence has a convergent subsequence.
- No non-principal ultrafilterUltrafilterIn the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
on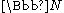
has a base of cardinality < k.
- Equivalently for any
: 
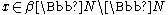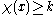, where 
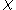is the character of x, and so 
.
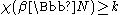MA(
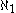) is particularly interesting. Some consequences include:- A product of ccc topological spaces is ccc (this in turn implies there are no Suslin lines).
MA together with the negation of the continuum hypothesis implies:
- There exists a Whitehead groupWhitehead groupWhitehead group in mathematics may mean:* A group W with Ext=0; see Whitehead problem* For a ring, the Whitehead group Wh of a ring A, equal to K_1...
that is not free; ShelahSaharon ShelahSaharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
used this to show that the Whitehead problemWhitehead problemIn group theory, a branch of abstract algebra, the Whitehead problem is the following question:Shelah proved that Whitehead's problem is undecidable within standard ZFC set theory.-Refinement:...
is independent of ZFC.
See also
- Martin's axiom has generalizations called the proper forcing axiomProper Forcing AxiomIn the mathematical field of set theory, the proper forcing axiom is a significant strengthening of Martin's axiom, where forcings with the countable chain condition are replaced by proper forcings.- Statement :...
and Martin's maximumMartin's maximumIn set theory, Martin's maximum, introduced by , is a generalization of the proper forcing axiom, which is in turn a generalization of Martin's axiom....
. - Sheldon W.Davis has suggested that Martin's axiom is motivated by Baire category theoremBaire category theoremThe Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
in his book.