
Magnus expansion
Encyclopedia
In mathematics
and physics
, the Magnus expansion, named after Wilhelm Magnus
(1907–1990), provides an exponential representation of the solution of a first order linear homogeneous differential equation
for a linear operator. In particular it furnishes the fundamental matrix of a system of linear ordinary differential equations of order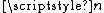 with varying coefficients. The exponent is built up as an infinite series whose terms involve multiple integrals and nested commutators.
with varying coefficients. The exponent is built up as an infinite series whose terms involve multiple integrals and nested commutators.
associated with the linear ordinary differential equation
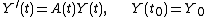
for the unknown n-dimensional vector function Y(t).
When n = 1, the solution reads
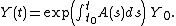
This is still valid for n > 1 if the matrix A(t) satisfies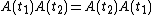 for any pair of values of t, t1 and t2. In particular, this is the case if the matrix
for any pair of values of t, t1 and t2. In particular, this is the case if the matrix 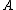 is constant. In the general case, however, the expression above is no longer the solution of the problem.
is constant. In the general case, however, the expression above is no longer the solution of the problem.
The approach proposed by Magnus to solve the matrix initial value problem is to express the solution by means of the exponential of a certain n × n matrix function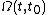 ,
,
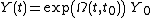
which is subsequently constructed as a series
expansion,
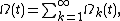
where, for the sake of simplicity, it is customary to write down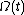 for
for 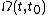 and to take t0 = 0. The equation above constitutes the Magnus expansion or Magnus series for the solution of matrix linear initial value problem.
and to take t0 = 0. The equation above constitutes the Magnus expansion or Magnus series for the solution of matrix linear initial value problem.
The first four terms of this series read
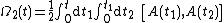

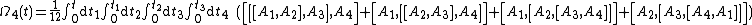
where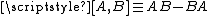 is the matrix commutator
is the matrix commutator
of A and B.
These equations may be interpreted as follows: coincides exactly with the exponent in the scalar (n = 1) case, but this equation cannot give the whole solution. If one insists in having an exponential representation the exponent has to be corrected. The rest of the Magnus series provides that correction.
coincides exactly with the exponent in the scalar (n = 1) case, but this equation cannot give the whole solution. If one insists in having an exponential representation the exponent has to be corrected. The rest of the Magnus series provides that correction.
In applications one can rarely sum exactly the Magnus series and has to truncate it to get approximate solutions. The main advantage of the Magnus proposal is that, very often, the truncated series still shares with the exact solution important qualitative properties, at variance with other conventional perturbation
theories. For instance, in classical mechanics
the symplectic character of the time evolution
is preserved at every order of approximation. Similarly the unitary
character of the time evolution operator in quantum mechanics
is also preserved (in contrast to the Dyson series
).
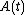 , when can the exponent
, when can the exponent 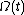 be obtained as the sum of the Magnus series? A sufficient condition for this series to converge for
be obtained as the sum of the Magnus series? A sufficient condition for this series to converge for 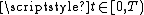 is
is
where denotes a matrix norm. This result is generic, in the sense that one may consider specific matrices
denotes a matrix norm. This result is generic, in the sense that one may consider specific matrices 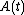 for which the series diverges for any
for which the series diverges for any 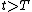 .
.
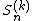 defined recursively through
defined recursively through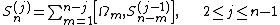
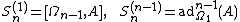
one has
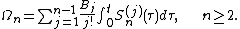
Here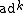 is a shorthand for an iterated commutator,
is a shorthand for an iterated commutator,
and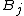 are the Bernoulli numbers.
are the Bernoulli numbers.
When this recursion is worked out explicitly, it is possible to express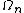 as a linear combination of
as a linear combination of  -fold integrals of
-fold integrals of  nested commutators containing
nested commutators containing  matrices
matrices 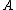 ,
,
an expression that becomes increasingly intricate with .
.
and molecular physics
to nuclear magnetic resonance
and quantum electrodynamics
. It has been also used since 1998 as a tool to construct practical algorithms for the numerical integration of matrix linear differential equations. As they inherit from the Magnus expansion the
preservation of qualitative traits of the problem, the corresponding schemes are prototypical examples of geometric numerical integrators
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Magnus expansion, named after Wilhelm Magnus
Wilhelm Magnus
Wilhelm Magnus was a mathematician. He made important contributions in combinatorial group theory, Lie algebras, mathematical physics, elliptic functions, and the study of tessellations....
(1907–1990), provides an exponential representation of the solution of a first order linear homogeneous differential equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
for a linear operator. In particular it furnishes the fundamental matrix of a system of linear ordinary differential equations of order
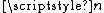 with varying coefficients. The exponent is built up as an infinite series whose terms involve multiple integrals and nested commutators.
with varying coefficients. The exponent is built up as an infinite series whose terms involve multiple integrals and nested commutators.Magnus approach and its interpretation
Given the n × n coefficient matrix A(t) we want to solve the initial value problemInitial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
associated with the linear ordinary differential equation
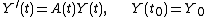
for the unknown n-dimensional vector function Y(t).
When n = 1, the solution reads
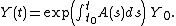
This is still valid for n > 1 if the matrix A(t) satisfies
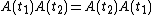 for any pair of values of t, t1 and t2. In particular, this is the case if the matrix
for any pair of values of t, t1 and t2. In particular, this is the case if the matrix 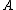 is constant. In the general case, however, the expression above is no longer the solution of the problem.
is constant. In the general case, however, the expression above is no longer the solution of the problem.The approach proposed by Magnus to solve the matrix initial value problem is to express the solution by means of the exponential of a certain n × n matrix function
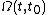 ,
,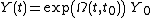
which is subsequently constructed as a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
expansion,
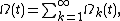
where, for the sake of simplicity, it is customary to write down
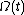 for
for 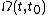 and to take t0 = 0. The equation above constitutes the Magnus expansion or Magnus series for the solution of matrix linear initial value problem.
and to take t0 = 0. The equation above constitutes the Magnus expansion or Magnus series for the solution of matrix linear initial value problem.The first four terms of this series read

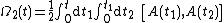

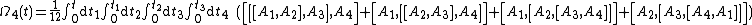
where
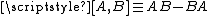 is the matrix commutator
is the matrix commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
of A and B.
These equations may be interpreted as follows:
 coincides exactly with the exponent in the scalar (n = 1) case, but this equation cannot give the whole solution. If one insists in having an exponential representation the exponent has to be corrected. The rest of the Magnus series provides that correction.
coincides exactly with the exponent in the scalar (n = 1) case, but this equation cannot give the whole solution. If one insists in having an exponential representation the exponent has to be corrected. The rest of the Magnus series provides that correction.In applications one can rarely sum exactly the Magnus series and has to truncate it to get approximate solutions. The main advantage of the Magnus proposal is that, very often, the truncated series still shares with the exact solution important qualitative properties, at variance with other conventional perturbation
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
theories. For instance, in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
the symplectic character of the time evolution
Time evolution
Time evolution is the change of state brought about by the passage of time, applicable to systems with internal state . In this formulation, time is not required to be a continuous parameter, but may be discrete or even finite. In classical physics, time evolution of a collection of rigid bodies...
is preserved at every order of approximation. Similarly the unitary
Unitary
Unitary may refer to:* Unitary construction, in automotive design, another common term for a unibody or monocoque construction**Unitary as chemical weapons opposite of Binary...
character of the time evolution operator in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
is also preserved (in contrast to the Dyson series
Dyson series
In scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
).
Convergence of the expansion
From a mathematical point of view, the convergence problem is the following: given a certain matrix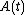 , when can the exponent
, when can the exponent 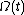 be obtained as the sum of the Magnus series? A sufficient condition for this series to converge for
be obtained as the sum of the Magnus series? A sufficient condition for this series to converge for 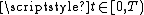 is
is
where
 denotes a matrix norm. This result is generic, in the sense that one may consider specific matrices
denotes a matrix norm. This result is generic, in the sense that one may consider specific matrices 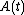 for which the series diverges for any
for which the series diverges for any 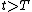 .
.Magnus generator
It is possible to design a recursive procedure to generate all the terms in the Magnus expansion. Specifically, with the matrices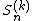 defined recursively through
defined recursively through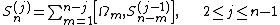
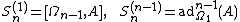
one has

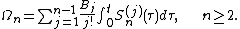
Here
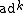 is a shorthand for an iterated commutator,
is a shorthand for an iterated commutator,
and
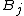 are the Bernoulli numbers.
are the Bernoulli numbers.When this recursion is worked out explicitly, it is possible to express
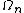 as a linear combination of
as a linear combination of  -fold integrals of
-fold integrals of  nested commutators containing
nested commutators containing  matrices
matrices 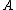 ,
,
an expression that becomes increasingly intricate with
 .
.Applications
Since the 1960s, the Magnus expansion has been successfully applied as a perturbative tool in numerous areas of physics and chemistry, from atomicAtomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
and molecular physics
Molecular physics
Molecular physics is the study of the physical properties of molecules, the chemical bonds between atoms as well as the molecular dynamics. Its most important experimental techniques are the various types of spectroscopy...
to nuclear magnetic resonance
Nuclear magnetic resonance
Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...
and quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
. It has been also used since 1998 as a tool to construct practical algorithms for the numerical integration of matrix linear differential equations. As they inherit from the Magnus expansion the
preservation of qualitative traits of the problem, the corresponding schemes are prototypical examples of geometric numerical integrators
Geometric integrator
In the mathematical field of numerical ordinary differential equations, a geometric integrator is a numerical method that preserves geometric properties of the exact flow of a differential equation.-Pendulum example:...
.

