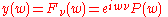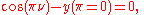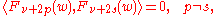Floquet theory
Encyclopedia
Floquet theory is a branch of the theory of ordinary differential equations relating to the class of solutions to linear differential equation
s of the form
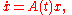
with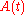 a piecewise continuous periodic function with period
a piecewise continuous periodic function with period  .
.
The main theorem of Floquet theory, Floquet's theorem, due to , gives a canonical form
for each fundamental matrix solution
of this common linear system
. It gives a coordinate change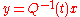 with
with  that transforms the periodic system to a traditional linear system with constant, real coefficients.
that transforms the periodic system to a traditional linear system with constant, real coefficients.
In solid-state physics
, the analogous result (generalized to three dimensions) is known as Bloch's theorem
.
Note that the solutions of the linear differential equation form a vector space. A matrix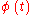 is called a fundamental matrix solution if all columns are linearly independent solutions. A matrix
is called a fundamental matrix solution if all columns are linearly independent solutions. A matrix  is called a principal fundamental matrix solution if all columns are linearly independent solutions and there exists
is called a principal fundamental matrix solution if all columns are linearly independent solutions and there exists 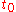 such that
such that 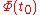 is the identity. A principal fundamental matrix can be constructed from a fundamental matrix using
is the identity. A principal fundamental matrix can be constructed from a fundamental matrix using  . The solution of the linear differential equation with the initial condition
. The solution of the linear differential equation with the initial condition  is
is 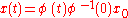 where
where 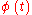 is any fundamental matrix solution.
is any fundamental matrix solution.
Let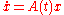 be a linear first order differential equation,
be a linear first order differential equation,
where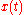 is a column vector of length
is a column vector of length  and
and 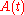 an
an 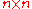 periodic matrix with period
periodic matrix with period  (that is
(that is 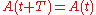 for all real values of
for all real values of  ). Let
). Let 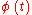 be a fundamental matrix solution of this differential equation. Then, for all
be a fundamental matrix solution of this differential equation. Then, for all 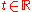 ,
,
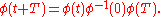
In addition, for each matrix (possibly complex) such that
(possibly complex) such that
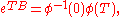
there is a periodic (period ) matrix function
) matrix function 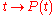 such that
such that

Also, there is a real matrix and a real periodic (period-
and a real periodic (period- ) matrix function
) matrix function 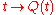 such that
such that

In the above ,
, 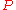 ,
,  and
and  are
are 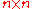 matrices.
matrices.
 gives rise to a time-dependent change of coordinates (
gives rise to a time-dependent change of coordinates ( ), under which our original system becomes a linear system with real constant coefficients
), under which our original system becomes a linear system with real constant coefficients  . Since
. Since 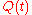 is continuous and periodic it must be bounded. Thus the stability of the zero solution for
is continuous and periodic it must be bounded. Thus the stability of the zero solution for 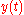 and
and 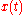 is determined by the eigenvalues of
is determined by the eigenvalues of  .
.
The representation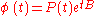 is called a Floquet normal form for the fundamental matrix
is called a Floquet normal form for the fundamental matrix 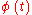 .
.
The eigenvalues of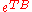 are called the characteristic multiplier
are called the characteristic multiplier
s of the system. They are also the eigenvalues of the (linear) Poincaré maps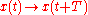 . A Floquet exponent (sometimes called a characteristic exponent), is a complex
. A Floquet exponent (sometimes called a characteristic exponent), is a complex  such that
such that 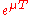 is a characteristic multiplier of the system. Notice that Floquet exponents are not unique, since
is a characteristic multiplier of the system. Notice that Floquet exponents are not unique, since 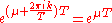 , where
, where 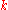 is an integer. The real parts of the Floquet exponents are called Lyapunov exponents. The zero solution is asymptotically stable if all Lyapunov exponents are negative, Lyapunov stable
is an integer. The real parts of the Floquet exponents are called Lyapunov exponents. The zero solution is asymptotically stable if all Lyapunov exponents are negative, Lyapunov stable
if the Lyapunov exponents are nonpositive and unstable otherwise.
Given , the Mathieu equation is given by
, the Mathieu equation is given by
The Mathieu equation is a linear second-order differential equation with periodic coefficients.
One of the most powerful results of Mathieu's functions is the Floquet's Theorem [1, 2].
It states that periodic solutions of Mathieu equation for any pair (a, q) can be expressed in the form
or
where is a constant depending on a and q and P(.) is
is a constant depending on a and q and P(.) is  -periodic in w.
-periodic in w.
The constant is called the characteristic exponent.
is called the characteristic exponent.
If is an integer, then
is an integer, then 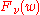 and
and 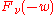 are linear dependent solutions. Furthermore,
are linear dependent solutions. Furthermore,
for the solution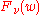 or
or 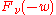 , respectively.
, respectively.
We assume that the pair (a, q) is such that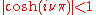 so that the solution
so that the solution 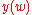 is bounded on the real axis. General solution of Mathieu's equation (
is bounded on the real axis. General solution of Mathieu's equation ( ,
,  non-integer) is the form
non-integer) is the form
where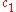 and
and 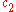 are arbitrary constants.
are arbitrary constants.
All bounded solutions --those of fractional as well as integral order-- are described by an infinite series of harmonic oscillations whose amplitudes decrease with increasing frequency.
Another very important property of Mathieu's functions is the orthogonality [3]:
If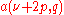 and
and 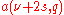 are simple roots of
are simple roots of
then:
i.e.,
where <.,.> denotes an inner product defined from 0 to π.
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
s of the form
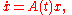
with
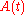 a piecewise continuous periodic function with period
a piecewise continuous periodic function with period  .
.The main theorem of Floquet theory, Floquet's theorem, due to , gives a canonical form
Canonical form
Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
for each fundamental matrix solution
Fundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
of this common linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
. It gives a coordinate change
 with
with  that transforms the periodic system to a traditional linear system with constant, real coefficients.
that transforms the periodic system to a traditional linear system with constant, real coefficients.In solid-state physics
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
, the analogous result (generalized to three dimensions) is known as Bloch's theorem
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
.
Note that the solutions of the linear differential equation form a vector space. A matrix
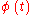 is called a fundamental matrix solution if all columns are linearly independent solutions. A matrix
is called a fundamental matrix solution if all columns are linearly independent solutions. A matrix  is called a principal fundamental matrix solution if all columns are linearly independent solutions and there exists
is called a principal fundamental matrix solution if all columns are linearly independent solutions and there exists 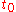 such that
such that 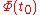 is the identity. A principal fundamental matrix can be constructed from a fundamental matrix using
is the identity. A principal fundamental matrix can be constructed from a fundamental matrix using  . The solution of the linear differential equation with the initial condition
. The solution of the linear differential equation with the initial condition  is
is 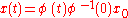 where
where 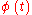 is any fundamental matrix solution.
is any fundamental matrix solution.Floquet's theorem
Let
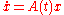 be a linear first order differential equation,
be a linear first order differential equation,where
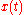 is a column vector of length
is a column vector of length  and
and 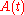 an
an 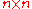 periodic matrix with period
periodic matrix with period  (that is
(that is 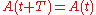 for all real values of
for all real values of  ). Let
). Let 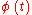 be a fundamental matrix solution of this differential equation. Then, for all
be a fundamental matrix solution of this differential equation. Then, for all 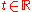 ,
,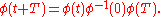
In addition, for each matrix
 (possibly complex) such that
(possibly complex) such that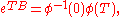
there is a periodic (period
 ) matrix function
) matrix function 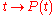 such that
such that
Also, there is a real matrix
 and a real periodic (period-
and a real periodic (period- ) matrix function
) matrix function 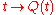 such that
such that
In the above
 ,
, 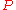 ,
,  and
and  are
are 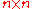 matrices.
matrices.Consequences and applications
This mapping gives rise to a time-dependent change of coordinates (
gives rise to a time-dependent change of coordinates ( ), under which our original system becomes a linear system with real constant coefficients
), under which our original system becomes a linear system with real constant coefficients  . Since
. Since 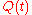 is continuous and periodic it must be bounded. Thus the stability of the zero solution for
is continuous and periodic it must be bounded. Thus the stability of the zero solution for 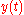 and
and 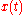 is determined by the eigenvalues of
is determined by the eigenvalues of  .
.The representation
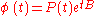 is called a Floquet normal form for the fundamental matrix
is called a Floquet normal form for the fundamental matrix 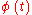 .
.The eigenvalues of
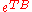 are called the characteristic multiplier
are called the characteristic multiplierCharacteristic multiplier
In mathematics, and particularly ordinary differential equations, a characteristic multiplier is an eigenvalue of a monodromy matrix. The logarithm of a characteristic multiplier is also known as characteristic exponent...
s of the system. They are also the eigenvalues of the (linear) Poincaré maps
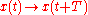 . A Floquet exponent (sometimes called a characteristic exponent), is a complex
. A Floquet exponent (sometimes called a characteristic exponent), is a complex  such that
such that 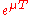 is a characteristic multiplier of the system. Notice that Floquet exponents are not unique, since
is a characteristic multiplier of the system. Notice that Floquet exponents are not unique, since 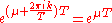 , where
, where 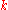 is an integer. The real parts of the Floquet exponents are called Lyapunov exponents. The zero solution is asymptotically stable if all Lyapunov exponents are negative, Lyapunov stable
is an integer. The real parts of the Floquet exponents are called Lyapunov exponents. The zero solution is asymptotically stable if all Lyapunov exponents are negative, Lyapunov stableLyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
if the Lyapunov exponents are nonpositive and unstable otherwise.
- Floquet theory is very important for the study of dynamical systems.
- Floquet theory shows stability in Hill differential equation (introduced by George William HillGeorge William HillGeorge William Hill , was an American astronomer and mathematician.Hill was born in New York City, New York to painter and engraver John William Hill. and Catherine Smith Hill. He moved to West Nyack with his family when he was eight years old. After attending high school, Hill graduated from...
) approximating the motion of the moonMoonThe Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
as a harmonic oscillatorHarmonic oscillatorIn classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
in a periodic gravitational fieldGravitational fieldThe gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
.
Floquet's theorem applied to Mathieu equation
Mathieu's equation is related to the wave equation for the elliptic cylinder.Given
 , the Mathieu equation is given by
, the Mathieu equation is given byThe Mathieu equation is a linear second-order differential equation with periodic coefficients.
One of the most powerful results of Mathieu's functions is the Floquet's Theorem [1, 2].
It states that periodic solutions of Mathieu equation for any pair (a, q) can be expressed in the form
or
where
 is a constant depending on a and q and P(.) is
is a constant depending on a and q and P(.) is  -periodic in w.
-periodic in w.The constant
 is called the characteristic exponent.
is called the characteristic exponent.If
 is an integer, then
is an integer, then 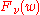 and
and 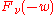 are linear dependent solutions. Furthermore,
are linear dependent solutions. Furthermore,for the solution
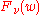 or
or 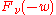 , respectively.
, respectively.We assume that the pair (a, q) is such that
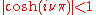 so that the solution
so that the solution 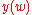 is bounded on the real axis. General solution of Mathieu's equation (
is bounded on the real axis. General solution of Mathieu's equation ( ,
,  non-integer) is the form
non-integer) is the formwhere
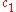 and
and 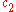 are arbitrary constants.
are arbitrary constants.All bounded solutions --those of fractional as well as integral order-- are described by an infinite series of harmonic oscillations whose amplitudes decrease with increasing frequency.
Another very important property of Mathieu's functions is the orthogonality [3]:
If
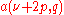 and
and 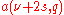 are simple roots of
are simple roots ofthen:
i.e.,
where <.,.> denotes an inner product defined from 0 to π.