
Oseledec theorem
Encyclopedia
In mathematics
, the multiplicative ergodic theorem, or Oseledets theorem provides the theoretical background for computation of Lyapunov exponent
s of a nonlinear dynamical system
. It was proved by Valery Oseledets (also spelled "Oseledec") in 1965 and reported at the International Mathematical Congress in Moscow in 1966. A conceptually different proof of the multiplicative ergodic theorem was found by M. S. Raghunathan. The theorem has been extended to semisimple Lie groups by V. A. Kaimanovich and further generalized in the works of David Ruelle
, Gregory Margulis, Anders Karlsson, and F. Ledrappier.
A cocycle of an autonomous dynamical system is a map
C : X×T → Rn×n satisfying
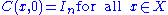
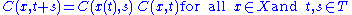
where X and T (with T = Z or T = R) are the phase space
and the time range, respectively, of the dynamical system,
and In is the n-dimensional unit matrix.
The dimension n of the matrices C is not related to the phase space X.
of the dynamical system such that ||C(x,t)|| and ||C(x,t)−1|| are L1-integrable
(i.e. such that C(x, t)−1 exists if T = Z). Then for μ-almost all x and each non-zero vector u∈Rn the limit
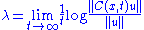
exists and assumes, depending on u but not on x, up to n different values,
these are the Lyapunov exponents.
Further, if λ1 > ... > λm
are the different limits then there are subspaces Rn = R1 ⊃ ... ⊃ Rm ⊃ Rm+1 = {0} such that the limit is λi for u∈ Ri\Ri+1 and i = 1, ..., m.
The values of the Lyapunov exponents are invariant with respect to a wide range of coordinate transformations. Suppose that g : X → X is a one-to-one map such that and its inverse exist then the values of the Lyapunov exponents do not change.
and its inverse exist then the values of the Lyapunov exponents do not change.
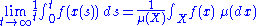
where the integrals and the limit exist.
Space average (right hand side, μ is an ergodic measure on X)
is the accumulation of f(x) values weighted by μ(dx).
Since addition is commutative, the accumulation of the f(x)μ(dx) values may be done in arbitrary order.
In contrast, the time average (left hand side) suggests a specific ordering
of the f(x(s)) values along the trajectory.
Since matrix multiplication is, in general, not commutative,
accumulation of multiplied cocycle values (and limits thereof) according to
C(x(t0),tk) = C(x(tk−1),tk − tk−1) ... C(x(t0),t1 − t0)
— for tk large and
the steps ti − ti−1 small — makes sense only for a prescribed ordering. Thus, the time average may exist (and the theorem states that it actually exists), but there is no space average counterpart. In other words, the Oseledets theorem differs from additive ergodic theorems (such as G. D. Birkhoff's and J. von Neumann's) in that it guarantees the existence of the time average, but makes no claim about the space average.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the multiplicative ergodic theorem, or Oseledets theorem provides the theoretical background for computation of Lyapunov exponent
Lyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
s of a nonlinear dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
. It was proved by Valery Oseledets (also spelled "Oseledec") in 1965 and reported at the International Mathematical Congress in Moscow in 1966. A conceptually different proof of the multiplicative ergodic theorem was found by M. S. Raghunathan. The theorem has been extended to semisimple Lie groups by V. A. Kaimanovich and further generalized in the works of David Ruelle
David Ruelle
David Pierre Ruelle is a Belgian-French mathematical physicist. He has worked on statistical physics and dynamical systems. With Floris Takens he coined the term strange attractor, and founded a new theory of turbulence...
, Gregory Margulis, Anders Karlsson, and F. Ledrappier.
Cocycles
The multiplicative ergodic theorem is stated in terms of matrix cocycles of a dynamical system. The theorem states conditions for the existence of the defining limits and describes the Lyapunov exponents. It does not address the rate of convergence.A cocycle of an autonomous dynamical system is a map
C : X×T → Rn×n satisfying
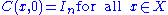
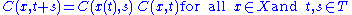
where X and T (with T = Z or T = R) are the phase space
and the time range, respectively, of the dynamical system,
and In is the n-dimensional unit matrix.
The dimension n of the matrices C is not related to the phase space X.
Examples
- A prominent example of a cocycle is given by the Matrix Jt in the theory of Lyapunov exponents. In this special case, the dimension n of the matrices is the same as the dimension of the manifold X.
- For any cocycle C, the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
det C(x, t) is a one-dimensional cocycle.
Statement of the theorem
Let μ be an invariant measure on X and C a cocycleof the dynamical system such that ||C(x,t)|| and ||C(x,t)−1|| are L1-integrable
(i.e. such that C(x, t)−1 exists if T = Z). Then for μ-almost all x and each non-zero vector u∈Rn the limit
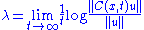
exists and assumes, depending on u but not on x, up to n different values,
these are the Lyapunov exponents.
Further, if λ1 > ... > λm
are the different limits then there are subspaces Rn = R1 ⊃ ... ⊃ Rm ⊃ Rm+1 = {0} such that the limit is λi for u∈ Ri\Ri+1 and i = 1, ..., m.
The values of the Lyapunov exponents are invariant with respect to a wide range of coordinate transformations. Suppose that g : X → X is a one-to-one map such that
 and its inverse exist then the values of the Lyapunov exponents do not change.
and its inverse exist then the values of the Lyapunov exponents do not change.Additive versus multiplicative ergodic theorems
Verbally, ergodicity means that time and space averages are equal, formally: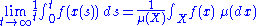
where the integrals and the limit exist.
Space average (right hand side, μ is an ergodic measure on X)
is the accumulation of f(x) values weighted by μ(dx).
Since addition is commutative, the accumulation of the f(x)μ(dx) values may be done in arbitrary order.
In contrast, the time average (left hand side) suggests a specific ordering
of the f(x(s)) values along the trajectory.
Since matrix multiplication is, in general, not commutative,
accumulation of multiplied cocycle values (and limits thereof) according to
C(x(t0),tk) = C(x(tk−1),tk − tk−1) ... C(x(t0),t1 − t0)
— for tk large and
the steps ti − ti−1 small — makes sense only for a prescribed ordering. Thus, the time average may exist (and the theorem states that it actually exists), but there is no space average counterpart. In other words, the Oseledets theorem differs from additive ergodic theorems (such as G. D. Birkhoff's and J. von Neumann's) in that it guarantees the existence of the time average, but makes no claim about the space average.

