A linear feedback shift register (LFSR) is a shift register

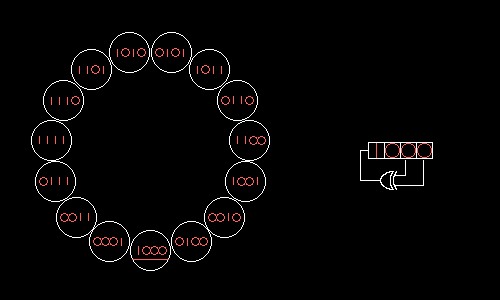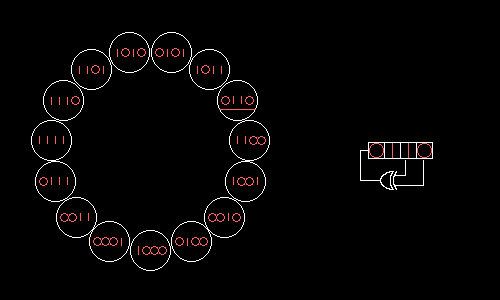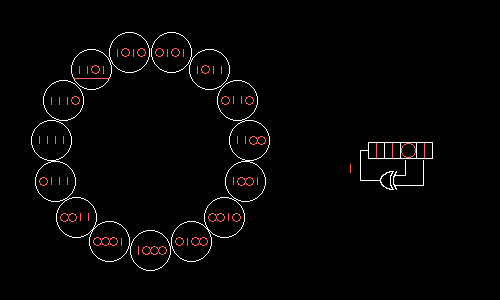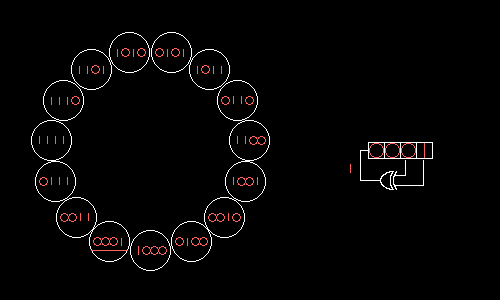
Shift register

In digital circuits, a shift register is a cascade of flip flops, sharing the same clock, which has the output of any one but the last flip-flop connected to the "data" input of the next one in the chain, resulting in a circuit that shifts by one position the one-dimensional "bit array" stored in...

 whose input bit is a linear function of its previous state.

The most commonly used linear function of single bits is XOR. Thus, an LFSR is most often a shift register whose input bit is driven by the exclusive-or (XOR) of some bits of the overall shift register value.

The initial value of the LFSR is called the seed, and because the operation of the register is deterministic, the stream of values produced by the register is completely determined by its current (or previous) state. Likewise, because the register has a finite number of possible states, it must eventually enter a repeating cycle. However, an LFSR with a well-chosen feedback function can produce a sequence of bits which appears random and which has a very long cycle.

Applications of LFSRs include generating pseudo-random numbers

Pseudorandomness

A pseudorandom process is a process that appears to be random but is not. Pseudorandom sequences typically exhibit statistical randomness while being generated by an entirely deterministic causal process...

, pseudo-noise sequences

Pseudorandom noise

In cryptography, pseudorandom noise is a signal similar to noise which satisfies one or more of the standard tests for statistical randomness....

, fast digital counters, and whitening sequences

Scrambler

In telecommunications, a scrambler is a device that transposes or inverts signals or otherwise encodes a message at the transmitter to make the message unintelligible at a receiver not equipped with an appropriately set descrambling device...

. Both hardware and software implementations of LFSRs are common.

The mathematics of a cyclic redundancy check

Cyclic redundancy check

A cyclic redundancy check is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to raw data...

, used to provide a quick check against transmission errors, are closely related to those of an LFSR.

Fibonacci LFSRs

The bit positions that affect the next state are called the taps. In the diagram the taps are [16,14,13,11]. The rightmost bit of the LFSR is called the output bit. The taps are XOR'd sequentially with the output bit and then fed back into the leftmost bit. The sequence of bits in the rightmost position is called the output stream.

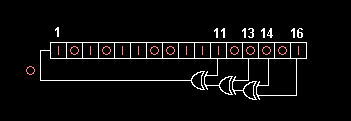
• The bits in the LFSR state which influence the input are called taps (white in the diagram).
• A maximum-length LFSR produces an m-sequence
  Maximum length sequence
  A maximum length sequence is a type of pseudorandom binary sequence.They are bit sequences generated using maximal linear feedback shift registers and are so called because they are periodic and reproduce every binary sequence that can be reproduced by the shift registers...
  
   (i.e. it cycles through all possible 2ⁿ − 1 states within the shift register except the state where all bits are zero), unless it contains all zeros, in which case it will never change.
• As an alternative to the XOR based feedback in an LFSR, one can also use XNOR. This function is an affine map
  Affine transformation
  In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
  
  , not strictly a linear map, but it results in an equivalent polynomial counter whose state of this counter is the complement of the state of an LFSR. A state with all ones is illegal when using an XNOR feedback, in the same way as a state with all zeroes is illegal when using XOR. This state is considered illegal because the counter would remain "locked-up" in this state.

The sequence of numbers generated by an LFSR or its XNOR counterpart can be considered a binary numeral system

Binary numeral system

The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...

 just as valid as Gray code

Gray code

The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only one bit. It is a non-weighted code....

 or the natural binary code.
The arrangement of taps for feedback in an LFSR can be expressed in finite field arithmetic

Finite field arithmetic

Arithmetic in a finite field is different from standard integer arithmetic. There are a limited number of elements in the finite field; all operations performed in the finite field result in an element within that field....

 as a polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

 mod

Modular arithmetic

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....

 2. This means that the coefficients of the polynomial must be 1's or 0's. This is called the feedback polynomial or characteristic polynomial. For example, if the taps are at the 16th, 14th, 13th and 11th bits (as shown), the feedback polynomial is


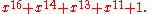
The 'one' in the polynomial does not correspond to a tap — it corresponds to the input to the first bit (i.e. x⁰, which is equivalent to 1). The powers of the terms represent the tapped bits, counting from the left. The first and last bits are always connected as an input and output tap respectively.

Tables of primitive polynomial

Primitive polynomial

In field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite extension field GF...

s from which maximum-length LFSRs can be constructed are given below and in the references.

• The LFSR will only be maximum-length if the number of taps is even
  Even and odd numbers
  In mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
  
  ; just 2 or 4 taps can suffice even for extremely long sequences.
• The set of taps — taken all together, not pairwise (i.e. as pairs of elements) — must be relatively prime. In other words, there must be no common divisor to all taps.
• There can be more than one maximum-length tap sequence for a given LFSR length
• Once one maximum-length tap sequence has been found, another automatically follows. If the tap sequence, in an n-bit LFSR, is [n, A, B, C, 0], where the 0 corresponds to the x⁰ = 1 term, then the corresponding 'mirror' sequence is [n, n − C, n − B, n − A, 0]. So the tap sequence [32, 7, 3, 2, 0] has as its counterpart [32, 30, 29, 25, 0]. Both give a maximum-length sequence.

Some example C code is below:

1. include

uint16_t lfsr = 0xACE1u;
unsigned bit;
unsigned period = 0;
do {
/* taps: 16 14 13 11; characteristic polynomial: x^16 + x^14 + x^13 + x^11 + 1 */
bit = ((lfsr >> 0) ^ (lfsr >> 2) ^ (lfsr >> 3) ^ (lfsr >> 5) ) & 1;
lfsr = (lfsr >> 1) | (bit << 15);
++period;
} while(lfsr != 0xACE1u);


The above code assumes the most significant bit of lfsr is bit 1, and the least significant bit is bit 16.

As well as Fibonacci, this LFSR configuration is also known as standard, many-to-one or external XOR gates. LFSR has an alternative configuration.

Galois LFSRs

Named after the French mathematician Évariste Galois

Évariste Galois

Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...

, an LFSR in Galois configuration, which is also known as modular, internal XORs as well as one-to-many LFSR, is an alternate structure that can generate the same output stream as a conventional LFSR. In the Galois configuration, when the system is clocked, bits that are not taps are shifted one position to the right unchanged. The taps, on the other hand, are XOR'd with the output bit before they are stored in the next position. The new output bit is the next input bit. The effect of this is that when the output bit is zero all the bits in the register shift to the right unchanged, and the input bit becomes zero. When the output bit is one, the bits in the tap positions all flip (if they are 0, they become 1, and if they are 1, they become 0), and then the entire register is shifted to the right and the input bit becomes 1.

To generate the same output stream, the order of the taps is the counterpart (see above) of the order for the conventional LFSR, otherwise the stream will be in reverse. Note that the internal state of the LFSR is not necessarily the same. The Galois register shown has the same output stream as the Fibonacci register in the first section.

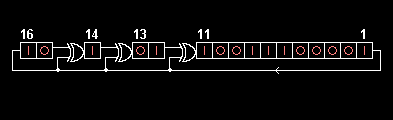
• Galois LFSRs do not concatenate every tap to produce the new input (the XOR'ing is done within the LFSR and no XOR gates are run in serial, therefore the propagation times are reduced to that of one XOR rather than a whole chain), thus it is possible for each tap to be computed in parallel, increasing the speed of execution.
• In a software implementation of an LFSR, the Galois form is more efficient as the XOR operations can be implemented a word at a time: only the output bit must be examined individually.

Below is a code example of a 32-bit maximal period Galois LFSR that is valid in C

C (programming language)

C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....

:

1. include

uint32_t lfsr = 1;
unsigned period = 0;

do {
/* taps: 32 31 29 1; characteristic polynomial: x^32 + x^31 + x^29 + x + 1 */
lfsr = (lfsr >> 1) ^ (-(lfsr & 1u) & 0xD0000001u);
++period;
} while(lfsr != 1u);


And here is the code for the 16 bit example in the figure

1. include

uint16_t lfsr = 0xACE1u;
unsigned period = 0;

do {
/* taps: 16 14 13 11; characteristic polynomial: x^16 + x^14 + x^13 + x^11 + 1 */
lfsr = (lfsr >> 1) ^ (-(lfsr & 1u) & 0xB400u);
++period;
} while(lfsr != 0xACE1u);


These code examples create a toggle mask to apply to the shifted value using the XOR operator. The mask is created by first removing all but the least significant bit (the output bit) of the current value. This value is then negated (two's complement

Two's complement

The two's complement of a binary number is defined as the value obtained by subtracting the number from a large power of two...

 negation), which creates a value of either all 0s or all 1s, if the output bit is 0 or 1, respectively. By ANDing the result with the tap-value (e.g., 0xB400 in the second example) before applying it as the toggle mask, it acts functionally as a conditional to either apply or not apply the toggle mask based on the output bit. A more explicit but significantly less efficient code example is shown below.

1. include

uint16_t lfsr = 0xACE1u;
unsigned period = 0;

do {
unsigned lsb = lfsr & 1; /* Get lsb (i.e., the output bit). */
lfsr >>= 1; /* Shift register */
if (lsb 1) /* Only apply toggle mask if output bit is 1. */
lfsr ^= 0xB400u; /* Apply toggle mask, value has 1 at bits corresponding
* to taps, 0 elsewhere. */
++period;
} while(lfsr != 0xACE1u);

Non-binary Galois LFSR

Binary Galois LFSRs like the ones shown above can be generalized to any q-ary alphabet {0, 1, ... , q − 1} (e.g., for binary, q is equal to two, and the alphabet is simply {0, 1}). In this case, the exclusive-or component is generalized to addition modulo

Modular arithmetic

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....

-q (note that XOR is addition modulo 2), and the feedback bit (output bit) is multiplied (modulo-q) by a q-ary value which is constant for each specific tap point. Note that this is also a generalization of the binary case, where the feedback is multiplied by either 0 (no feedback, i.e., no tap) or 1 (feedback is present). Given an appropriate tap configuration, such LFSRs can be used to generate Galois fields

Finite field

In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...

 for arbitrary values of q.
Some polynomials for maximal LFSRs
The following table lists maximal-length polynomials for shift-register lengths up to 19. Note that more than one maximal-length polynomial may exist for any given shift-register length.

Bits	Feedback polynomial	Period
n
2		3
3		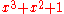7
4		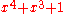15
5		31
6		63
7		127
8		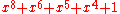255
9		511
10		1023
11		2047
12		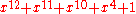4095
13		8191
14		16383
15		32767
16		65535
17		131071
18		262143
19		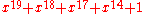524287
20 to 168	http://www.xilinx.com/support/documentation/application_notes/xapp052.pdf

Output-stream properties

• Ones and zeroes occur in 'runs'. The output stream 0110100, for example consists of five runs of lengths 1,2,1,1,2, in order. In one period of a maximal LFSR, 2^n −1 runs occur (for example, a six bit LFSR will have 32 runs). Exactly half of these runs will be one bit long, a quarter will be two bits long, up to a single run of zeroes n − 1 bits long, and a single run of ones n bits long. This distribution almost equals the statistical expectation value
  Expectation
  In the case of uncertainty, expectation is what is considered the most likely to happen. An expectation, which is a belief that is centered on the future, may or may not be realistic. A less advantageous result gives rise to the emotion of disappointment. If something happens that is not at all...
  
   for a truly random sequence. However, the probability of finding exactly this distribution in a sample of a truly random sequence is rather low.
• LFSR output streams are deterministic. If you know the present state, you can predict the next state. This is not possible with truly random events.
• The output stream is reversible; an LFSR with mirrored taps will cycle through the output sequence in reverse order.

Applications
LFSRs can be implemented in hardware, and this makes them useful in applications that require very fast generation of a pseudo-random sequence, such as direct-sequence spread spectrum

Direct-sequence spread spectrum

In telecommunications, direct-sequence spread spectrum is a modulation technique. As with other spread spectrum technologies, the transmitted signal takes up more bandwidth than the information signal that is being modulated. The name 'spread spectrum' comes from the fact that the carrier signals...

 radio. LFSRs have also been used for generating an approximation of white noise

White noise

White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...

 in various programmable sound generator

Programmable sound generator

A Programmable Sound Generator is a sound chip that generates sound waves by synthesizing multiple basic waveforms, and often some kind of noise generator, and combining and mixing these waveforms into a complex waveform, then shaping the amplitude of the resulting waveform using...

s.

Uses as counters

The repeating sequence of states of an LFSR allows it to be used as a clock divider, or as a counter when a non-binary sequence is acceptable as is often the case where computer index or framing locations need to be machine-readable. LFSR counter

Counter

In digital logic and computing, a counter is a device which stores the number of times a particular event or process has occurred, often in relationship to a clock signal.- Electronic counters :...

s have simpler feedback logic than natural binary counters or Gray code

Gray code

The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only one bit. It is a non-weighted code....

 counters, and therefore can operate at higher clock rates. However it is necessary to ensure that the LFSR never enters an all-zeros state, for example by presetting it at start-up to any other state in the sequence.
The table of primitive polynomials shows how LFSRs can be arranged in Fibonacci or Galois form to give maximal periods. One can obtain any other period by adding to an LFSR that has a longer period some logic that shortens the sequence by skipping some states.

Uses in cryptography

LFSRs have long been used as pseudo-random number generators for use in stream cipher

Stream cipher

In cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...

s (especially in military

Military

A military is an organization authorized by its greater society to use lethal force, usually including use of weapons, in defending its country by combating actual or perceived threats. The military may have additional functions of use to its greater society, such as advancing a political agenda e.g...

 cryptography

Cryptography

Cryptography is the practice and study of techniques for secure communication in the presence of third parties...

), due to the ease of construction from simple electromechanical or electronic circuits, long periods

Periodic function

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...

, and very uniformly distributed

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

 output streams. However, an LFSR is a linear system, leading to fairly easy cryptanalysis

Cryptanalysis

Cryptanalysis is the study of methods for obtaining the meaning of encrypted information, without access to the secret information that is normally required to do so. Typically, this involves knowing how the system works and finding a secret key...

. For example, given a stretch of known plaintext and corresponding ciphertext, an attacker can intercept and recover a stretch of LFSR output stream used in the system described, and from that stretch of the output stream can construct an LFSR of minimal size that simulates the intended receiver by using the Berlekamp-Massey algorithm

Berlekamp-Massey algorithm

The Berlekamp–Massey algorithm is an algorithm that will find the shortest linear feedback shift register for a given binary output sequence. The algorithm will also find the minimal polynomial of a linearly recurrent sequence in an arbitrary field....

. This LFSR can then be fed the intercepted stretch of output stream to recover the remaining plaintext.

Three general methods are employed to reduce this problem in LFSR-based stream ciphers:

• Non-linear combination of several bit
  Bit
  A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
  
  s from the LFSR state
  State (computer science)
  In computer science and automata theory, a state is a unique configuration of information in a program or machine. It is a concept that occasionally extends into some forms of systems programming such as lexers and parsers....
  
  ;
• Non-linear combination of the output bits of two or more LFSRs (see also: shrinking generator
  Shrinking generator
  In cryptography, the shrinking generator is a form of pseudorandom number generator intended to be used in a stream cipher. It was published in Crypto 1993 by Don Coppersmith, Hugo Krawczyk, and Yishay Mansour....
  
  ); or
• Irregular clocking of the LFSR, as in the alternating step generator
  Alternating step generator
  In cryptography, an alternating step generator is a cryptographic pseudorandom number generator intended to be used in a stream cipher. The design was published in 1987 by C. G. Günther...
  
  .

Important LFSR-based stream ciphers include A5/1

A5/1

A5/1 is a stream cipher used to provide over-the-air communication privacy in the GSM cellular telephone standard. It was initially kept secret, but became public knowledge through leaks and reverse engineering. A number of serious weaknesses in the cipher have been identified.-History and...

 and A5/2

A5/2

A5/2 is a stream cipher used to provide voice privacy in the GSM cellular telephone protocol.The cipher is based around a combination of four linear feedback shift registers with irregular clocking and a non-linear combiner.In 1999, Ian Goldberg and David A...

, used in GSM cell phones, E0

E0 (cipher)

E0 is a stream cipher used in the Bluetooth protocol. It generates a sequence of pseudorandom numbers and combines it with the data using the XOR operator. The key length may vary, but is generally 128 bits.-Description:...

, used in Bluetooth

Bluetooth

Bluetooth is a proprietary open wireless technology standard for exchanging data over short distances from fixed and mobile devices, creating personal area networks with high levels of security...

, and the shrinking generator

Shrinking generator

In cryptography, the shrinking generator is a form of pseudorandom number generator intended to be used in a stream cipher. It was published in Crypto 1993 by Don Coppersmith, Hugo Krawczyk, and Yishay Mansour....

. The A5/2 cipher has been broken and both A5/1 and E0 have serious weaknesses.

Scrambling

To prevent short repeating sequences (e.g., runs of 0's or 1's) from forming spectral lines that may complicate symbol tracking at the
receiver or interfere with other transmissions, linear feedback registers are often used to "randomize" the transmitted bitstream. This
randomization is removed at the receiver after demodulation.
When the LFSR runs at the same rate as the transmitted symbol stream, this technique is referred to as scrambling.
When the LFSR runs considerably faster than the symbol stream, expanding the bandwidth of the transmitted signal, this is direct-sequence spread spectrum

Direct-sequence spread spectrum

In telecommunications, direct-sequence spread spectrum is a modulation technique. As with other spread spectrum technologies, the transmitted signal takes up more bandwidth than the information signal that is being modulated. The name 'spread spectrum' comes from the fact that the carrier signals...

.

Neither scheme should be confused with encryption

Encryption

In cryptography, encryption is the process of transforming information using an algorithm to make it unreadable to anyone except those possessing special knowledge, usually referred to as a key. The result of the process is encrypted information...

 or encipherment; scrambling and spreading with LFSRs do not protect the information from eavesdropping. They are instead used to produce equivalent streams that possess convenient engineering properties to allow for robust and efficient modulation and demodulation.

Digital broadcasting systems that use linear feedback registers:

• ATSC Standards (digital TV transmission system – North America)
• DAB
  Digital audio broadcasting
  Digital Audio Broadcasting is a digital radio technology for broadcasting radio stations, used in several countries, particularly in Europe. As of 2006, approximately 1,000 stations worldwide broadcast in the DAB format....
  
   (Digital Audio Broadcasting
  Digital audio broadcasting
  Digital Audio Broadcasting is a digital radio technology for broadcasting radio stations, used in several countries, particularly in Europe. As of 2006, approximately 1,000 stations worldwide broadcast in the DAB format....
  
   system – for radio)
• DVB-T
  DVB-T
  DVB-T is an abbreviation for Digital Video Broadcasting — Terrestrial; it is the DVB European-based consortium standard for the broadcast transmission of digital terrestrial television that was first published in 1997 and first broadcast in the UK in 1998...
  
   (digital TV transmission system – Europe, Australia, parts of Asia)
• NICAM
  NICAM
  Near Instantaneous Companded Audio Multiplex is an early form of lossy compression for digital audio. It was originally developed in the early 1970s for point-to-point links within broadcasting networks...
  
   (digital audio system for television)

Other digital communications systems using LFSRs:

• IBS (INTELSAT business service)
• IDR (Intermediate Data Rate service)
• SDI
  Serial Digital Interface
  Serial digital interface is a family of video interfaces standardized by SMPTE. For example, ITU-R BT.656 and SMPTE 259M define digital video interfaces used for broadcast-grade video...
  
   (Serial Digital Interface transmission)
• Data transfer over PSTN (according to the ITU-T
  ITU-T
  The ITU Telecommunication Standardization Sector is one of the three sectors of the International Telecommunication Union ; it coordinates standards for telecommunications....
  
   V-series recommendations)
• CDMA (Code Division Multiple Access) cellular telephony
• 100BASE-T2 "fast" Ethernet scrambles bits using an LFSR
• 1000BASE-T Ethernet, the most common form of Gigabit Ethernet, scrambles bits using an LFSR
• PCI Express
  PCI Express
  PCI Express , officially abbreviated as PCIe, is a computer expansion card standard designed to replace the older PCI, PCI-X, and AGP bus standards...
  
   3.0
• SATA
  Sata
  Sata is a traditional dish from the Malaysian state of Terengganu, consisting of spiced fish meat wrapped in banana leaves and cooked on a grill.It is a type of Malaysian fish cake, or otak-otak...
  
  
• USB 3.0
  USB 3.0
  USB 3.0 is the second major revision of the Universal Serial Bus standard for computer connectivity.USB 3.0 has transmission speeds of up to 5 Gbit/s, which is 10 times faster than USB 2.0 . USB 3.0 significantly reduces the time required for data transmission, reduces power consumption, and...
  
  
• IEEE 802.11a scrambles bits using an LFSR

Other uses

The German time signal DCF77

DCF77

DCF77 is a longwave time signal and standard-frequency radio station. Its primary and backup transmitter are located in Mainflingen, about 25 km south-east of Frankfurt am Main, Germany. It is operated by Media Broadcast GmbH , on behalf of the Physikalisch-Technische Bundesanstalt, Germany's...

, in addition to amplitude keying, employs phase-shift keying

Phase-shift keying

Phase-shift keying is a digital modulation scheme that conveys data by changing, or modulating, the phase of a reference signal ....

 driven by a 9-stage LFSR to increase the accuracy of received time and the robustness of the data stream in the presence of noise.

The Global Positioning System

Global Positioning System

The Global Positioning System is a space-based global navigation satellite system that provides location and time information in all weather, anywhere on or near the Earth, where there is an unobstructed line of sight to four or more GPS satellites...

 uses an LFSR to rapidly transmit a sequence that indicates high-precision relative time offsets.
See also

• Pinwheel
  Pinwheel (cryptography)
  In cryptography, a pinwheel was a device for producing a short pseudorandom sequence of bits , as a component in a cipher machine. A pinwheel consisted of a rotating wheel with a certain number of positions on its periphery. Each position had a "pin" or "lug" which could be either "set" or "unset"...
  
  
• Mersenne twister
• Maximum length sequence
  Maximum length sequence
  A maximum length sequence is a type of pseudorandom binary sequence.They are bit sequences generated using maximal linear feedback shift registers and are so called because they are periodic and reproduce every binary sequence that can be reproduced by the shift registers...
  
  
• analog feedback shift register

External links

• LFSR Reference LFSR theory and implementation, maximal length sequences, and comprehensive feedback tables for lengths from 7 to 16,777,215 (3 to 24 stages), and partial tables for lengths up to 4,294,967,295 (25 to 32 stages).
• International Telecommunications Union Recommendation O.151 (August 1992)
• Maximal Length LFSR table with length from 2 to 67.
• Pseudo-Random Number Generation Routine
• http://www.ece.ualberta.ca/~elliott/ee552/studentAppNotes/1999f/Drivers_Ed/lfsr.html
• http://www.quadibloc.com/crypto/co040801.htm
• Simple explanation of LFSRs for Engineers
• Feedback terms
• General LFSR Theory
• An implementation of a cryptographically secure shrinking pseudorandom number generator.
• An implementation of LFSR in VHDL.
• Simple VHDL coding for Galois and Fibonacci LFSR.