
Mersenne twister
Encyclopedia
The Mersenne twister is a pseudorandom number generator
developed in 1997 by and that is based on a matrix linear recurrence over a finite binary
field
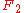 . It provides for fast generation of very high-quality pseudorandom numbers, having been designed specifically to rectify many of the flaws found in older algorithms.
. It provides for fast generation of very high-quality pseudorandom numbers, having been designed specifically to rectify many of the flaws found in older algorithms.
Its name derives from the fact that period length is chosen to be a Mersenne prime
. There are at least two common variants of the algorithm, differing only in the size of the Mersenne primes used. The newer and more commonly used one is the Mersenne Twister MT19937, with 32-bit word length. There is also a variant with 64-bit word length, MT19937-64, which generates a different sequence.
For a k-bit word length, the Mersenne Twister generates numbers with an almost uniform distribution in the range .
.
(unlike Blum Blum Shub). Observing a sufficient number of iterates (624 in the case of MT19937) allows one to predict all future iterates. A pair of cryptographic stream ciphers based on output from Mersenne twister has been proposed by Makoto Matsumoto et al. The authors claim speeds 1.5 to 2 times faster than Advanced Encryption Standard
in counter mode.
Another issue is that it can take a long time to turn a non-random initial state (notably the presence of many zeros) into output that passes randomness tests
. A small lagged Fibonacci generator
or linear congruential generator
gets started much more quickly and usually is used to seed the Mersenne Twister with random initial values.
For many applications the Mersenne twister is quickly becoming the pseudorandom number generator of choice.
The Mersenne Twister is designed with Monte Carlo simulations and other statistical simulations in mind. Researchers primarily want high quality numbers but also benefit from its speed and portability.
. These critics claim that while it is good at generating random numbers, it is not very elegant and is overly complex to implement. Marsaglia provided several examples of random number generators that are less complex yet which provide significantly larger periods. For example, a simple complementary multiply-with-carry
generator can have a period 1033000 times as long, be significantly faster, and maintain better or equal randomness.
Another issue is that Mersenne Twister is sensitive to poor initialization and can take a long time to recover from a zero-excess initial state. An alternative, WELL ("Well Equidistributed Long-period Linear"), has quicker recovery, same or better performance and equal randomness.
with the restriction that 2nw − r − 1 is a Mersenne prime. This choice simplifies the primitivity test and k-distribution test that are needed in the parameter search.
For a word x with w bit width, it is expressed as the recurrence relation
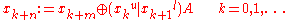
with | as the bitwise or
and as the bitwise exclusive or (XOR), xu, xl being x with upper and lower bitmasks applied. The twist transformation A is defined in rational normal form
as the bitwise exclusive or (XOR), xu, xl being x with upper and lower bitmasks applied. The twist transformation A is defined in rational normal form
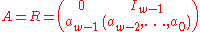
with In − 1 as the (n − 1) × (n − 1) identity matrix (and in contrast to normal matrix multiplication, bitwise XOR replaces addition). The rational normal form has the benefit that it can be efficiently expressed as
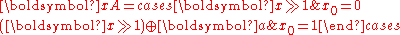
where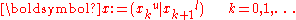
In order to achieve the 2nw − r − 1 theoretical upper limit of the period in a TGFSR, φB(t) must be a primitive polynomial
, φB(t) being the characteristic polynomial
of
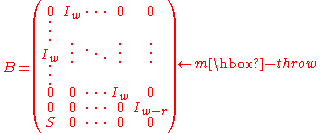
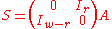
The twist transformation improves the classical GFSR with the following key properties:
As like TGFSR(R), the Mersenne Twister is cascaded with a tempering transform to compensate for the reduced dimensionality of equidistribution (because of the choice of A being in the rational normal form), which is equivalent to the transformation A = R → A = T−1RT, T invertible. The tempering is defined in the case of Mersenne Twister as
with <<, >> as the bitwise left and right shifts, and & as the bitwise and
. The first and last transforms are added in order to improve lower bit equidistribution. From the property of TGFSR,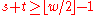 is required to reach the upper bound of equidistribution for the upper bits.
is required to reach the upper bound of equidistribution for the upper bits.
The coefficients for MT19937 are:
generates uniformly distributed 32-bit integers in the range [0, 232 − 1] with the MT19937 algorithm:
// Create a length 624 array to store the state of the generator
int[0..623] MT
int index = 0
// Initialize the generator from a seed
function initialize_generator(int seed) {
MT[0] := seed
for i from 1 to 623 { // loop over each other element
MT[i] := last 32 bits of(1812433253 * (MT[i-1] xor (right shift by 30 bits(MT[i-1]))) + i) // 0x6c078965
}
}
// Extract a tempered pseudorandom number based on the index-th value,
// calling generate_numbers every 624 numbers
function extract_number {
if index 0 {
generate_numbers
}
int y := MT[index]
y := y xor (right shift by 11 bits(y))
y := y xor (left shift by 7 bits(y) and (2636928640)) // 0x9d2c5680
y := y xor (left shift by 15 bits(y) and (4022730752)) // 0xefc60000
y := y xor (right shift by 18 bits(y))
index := (index + 1) mod
624
return y
}
// Generate an array of 624 untempered numbers
function generate_numbers {
for i from 0 to 623 {
int y := 32nd bit of(MT[i]) + last 31 bits of(MT[(i+1) mod 624])
MT[i] := MT[(i + 397) mod 624] xor (right shift by 1 bit(y))
if (y mod 2) != 0 { // y is odd
MT[i] := MT[i] xor (2567483615) // 0x9908b0df
}
}
}
SFMT
SFMT, the SIMD
-oriented Fast Mersenne Twister, is a variant of Mersenne Twister, introduced in 2006, designed to be fast when it runs on 128-bit SIMD.
Intel SSE2
and PowerPC
AltiVec are supported by SFMT. It is also used for games with the Cell BE
in the PlayStation 3
.
Implementations in various languages
External links
Pseudorandom number generator
A pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
developed in 1997 by and that is based on a matrix linear recurrence over a finite binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
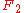 . It provides for fast generation of very high-quality pseudorandom numbers, having been designed specifically to rectify many of the flaws found in older algorithms.
. It provides for fast generation of very high-quality pseudorandom numbers, having been designed specifically to rectify many of the flaws found in older algorithms.Its name derives from the fact that period length is chosen to be a Mersenne prime
Mersenne prime
In mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
. There are at least two common variants of the algorithm, differing only in the size of the Mersenne primes used. The newer and more commonly used one is the Mersenne Twister MT19937, with 32-bit word length. There is also a variant with 64-bit word length, MT19937-64, which generates a different sequence.
For a k-bit word length, the Mersenne Twister generates numbers with an almost uniform distribution in the range
 .
.Applications
The algorithm in its native form is not suitable for cryptographyCryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
(unlike Blum Blum Shub). Observing a sufficient number of iterates (624 in the case of MT19937) allows one to predict all future iterates. A pair of cryptographic stream ciphers based on output from Mersenne twister has been proposed by Makoto Matsumoto et al. The authors claim speeds 1.5 to 2 times faster than Advanced Encryption Standard
Advanced Encryption Standard
Advanced Encryption Standard is a specification for the encryption of electronic data. It has been adopted by the U.S. government and is now used worldwide. It supersedes DES...
in counter mode.
Another issue is that it can take a long time to turn a non-random initial state (notably the presence of many zeros) into output that passes randomness tests
Randomness tests
The issue of randomness is an important philosophical and theoretical question.Many random number generators in use today generate what are called "random sequences" but they are actually the result of prescribed algorithms and so they are called pseudo-random number generators.These generators do...
. A small lagged Fibonacci generator
Lagged Fibonacci generator
A Lagged Fibonacci generator is an example of a pseudorandom number generator. This class of random number generator is aimed at being an improvement on the 'standard' linear congruential generator...
or linear congruential generator
Linear congruential generator
A Linear Congruential Generator represents one of the oldest and best-known pseudorandom number generator algorithms. The theory behind them is easy to understand, and they are easily implemented and fast....
gets started much more quickly and usually is used to seed the Mersenne Twister with random initial values.
For many applications the Mersenne twister is quickly becoming the pseudorandom number generator of choice.
The Mersenne Twister is designed with Monte Carlo simulations and other statistical simulations in mind. Researchers primarily want high quality numbers but also benefit from its speed and portability.
Advantages
The commonly used variant of Mersenne Twister, MT19937, which produces a sequence of 32-bit integers, has the following desirable properties:- It has a very long period of 219937 − 1. While a long period is not a guarantee of quality in a random number generator, short periods (such as the 232 common in many software packages) can be problematic.
- It is k-distributed to 32-bit accuracy for every 1 ≤ k ≤ 623 (see definition below).
- It passes numerous tests for statistical randomness, including the Diehard testsDiehard testsThe diehard tests are a battery of statistical tests for measuring the quality of a random number generator. They were developed by George Marsaglia over several years and first published in 1995 on a CD-ROM of random numbers.These are the tests:...
. It passes most, but not all, of the even more stringent TestU01 CrushTestU01TestU01 is a software library, implemented in the ANSI C language, and offering a collection of utilities for the empirical statistical testing of uniform random number generators....
randomness tests.
k-distribution
A pseudorandom sequence xi of w-bit integers of period P is said to be k-distributed to v-bit accuracy if the following holds.- Let truncv(x) denote the number formed by the leading v bits of x, and consider P of the kv-bit vectors
-
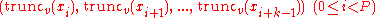 .
.
-
- Then each of the 2kv possible combinations of bits occurs the same number of times in a period, except for the all-zero combination that occurs once less often.
Alternatives
The Mersenne Twister algorithm has received some criticism in the computer science field, notably by George MarsagliaGeorge Marsaglia
George Marsaglia was an American mathematician and computer scientist. He established the lattice structure of congruential random number generators in the paper "Random numbers fall mainly in the planes". This phenomenon is sometimes called the Marsaglia effect...
. These critics claim that while it is good at generating random numbers, it is not very elegant and is overly complex to implement. Marsaglia provided several examples of random number generators that are less complex yet which provide significantly larger periods. For example, a simple complementary multiply-with-carry
Multiply-with-carry
In computer science, multiply-with-carry is a method invented by George Marsaglia for generating sequences of random integers based on an initial set of from two to many thousands of randomly chosen seed values...
generator can have a period 1033000 times as long, be significantly faster, and maintain better or equal randomness.
Another issue is that Mersenne Twister is sensitive to poor initialization and can take a long time to recover from a zero-excess initial state. An alternative, WELL ("Well Equidistributed Long-period Linear"), has quicker recovery, same or better performance and equal randomness.
Algorithmic detail
The Mersenne Twister algorithm is a twisted generalised feedback shift register (twisted GFSR, or TGFSR) of rational normal form (TGFSR(R)), with state bit reflection and tempering. It is characterized by the following quantities:- w: word size (in number of bits)
- n: degree of recurrence
- m: middle word, or the number of parallel sequences, 1 ≤ m ≤ n
- r: separation point of one word, or the number of bits of the lower bitmask, 0 ≤ r ≤ w - 1
- a: coefficients of the rational normal form twist matrix
- b, c: TGFSR(R) tempering bitmasks
- s, t: TGFSR(R) tempering bit shifts
- u, l: additional Mersenne Twister tempering bit shifts
with the restriction that 2nw − r − 1 is a Mersenne prime. This choice simplifies the primitivity test and k-distribution test that are needed in the parameter search.
For a word x with w bit width, it is expressed as the recurrence relation
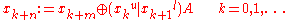
with | as the bitwise or
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
and
 as the bitwise exclusive or (XOR), xu, xl being x with upper and lower bitmasks applied. The twist transformation A is defined in rational normal form
as the bitwise exclusive or (XOR), xu, xl being x with upper and lower bitmasks applied. The twist transformation A is defined in rational normal form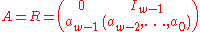
with In − 1 as the (n − 1) × (n − 1) identity matrix (and in contrast to normal matrix multiplication, bitwise XOR replaces addition). The rational normal form has the benefit that it can be efficiently expressed as
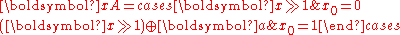
where
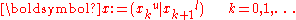
In order to achieve the 2nw − r − 1 theoretical upper limit of the period in a TGFSR, φB(t) must be a primitive polynomial
Primitive polynomial
In field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite extension field GF...
, φB(t) being the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of
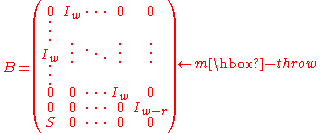
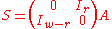
The twist transformation improves the classical GFSR with the following key properties:
- Period reaches the theoretical upper limit 2nw − r − 1 (except if initialized with 0)
- Equidistribution in n dimensions (e.g. linear congruential generatorLinear congruential generatorA Linear Congruential Generator represents one of the oldest and best-known pseudorandom number generator algorithms. The theory behind them is easy to understand, and they are easily implemented and fast....
s can at best manage reasonable distribution in 5 dimensions)
As like TGFSR(R), the Mersenne Twister is cascaded with a tempering transform to compensate for the reduced dimensionality of equidistribution (because of the choice of A being in the rational normal form), which is equivalent to the transformation A = R → A = T−1RT, T invertible. The tempering is defined in the case of Mersenne Twister as
- y := x ⊕ (x >> u)
- y := :y ⊕ ((y << s) & b)
- y := :y ⊕ ((y << t) & c)
- z := y ⊕ (y >> l)
with <<, >> as the bitwise left and right shifts, and & as the bitwise and
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
. The first and last transforms are added in order to improve lower bit equidistribution. From the property of TGFSR,
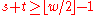 is required to reach the upper bound of equidistribution for the upper bits.
is required to reach the upper bound of equidistribution for the upper bits.The coefficients for MT19937 are:
- (w, n, m, r) = (32, 624, 397, 31)
- a = 9908B0DF16
- u = 11
- (s, b) = (7, 9D2C568016)
- (t, c) = (15, EFC6000016)
- l = 18
Pseudocode
The following piece of pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
generates uniformly distributed 32-bit integers in the range [0, 232 − 1] with the MT19937 algorithm:
// Create a length 624 array to store the state of the generator
int[0..623] MT
int index = 0
// Initialize the generator from a seed
function initialize_generator(int seed) {
MT[0] := seed
for i from 1 to 623 { // loop over each other element
MT[i] := last 32 bits of(1812433253 * (MT[i-1] xor (right shift by 30 bits(MT[i-1]))) + i) // 0x6c078965
}
}
// Extract a tempered pseudorandom number based on the index-th value,
// calling generate_numbers every 624 numbers
function extract_number {
if index 0 {
generate_numbers
}
int y := MT[index]
y := y xor (right shift by 11 bits(y))
y := y xor (left shift by 7 bits(y) and (2636928640)) // 0x9d2c5680
y := y xor (left shift by 15 bits(y) and (4022730752)) // 0xefc60000
y := y xor (right shift by 18 bits(y))
index := (index + 1) mod
Modulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
624
return y
}
// Generate an array of 624 untempered numbers
function generate_numbers {
for i from 0 to 623 {
int y := 32nd bit of(MT[i]) + last 31 bits of(MT[(i+1) mod 624])
MT[i] := MT[(i + 397) mod 624] xor (right shift by 1 bit(y))
if (y mod 2) != 0 { // y is odd
MT[i] := MT[i] xor (2567483615) // 0x9908b0df
}
}
}
SFMT
SFMT, the SIMD
SIMD
Single instruction, multiple data , is a class of parallel computers in Flynn's taxonomy. It describes computers with multiple processing elements that perform the same operation on multiple data simultaneously...
-oriented Fast Mersenne Twister, is a variant of Mersenne Twister, introduced in 2006, designed to be fast when it runs on 128-bit SIMD.
- It is roughly twice as fast as Mersenne Twister.
- It has a better equidistribution property of v-bit accuracy than MT but worse than WELL ("Well Equidistributed Long-period Linear").
- It has quicker recovery from zero-excess initial state than MT, but slower than WELL.
- It supports various periods from 2607-1 to 2216091-1.
Intel SSE2
SSE2
SSE2, Streaming SIMD Extensions 2, is one of the Intel SIMD processor supplementary instruction sets first introduced by Intel with the initial version of the Pentium 4 in 2001. It extends the earlier SSE instruction set, and is intended to fully supplant MMX. Intel extended SSE2 to create SSE3...
and PowerPC
PowerPC
PowerPC is a RISC architecture created by the 1991 Apple–IBM–Motorola alliance, known as AIM...
AltiVec are supported by SFMT. It is also used for games with the Cell BE
Cell (microprocessor)
Cell is a microprocessor architecture jointly developed by Sony, Sony Computer Entertainment, Toshiba, and IBM, an alliance known as "STI". The architectural design and first implementation were carried out at the STI Design Center in Austin, Texas over a four-year period beginning March 2001 on a...
in the PlayStation 3
PlayStation 3
The is the third home video game console produced by Sony Computer Entertainment and the successor to the PlayStation 2 as part of the PlayStation series. The PlayStation 3 competes with Microsoft's Xbox 360 and Nintendo's Wii as part of the seventh generation of video game consoles...
.
Implementations in various languages
- It also is implemented in gLibGLibGLib is a cross-platform software utility library that began as part of the GTK+ project. However, before releasing version 2 of GTK+, the project's developers decided to separate non-GUI-specific code from the GTK+ platform, thus creating GLib as a separate product...
and the standard libraries of at least PHPPHPPHP is a general-purpose server-side scripting language originally designed for web development to produce dynamic web pages. For this purpose, PHP code is embedded into the HTML source document and interpreted by a web server with a PHP processor module, which generates the web page document...
, PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
and Ruby.
External links
GLib
GLib is a cross-platform software utility library that began as part of the GTK+ project. However, before releasing version 2 of GTK+, the project's developers decided to separate non-GUI-specific code from the GTK+ platform, thus creating GLib as a separate product...
and the standard libraries of at least PHP
PHP
PHP is a general-purpose server-side scripting language originally designed for web development to produce dynamic web pages. For this purpose, PHP code is embedded into the HTML source document and interpreted by a web server with a PHP processor module, which generates the web page document...
, Python
Python (programming language)
Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
and Ruby.

