
Multilinear map
Encyclopedia
In linear algebra
, a multilinear map is a function
of several variables that is linear separately in each variable. More precisely, a multilinear map is a function
where and
and  are vector space
are vector space
s (or modules
), with the following property: for each , if all of the variables but
, if all of the variables but 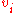 are held constant, then
are held constant, then  is a linear function of
is a linear function of  .
.
A multilinear map of two variables is a bilinear map. More generally, a multilinear map of k variables is called a k-linear map. If the codomain of a multilinear map is the field of scalars, it is called a multilinear form. Multilinear maps and multilinear forms are fundamental objects of study in multilinear algebra
.
If all variables belong to the same space, one can consider symmetric
,
antisymmetric
and alternating
k-linear maps. The latter coincide if the underlying ring
(or field) has a characteristic different from two,
else the former two coincide.

be a multilinear map between finite-dimensional vector spaces, where has dimension
has dimension 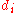 , and
, and  has dimension
has dimension  . If we choose a basis
. If we choose a basis
 for each
for each 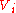 and a basis
and a basis  for
for  (using bold for vectors), then we can define a collection of scalars
(using bold for vectors), then we can define a collection of scalars  by
by
Then the scalars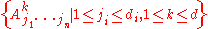 completely determine the multilinear function
completely determine the multilinear function  . In particular, if
. In particular, if
for , then
, then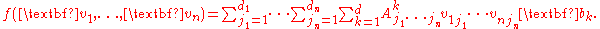

and linear maps
where denotes the tensor product
denotes the tensor product
of . The relation between the functions
. The relation between the functions  and
and  is given by the formula
is given by the formula
K with identity, as a function of the rows (or equivalently the columns) of the matrix. Let A be such a matrix and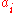 , 1 ≤ i ≤ n be the rows of A. Then the multilinear function D can be written as
, 1 ≤ i ≤ n be the rows of A. Then the multilinear function D can be written as
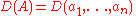
satisfying
If we let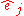 represent the jth row of the identity matrix we can express each row
represent the jth row of the identity matrix we can express each row 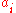 as the sum
as the sum

Using the multilinearity of D we rewrite D(A) as
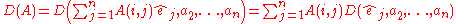
Continuing this substitution for each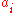 we get, for 1 ≤ i ≤ n
we get, for 1 ≤ i ≤ n
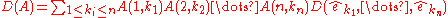
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a multilinear map is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of several variables that is linear separately in each variable. More precisely, a multilinear map is a function

where
 and
and  are vector space
are vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s (or modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
), with the following property: for each
 , if all of the variables but
, if all of the variables but 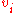 are held constant, then
are held constant, then  is a linear function of
is a linear function of  .
.A multilinear map of two variables is a bilinear map. More generally, a multilinear map of k variables is called a k-linear map. If the codomain of a multilinear map is the field of scalars, it is called a multilinear form. Multilinear maps and multilinear forms are fundamental objects of study in multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
.
If all variables belong to the same space, one can consider symmetric
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
,
antisymmetric
Antisymmetric
The word antisymmetric refers to a change to an opposite quantity when another quantity is symmetrically changed. This concept is related to that of Symmetry and Asymmetry. The difference between these three concepts can be simply illustrated with Latin letters. The character "A" is symmetric about...
and alternating
Alternating
Alternating may refer to:In mathematics:*alternating form*alternating group*alternating series*alternating knot*alternating mapIn electronics:*alternating current...
k-linear maps. The latter coincide if the underlying ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
(or field) has a characteristic different from two,
else the former two coincide.
Examples
- Any bilinear map is a multilinear map. For example, any inner product on a vector space is a multilinear map, as is the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of vectors in .
. - The determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a matrix is an antisymmetricAntisymmetricThe word antisymmetric refers to a change to an opposite quantity when another quantity is symmetrically changed. This concept is related to that of Symmetry and Asymmetry. The difference between these three concepts can be simply illustrated with Latin letters. The character "A" is symmetric about...
multilinear function of the columns (or rows) of a square matrix. - If
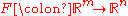 is a Ck functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
is a Ck functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, then the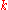 th derivative of
th derivative of  at each point
at each point  in its domain can be viewed as a symmetricSymmetric functionIn algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
in its domain can be viewed as a symmetricSymmetric functionIn algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
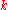 -linear function
-linear function  .
. - The tensor-to-vector projection in multilinear subspace learningMultilinear subspace learningMultilinear subspace learning aims to learn a specific small part of a large space of multidimensional objects having a particular desired property. It is a dimensionality reduction approach for finding a low-dimensional representation with certain preferred characteristics of high-dimensional...
is a multilinear map as well.
Coordinate representation
Let
be a multilinear map between finite-dimensional vector spaces, where
 has dimension
has dimension 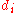 , and
, and  has dimension
has dimension  . If we choose a basis
. If we choose a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
 for each
for each 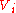 and a basis
and a basis  for
for  (using bold for vectors), then we can define a collection of scalars
(using bold for vectors), then we can define a collection of scalars  by
by
Then the scalars
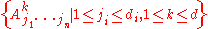 completely determine the multilinear function
completely determine the multilinear function  . In particular, if
. In particular, if
for
 , then
, then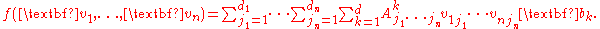
Relation to tensor products
There is a natural one-to-one correspondence between multilinear maps
and linear maps

where
 denotes the tensor product
denotes the tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of
 . The relation between the functions
. The relation between the functions  and
and  is given by the formula
is given by the formula
Multilinear functions on n×n matrices
One can consider multilinear functions, on an n×n matrix over a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
K with identity, as a function of the rows (or equivalently the columns) of the matrix. Let A be such a matrix and
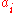 , 1 ≤ i ≤ n be the rows of A. Then the multilinear function D can be written as
, 1 ≤ i ≤ n be the rows of A. Then the multilinear function D can be written as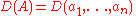
satisfying

If we let
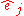 represent the jth row of the identity matrix we can express each row
represent the jth row of the identity matrix we can express each row 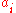 as the sum
as the sum
Using the multilinearity of D we rewrite D(A) as
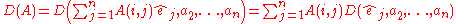
Continuing this substitution for each
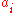 we get, for 1 ≤ i ≤ n
we get, for 1 ≤ i ≤ n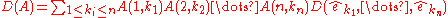
- where, since in our case
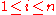
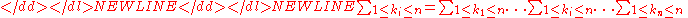
- as a series of nested summations.
Therefore, D(A) is uniquely determined by how operates on
operates on  .
.
Example
In the case of 2×2 matrices we get

Where and
and  . If we restrict D to be an alternating function then
. If we restrict D to be an alternating function then 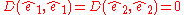 and
and 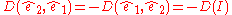 . Letting
. Letting 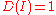 we get the determinant function on 2×2 matrices:
we get the determinant function on 2×2 matrices:

Properties
A multilinear map has a value of zero whenever one of its arguments is zero.
For n>1, the only n-linear map which is also a linear map is the zero function, see bilinear map#Examples.
See also
- Algebraic form
- Multilinear form
- Homogeneous polynomialHomogeneous polynomialIn mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
- Homogeneous functionHomogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
- TensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s - Multilinear projection

