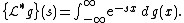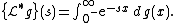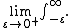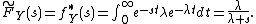Laplace-Stieltjes transform
Encyclopedia
The Laplace–Stieltjes transform, named for Pierre-Simon Laplace
and Thomas Joannes Stieltjes
, is an integral transform similar to the Laplace transform. For real-valued function
s, it is the Laplace transform of a Stieltjes measure, however it is often defined for functions with values in a Banach space
. It is useful in a number of areas of mathematics
, including functional analysis
, and certain areas of theoretical
and applied probability
.
of the form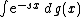
for s a complex number
. As with the usual Laplace transform, one gets a slightly different transform depending on the domain of integration, and for the integral to be defined, one also needs to require that g be of bounded variation
on the region of integration. The most common are:
The Laplace–Stieltjes transform in the case of a scalar-valued function is thus seen to be a special case of the Laplace transform of a Stieltjes measure. To wit,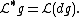
In particular, it shares many properties with the usual Laplace transform. For instance, the convolution theorem holds: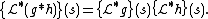
Often only real values of the variable s are considered, although if the integral exists as a proper Lebesgue integral for a given real value s = σ, then it also exists for all complex s with re(s) ≥ σ.
The Laplace–Stieltjes transform appears naturally in the following context. If X is a random variable
with cumulative distribution function
F, then the Laplace–Stieltjes transform is given by the expectation
:
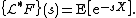
s: measures with values in a Banach space
. These are, however, important in connection with the study of semigroup
s that arise in partial differential equations, harmonic analysis
, and probability theory
. The most important semigroups are, respectively, the heat semigroup
, Riemann-Liouville semigroup, and Brownian motion
and other infinitely divisible processes.
Let g be a function from [0,∞) to a Banach space X of strongly bounded variation over every finite interval. This means that, for every fixed subinterval [0,T] one has
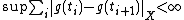
where the supremum
is taken over all partitions of [0,T]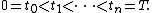
The Stieltjes integral with respect to the vector measure dg
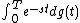
is defined as a Riemann–Stieltjes integral. Indeed, if π is the tagged partition of the interval [0,T] with subdivision , distinguished points τi∈ [ti,ti+1] and mesh size |π| = max|ti− ti+1|, the Riemann–Stieltjes integral is defined as the value of the limit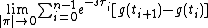
taken in the topology on X. The hypothesis of strong bounded variation guarantees convergence.
If in the topology of X the limit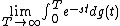
exists, then the value of this limit is the Laplace–Stieltjes transform of g.
and the Laplace transform. In particular, note the following:
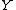the LST is,
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
and Thomas Joannes Stieltjes
Thomas Joannes Stieltjes
Thomas Joannes Stieltjes was a Dutch mathematician. He was born in Zwolle and died in Toulouse, France. He was a pioneer in the field of moment problems and contributed to the study of continued fractions....
, is an integral transform similar to the Laplace transform. For real-valued function
Real-valued function
In mathematics, a real-valued function is a function that associates to every element of the domain a real number in the image....
s, it is the Laplace transform of a Stieltjes measure, however it is often defined for functions with values in a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. It is useful in a number of areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, including functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, and certain areas of theoretical
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and applied probability
Applied probability
Much research involving probability is done under the auspices of applied probability, the application of probability theory to other scientific and engineering domains...
.
Real-valued functions
The Laplace–Stieltjes transform of a real-valued function g is given by a Lebesgue–Stieltjes integralLebesgue-Stieltjes integration
In measure-theoretic analysis and related branches of mathematics, Lebesgue–Stieltjes integration generalizes Riemann–Stieltjes and Lebesgue integration, preserving the many advantages of the former in a more general measure-theoretic framework...
of the form
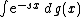
for s a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. As with the usual Laplace transform, one gets a slightly different transform depending on the domain of integration, and for the integral to be defined, one also needs to require that g be of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
on the region of integration. The most common are:
- The bilateral (or two-sided) Laplace–Stieltjes transform is given by
- The unilateral (one-sided) Laplace–Stieltjes transform is given by
-
- where the lower limit 0− means
- This is necessary to ensure that the transform captures a possible jump in g(x) at x = 0, as is needed to make sense of the Laplace transform of the Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
.
- More general transforms can be considered by integrating over a contour in the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
; see .
The Laplace–Stieltjes transform in the case of a scalar-valued function is thus seen to be a special case of the Laplace transform of a Stieltjes measure. To wit,
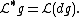
In particular, it shares many properties with the usual Laplace transform. For instance, the convolution theorem holds:
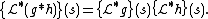
Often only real values of the variable s are considered, although if the integral exists as a proper Lebesgue integral for a given real value s = σ, then it also exists for all complex s with re(s) ≥ σ.
The Laplace–Stieltjes transform appears naturally in the following context. If X is a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
F, then the Laplace–Stieltjes transform is given by the expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
:
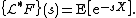
Vector measures
Whereas the Laplace–Stieltjes transform of a real-valued function is a special case of the Laplace transform of a measure applied to the associated Stieltjes measure, the conventional Laplace transform cannot handle vector measureVector measure
In mathematics, a vector measure is a function defined on a family of sets and taking vector values satisfying certain properties. It is a generalization of the concept of measure, which takes nonnegative real values only.-Definitions and first consequences:...
s: measures with values in a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. These are, however, important in connection with the study of semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s that arise in partial differential equations, harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. The most important semigroups are, respectively, the heat semigroup
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
, Riemann-Liouville semigroup, and Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
and other infinitely divisible processes.
Let g be a function from [0,∞) to a Banach space X of strongly bounded variation over every finite interval. This means that, for every fixed subinterval [0,T] one has
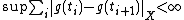
where the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
is taken over all partitions of [0,T]
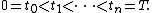
The Stieltjes integral with respect to the vector measure dg
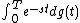
is defined as a Riemann–Stieltjes integral. Indeed, if π is the tagged partition of the interval [0,T] with subdivision , distinguished points τi∈ [ti,ti+1] and mesh size |π| = max|ti− ti+1|, the Riemann–Stieltjes integral is defined as the value of the limit
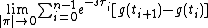
taken in the topology on X. The hypothesis of strong bounded variation guarantees convergence.
If in the topology of X the limit
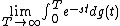
exists, then the value of this limit is the Laplace–Stieltjes transform of g.
Related transforms
The Laplace–Stieltjes transform is closely related to other integral transforms, including the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
and the Laplace transform. In particular, note the following:
- If g has derivative g' then the Laplace–Stieltjes transform of g is the Laplace transform of g' .
-
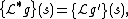
- We can obtain the Fourier–Stieltjes transform of g (and, by the above note, the Fourier transform of g' ) by
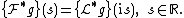
Examples
For an exponentially distributed random variable the LST is,