
Kernel (linear operator)
Encyclopedia
In linear algebra
and functional analysis
, the kernel of a linear operator L is the set of all operand
s v for which L(v) = 0. That is, if L: V → W, then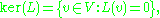
where 0 denotes the null vector
in W. The kernel of L is a linear subspace
of the domain V.
The kernel of a linear operator Rm → Rn is the same as the null space
of the corresponding n × m matrix
. Sometimes the kernel of a linear operator is referred to as the null space of the operator, and the dimension
of the kernel is referred to as the operator's nullity.
in W if and only if their difference lies in the kernel of L:
It follows that the image of L is isomorphic
to the quotient
of V by the kernel: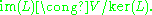
This implies the rank-nullity theorem
: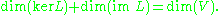
When V is an inner product space
, the quotient V / ker(L) can be identified with the orthogonal complement in V of ker(L). This is the generalization to linear operators of the row space
of a matrix.
s (and W is finite-dimensional) then a linear operator L: V → W is continuous
if and only if the kernel of L is a closed
subspace of V.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the kernel of a linear operator L is the set of all operand
Operand
In mathematics, an operand is the object of a mathematical operation, a quantity on which an operation is performed.-Example :The following arithmetic expression shows an example of operators and operands:3 + 6 = 9\;...
s v for which L(v) = 0. That is, if L: V → W, then
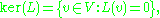
where 0 denotes the null vector
Null vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
in W. The kernel of L is a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of the domain V.
The kernel of a linear operator Rm → Rn is the same as the null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of the corresponding n × m matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Sometimes the kernel of a linear operator is referred to as the null space of the operator, and the dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of the kernel is referred to as the operator's nullity.
Examples
- If L: Rm → Rn, then the kernel of L is the solution set to a homogeneous system of linear equations. For example, if L is the operator:
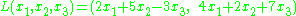
then the kernel of L is the set of solutions to the equations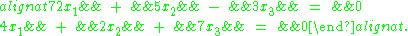
- Let C[0,1] denote the vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of all continuous real-valued functions on the interval [0,1], and define L: C[0,1] → R by the rule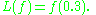
Then the kernel of L consists of all functions f ∈ C[0,1] for which f(0.3) = 0. - Let C∞(R) be the vector space of all infinitely differentiable functions R → R, and let D: C∞(R) → C∞(R) be the differentiation operatorDifferential operatorIn mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
: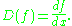
Then the kernel of D consists of all functions in C∞(R) whose derivatives are zero, i.e. the set of all constant functionConstant functionIn mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
s. - Let R∞ be the direct productDirect productIn mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of infinitely many copies of R, and let s: R∞ → R∞ be the shift operatorShift operatorIn mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....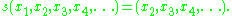
Then the kernel of s is the one-dimensional subspace consisting of all vectors (x1, 0, 0, ...). Note that s is ontoSurjective functionIn mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
, despite having nontrivial kernel. - If V is an inner product spaceInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
and W is a subspace, the kernel of the orthogonal projectionProjection (linear algebra)In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
V → W is the orthogonal complement to W in V.
Properties
If L: V → W, then two elements of V have the same imageImage (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
in W if and only if their difference lies in the kernel of L:

It follows that the image of L is isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the quotient
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
of V by the kernel:
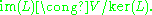
This implies the rank-nullity theorem
Rank-nullity theorem
In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
:
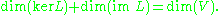
When V is an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, the quotient V / ker(L) can be identified with the orthogonal complement in V of ker(L). This is the generalization to linear operators of the row space
Row space
In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...
of a matrix.
Kernels in functional analysis
If V and W are topological vector spaceTopological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s (and W is finite-dimensional) then a linear operator L: V → W is continuous
Continuous linear operator
In functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces....
if and only if the kernel of L is a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subspace of V.
See also
- Kernel (mathematics)Kernel (mathematics)In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
- Null spaceNull spaceIn linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
- Vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
- Linear subspaceLinear subspaceThe concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
- Linear operator
- Function spaceFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
- Fredholm alternativeFredholm alternativeIn mathematics, the Fredholm alternative, named after Ivar Fredholm, is one of Fredholm's theorems and is a result in Fredholm theory. It may be expressed in several ways, as a theorem of linear algebra, a theorem of integral equations, or as a theorem on Fredholm operators...

