
Johannes De Groot
Encyclopedia
Johannes de Groot was a Dutch
mathematician
, the leading Dutch topologist
for more than two decades following World War II
.
, the Netherlands, on May 7, 1914.
He did both his undergraduate and graduate studies at the Rijksuniversiteit Groningen, where he received his Ph.D. in 1942 under the supervision of Gerrit Schaake. He studied mathematics, physics and philosophy as an undergraduate, and began his graduate studies concentrating in algebra
and algebraic geometry
, but switched to point set topology, the subject of his thesis, despite the general disinterest in the subject in the Netherlands at the time after Brouwer
, the Dutch giant in that field, had left it in favor of intuitionism
. For several years after leaving the university, De Groot taught mathematics at the secondary school level, but in 1946 he was appointed to the Mathematisch Centrum in Amsterdam
, in 1947 he began a lecturership at the University of Amsterdam, in 1948 he moved to a position as professor of mathematics at the Delft University of Technology
, and in 1952 he moved again back to the University of Amsterdam, where he remained for the rest of his life. He was head of pure mathematics at the Mathematisch Centrum from 1960 to 1964, and dean of science at Amsterdam University from 1964 on. He also visited Purdue University
(1959–1960), Washington University, St. Louis (1963–1964), the University of Florida
(1966–1967 and winters thereafter), and the University of South Florida
(1971–1972). He died on September 11, 1972.
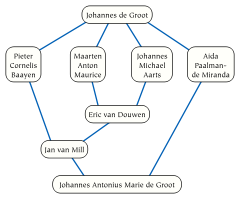 De Groot had many students, and over 100 academic descendants; Koetsier and van Mill write that many of these younger topologists experienced compactification
De Groot had many students, and over 100 academic descendants; Koetsier and van Mill write that many of these younger topologists experienced compactification
at first hand while trying to squeeze into the back seat of De Groot's small Mercedes. McDowell writes, "His students essentially constitute the topology faculties at the Dutch universities." The deep influence of de Groot on Dutch topology may be seen in the complex academic genealogy
of his namesake Johannes Antonius Marie de Groot (shown in the illustration): the later de Groot, a 1990 Ph.D. in topology, is the senior de Groot's academic grandchild, great-grandchild, and great-great-grandchild via four different paths of academic supervision.
De Groot was elected in 1969 to the Royal Dutch Academy of Sciences.
and topological group theory
, although he also made contributions to abstract algebra
and mathematical analysis
.
He wrote several papers on dimension theory
(a topic that had also been of interest to Brouwer). His first work on this subject, in his thesis, concerned the compactness degree of a space: this is a number, defined to be −1 for a compact space
, and 1 + x if every point in the space has a neighbourhood
the boundary of which has compactness degree x. He made an important conjecture, only solved much later in 1982 by Pol and 1988 by Kimura, that the compactness degree was the same as the minimum dimension of a set that could be adjoined to the space to compactify
it. Thus, for instance the familiar Euclidean space
has compactness degree zero; it is not compact itself, but every point has a neighborhood bounded by a compact sphere. This compactness degree, zero, equals the dimension of the single point that may be added to Euclidean space to form its one-point compactification. A detailed review of de Groot's compactness degree problem and its relation to other definitions of dimension for topological spaces is provided by Koetsier and van Mill
In 1959 his work on the classification of homeomorphism
s led to the theorem that one can find a large cardinal number
, ℶ2
, of pairwise non-homeomorphic
connected subsets of the Euclidean plane, such that none of these sets has any nontrivial continuous function
mapping it into itself or any other of these sets. The topological spaces formed by these subsets of the plane thus have a trivial automorphism
group; de Groot used this construction to show that all groups are the automorphism group of some compact Hausdorff space
, by replacing the edges of a Cayley graph
of the group by spaces with no nontrivial automorphisms and then applying the Stone–Čech compactification
. A related algebraic result is that every group is the automorphism group of a commutative ring
.
Other results in his research include a proof that a metrizable topological space has a non-Archimedean metric (satisfying the strong triangle inequality d(x,z) ≤ max(d(x,y),d(y,z)) if and only if it has dimension zero, description of topologically complete spaces in terms of cocompactness, and a topological characterization of Hilbert space
. From 1962 onwards, his research primarily concerned the development of new topological theories: subcompactness, cocompactness, cotopology, GA-compactification, superextension, minusspaces, antispaces, and squarecompactness.
Netherlands
The Netherlands is a constituent country of the Kingdom of the Netherlands, located mainly in North-West Europe and with several islands in the Caribbean. Mainland Netherlands borders the North Sea to the north and west, Belgium to the south, and Germany to the east, and shares maritime borders...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, the leading Dutch topologist
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
for more than two decades following World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
.
Biography
De Groot was born at Garrelsweer, a tiny village in the municipality of LoppersumLoppersum
Loppersum is a municipality and a town in the northeastern Netherlands in the province of Groningen.- Population centres :Eekwerd, Eekwerderdraai, Eenum, Fraamklap, Garrelsweer, Garsthuizen, Hoeksmeer, Honderd, Huizinge, Kolhol, Leermens, Loppersum, Lutjerijp, Lutjewijtwerd, Merum, Middelstum,...
, the Netherlands, on May 7, 1914.
He did both his undergraduate and graduate studies at the Rijksuniversiteit Groningen, where he received his Ph.D. in 1942 under the supervision of Gerrit Schaake. He studied mathematics, physics and philosophy as an undergraduate, and began his graduate studies concentrating in algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, but switched to point set topology, the subject of his thesis, despite the general disinterest in the subject in the Netherlands at the time after Brouwer
Luitzen Egbertus Jan Brouwer
Luitzen Egbertus Jan Brouwer FRS , usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, a graduate of the University of Amsterdam, who worked in topology, set theory, measure theory and complex analysis.-Biography:Early in his career,...
, the Dutch giant in that field, had left it in favor of intuitionism
Intuitionism
In the philosophy of mathematics, intuitionism, or neointuitionism , is an approach to mathematics as the constructive mental activity of humans. That is, mathematics does not consist of analytic activities wherein deep properties of existence are revealed and applied...
. For several years after leaving the university, De Groot taught mathematics at the secondary school level, but in 1946 he was appointed to the Mathematisch Centrum in Amsterdam
Amsterdam
Amsterdam is the largest city and the capital of the Netherlands. The current position of Amsterdam as capital city of the Kingdom of the Netherlands is governed by the constitution of August 24, 1815 and its successors. Amsterdam has a population of 783,364 within city limits, an urban population...
, in 1947 he began a lecturership at the University of Amsterdam, in 1948 he moved to a position as professor of mathematics at the Delft University of Technology
Delft University of Technology
Delft University of Technology , also known as TU Delft, is the largest and oldest Dutch public technical university, located in Delft, Netherlands...
, and in 1952 he moved again back to the University of Amsterdam, where he remained for the rest of his life. He was head of pure mathematics at the Mathematisch Centrum from 1960 to 1964, and dean of science at Amsterdam University from 1964 on. He also visited Purdue University
Purdue University
Purdue University, located in West Lafayette, Indiana, U.S., is the flagship university of the six-campus Purdue University system. Purdue was founded on May 6, 1869, as a land-grant university when the Indiana General Assembly, taking advantage of the Morrill Act, accepted a donation of land and...
(1959–1960), Washington University, St. Louis (1963–1964), the University of Florida
University of Florida
The University of Florida is an American public land-grant, sea-grant, and space-grant research university located on a campus in Gainesville, Florida. The university traces its historical origins to 1853, and has operated continuously on its present Gainesville campus since September 1906...
(1966–1967 and winters thereafter), and the University of South Florida
University of South Florida
The University of South Florida, also known as USF, is a member institution of the State University System of Florida, one of the state's three flagship universities for public research, and is located in Tampa, Florida, USA...
(1971–1972). He died on September 11, 1972.

Compactification
Compactification may refer to:* Compactification , making a topological space compact* Compactification , the "curling up" of extra dimensions in string theory* Compaction...
at first hand while trying to squeeze into the back seat of De Groot's small Mercedes. McDowell writes, "His students essentially constitute the topology faculties at the Dutch universities." The deep influence of de Groot on Dutch topology may be seen in the complex academic genealogy
Academic genealogy
An academic, or scientific, genealogy, organizes a family tree of scientists and scholars according to dissertation supervision relationships....
of his namesake Johannes Antonius Marie de Groot (shown in the illustration): the later de Groot, a 1990 Ph.D. in topology, is the senior de Groot's academic grandchild, great-grandchild, and great-great-grandchild via four different paths of academic supervision.
De Groot was elected in 1969 to the Royal Dutch Academy of Sciences.
Research
De Groot published approximately 90 scientific papers. His mathematical research concerned, in general, topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and topological group theory
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
, although he also made contributions to abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
.
He wrote several papers on dimension theory
Dimension theory
In mathematics, dimension theory is a branch of general topology dealing with dimensional invariants of topological spaces.-See also:*Lebesgue covering dimension*Inductive dimensions *Dimension...
(a topic that had also been of interest to Brouwer). His first work on this subject, in his thesis, concerned the compactness degree of a space: this is a number, defined to be −1 for a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, and 1 + x if every point in the space has a neighbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
the boundary of which has compactness degree x. He made an important conjecture, only solved much later in 1982 by Pol and 1988 by Kimura, that the compactness degree was the same as the minimum dimension of a set that could be adjoined to the space to compactify
Compactification (mathematics)
In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
it. Thus, for instance the familiar Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
has compactness degree zero; it is not compact itself, but every point has a neighborhood bounded by a compact sphere. This compactness degree, zero, equals the dimension of the single point that may be added to Euclidean space to form its one-point compactification. A detailed review of de Groot's compactness degree problem and its relation to other definitions of dimension for topological spaces is provided by Koetsier and van Mill
In 1959 his work on the classification of homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s led to the theorem that one can find a large cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
, ℶ2
Beth number
In mathematics, the infinite cardinal numbers are represented by the Hebrew letter \aleph indexed with a subscript that runs over the ordinal numbers...
, of pairwise non-homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
connected subsets of the Euclidean plane, such that none of these sets has any nontrivial continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
mapping it into itself or any other of these sets. The topological spaces formed by these subsets of the plane thus have a trivial automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
group; de Groot used this construction to show that all groups are the automorphism group of some compact Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, by replacing the edges of a Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of the group by spaces with no nontrivial automorphisms and then applying the Stone–Čech compactification
Stone–Cech compactification
In the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
. A related algebraic result is that every group is the automorphism group of a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
.
Other results in his research include a proof that a metrizable topological space has a non-Archimedean metric (satisfying the strong triangle inequality d(x,z) ≤ max(d(x,y),d(y,z)) if and only if it has dimension zero, description of topologically complete spaces in terms of cocompactness, and a topological characterization of Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. From 1962 onwards, his research primarily concerned the development of new topological theories: subcompactness, cocompactness, cotopology, GA-compactification, superextension, minusspaces, antispaces, and squarecompactness.
External links
- Johannes de Groot (1914–1972). Jan van Mill, Biografisch Woordenboek von Nederlandse Wiskundigen, September 2006. (In Dutch.)

