
Jamshid al-Kashi
Encyclopedia
Ghiyāth al-Dīn Jamshīd Masʾūd al-Kāshī (or al-Kāshānī) ( Qiyās-ud-din Jamshid Kāshānī) (c. 1380 Kashan
, Iran
– 22 June 1429 Samarkand
, Transoxania) was a Persian
astronomer
and mathematician
.
, in central Iran. This region was controlled by Tamurlane
, better known as Timur. Al-Kashi lived in poverty during his childhood and the beginning years of his adulthood.
The situation changed for the better when Timur died in 1405, and his son, Shah Rokh
, ascended into power. Shah Rokh and his wife, Goharshad
, a Persian princess, were very interested in the sciences, and they encouraged their court to study the various fields in great depth. Their son, Ulugh Beg
, was enthusiastic about science as well, and made some noted contributions in mathematics and astronomy himself. Consequently, the period of their power became one of many scholarly accomplishments. This was the perfect environment for al-Kashi to begin his career as one of the world’s greatest mathematicians.
Eight years after he came into power in 1409, Ulugh Beg founded an institute in Samarkand
which soon became a prominent university. Students from all over the Middle East
, and beyond, flocked to this academy in the capital city of Ulugh Beg’s empire. Consequently, Ulugh Beg harvested many great mathematicians and scientists of the Muslim world
. In 1414, al-Kashi took this opportunity to contribute vast amounts of knowledge to his people. His best work was done in the court of Ulugh Beg, and it is said that he was the king’s favourite student.
Al-Kashi was still working on his book, called “Risala al-watar wa’l-jaib” meaning “The Treatise on the Chord and Sine”, when he died in 1429. Some scholars believe that Ulugh Beg may have ordered his murder, while others say he died a natural death. The details are unclear.
entitled the Khaqani Zij, which was based on Nasir al-Din al-Tusi
's earlier Zij-i Ilkhani
. In his Khaqani Zij, al-Kashi thanks the Timurid
sultan and mathematician-astronomer Ulugh Beg
, who invited al-Kashi to work at his observatory
(see Islamic astronomy
) and his university
(see Madrasah
) which taught Islamic theology
as well as Islamic science
. Al-Kashi produced sine tables to four sexagesimal digits (equivalent to eight decimal
places) of accuracy for each degree and includes differences for each minute. He also produced tables dealing with transformations between coordinate system
s on the celestial sphere
, such as the transformation from the ecliptic coordinate system
to the equatorial coordinate system
.
on the resolution of difficulties met by predecessors in the determination of distances and sizes of heavenly bodies
such as the Earth
, the Moon
, the Sun
and the Stars.
and armillary sphere
, the equinoctial
armillary and solsticial
armillary of Mo'ayyeduddin Urdi
, the sine
and versine
instrument of Urdi, the sextant
of al-Khujandi
, the Fakhri sextant at the Samarqand observatory, a double quadrant Azimuth-altitude
instrument he invented, and a small armillary sphere incorporating an alhidade
which he invented.
instrument used to determine the time of day at which planetary conjunctions will occur, and for performing linear interpolation
.
which he called the Plate of Zones, which could graphically solve a number of planetary problems, including the prediction of the true positions in longitude
of the Sun
and Moon
, and the planet
s in terms of elliptical orbits; the latitude
s of the Sun, Moon, and planets; and the ecliptic
of the Sun. The instrument also incorporated an alhidade
and ruler
.
, the law of cosines
is named Théorème d'Al-Kashi (Theorem of Al-Kashi), as al-Kashi was the first to provide an explicit statement of the law of cosines in a form suitable for triangulation
.
and numerical analysis
, he developed an iterative method
for solving cubic equations, which was not discovered in Europe until centuries later.
A method algebraically equivalent to Newton's method
was known to his predecessor Sharaf al-Dīn al-Tūsī. Al-Kāshī improved on this by using a form of Newton's method to solve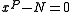 to find roots of N. In western Europe
to find roots of N. In western Europe
, a similar method was later described by Henry Biggs in his Trigonometria Britannica, published in 1633.
In order to determine sin 1°, al-Kashi discovered the following formula often attributed to François Viète
in the 16th century:
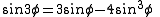
, he correctly computed 2π to 9 sexagesimal digits. This approximation of 2π is equivalent to 16 decimal
places of accuracy. This was far more accurate than the estimates earlier given in Greek mathematics
(3 decimal places by Archimedes
), Chinese mathematics
(7 decimal places by Zu Chongzhi
) or Indian mathematics
(11 decimal places by Madhava of Sangamagrama
). The accuracy of al-Kashi's estimate was not surpassed until Ludolph van Ceulen
computed 20 decimal places of π nearly 200 years later.
states that (p. 7):
, known in Persia as "Khayyam's triangle" (named after Omar Khayyám
), Struik notes that (p. 21):
Kashan
Kashan is a city in and the capital of Kashan County, in the province of Isfahan, Iran. At the 2006 census, its population was 248,789, in 67,464 families....
, Iran
Iran
Iran , officially the Islamic Republic of Iran , is a country in Southern and Western Asia. The name "Iran" has been in use natively since the Sassanian era and came into use internationally in 1935, before which the country was known to the Western world as Persia...
– 22 June 1429 Samarkand
Samarkand
Although a Persian-speaking region, it was not united politically with Iran most of the times between the disintegration of the Seleucid Empire and the Arab conquest . In the 6th century it was within the domain of the Turkic kingdom of the Göktürks.At the start of the 8th century Samarkand came...
, Transoxania) was a Persian
Persian people
The Persian people are part of the Iranian peoples who speak the modern Persian language and closely akin Iranian dialects and languages. The origin of the ethnic Iranian/Persian peoples are traced to the Ancient Iranian peoples, who were part of the ancient Indo-Iranians and themselves part of...
astronomer
Islamic astronomy
Islamic astronomy or Arabic astronomy comprises the astronomical developments made in the Islamic world, particularly during the Islamic Golden Age , and mostly written in the Arabic language. These developments mostly took place in the Middle East, Central Asia, Al-Andalus, and North Africa, and...
and mathematician
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
.
Biography
Al-Kashi was one of the best mathematicians in the Islamic world. He was born in 1380, in KashanKashan
Kashan is a city in and the capital of Kashan County, in the province of Isfahan, Iran. At the 2006 census, its population was 248,789, in 67,464 families....
, in central Iran. This region was controlled by Tamurlane
Timur
Timur , historically known as Tamerlane in English , was a 14th-century conqueror of West, South and Central Asia, and the founder of the Timurid dynasty in Central Asia, and great-great-grandfather of Babur, the founder of the Mughal Dynasty, which survived as the Mughal Empire in India until...
, better known as Timur. Al-Kashi lived in poverty during his childhood and the beginning years of his adulthood.
The situation changed for the better when Timur died in 1405, and his son, Shah Rokh
Shah Rukh (Timurid dynasty)
Shāhrukh Mīrzā was the ruler of the eastern portion of the empire established by the Central Asian warlord Timur - the founder of the Timurid dynasty - governing most of Persia and Transoxiana between 1405 and 1447...
, ascended into power. Shah Rokh and his wife, Goharshad
Goharshad
Goharshād was a wife of Shāh Rukh, the emperor of the Timurid Dynasty of Herāt. She was the daughter of Giāth ud-Din Tarkhān, an important and influential noble during Tīmur's reign...
, a Persian princess, were very interested in the sciences, and they encouraged their court to study the various fields in great depth. Their son, Ulugh Beg
Ulugh Beg
Ulugh Bek was a Timurid ruler as well as an astronomer, mathematician and sultan. His commonly-known name is not truly a personal name, but rather a moniker, which can be loosely translated as "Great Ruler" or "Patriarch Ruler" and was the Turkic equivalent of Timur's Perso-Arabic title Amīr-e...
, was enthusiastic about science as well, and made some noted contributions in mathematics and astronomy himself. Consequently, the period of their power became one of many scholarly accomplishments. This was the perfect environment for al-Kashi to begin his career as one of the world’s greatest mathematicians.
Eight years after he came into power in 1409, Ulugh Beg founded an institute in Samarkand
Samarkand
Although a Persian-speaking region, it was not united politically with Iran most of the times between the disintegration of the Seleucid Empire and the Arab conquest . In the 6th century it was within the domain of the Turkic kingdom of the Göktürks.At the start of the 8th century Samarkand came...
which soon became a prominent university. Students from all over the Middle East
Middle East
The Middle East is a region that encompasses Western Asia and Northern Africa. It is often used as a synonym for Near East, in opposition to Far East...
, and beyond, flocked to this academy in the capital city of Ulugh Beg’s empire. Consequently, Ulugh Beg harvested many great mathematicians and scientists of the Muslim world
Muslim world
The term Muslim world has several meanings. In a religious sense, it refers to those who adhere to the teachings of Islam, referred to as Muslims. In a cultural sense, it refers to Islamic civilization, inclusive of non-Muslims living in that civilization...
. In 1414, al-Kashi took this opportunity to contribute vast amounts of knowledge to his people. His best work was done in the court of Ulugh Beg, and it is said that he was the king’s favourite student.
Al-Kashi was still working on his book, called “Risala al-watar wa’l-jaib” meaning “The Treatise on the Chord and Sine”, when he died in 1429. Some scholars believe that Ulugh Beg may have ordered his murder, while others say he died a natural death. The details are unclear.
Khaqani Zij
Al-Kashi produced a ZijZij
Zīj is the generic name applied to Islamic astronomical books that tabulate parameters used for astronomical calculations of the positions of the Sun, Moon, stars, and planets. The name is derived from the Middle Persian term zih or zīg, meaning cord...
entitled the Khaqani Zij, which was based on Nasir al-Din al-Tusi
Nasir al-Din al-Tusi
Khawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...
's earlier Zij-i Ilkhani
Zij-i Ilkhani
Zīj-i Īlkhānī or Ilkhanic Tables is a Zij book with astronomical tables of planetary movements. It was compiled by the Persian astronomer Nasir al-Din al-Tusi in collaboration with his research team of astronomers at the Maragha observatory...
. In his Khaqani Zij, al-Kashi thanks the Timurid
Timurid Dynasty
The Timurids , self-designated Gurkānī , were a Persianate, Central Asian Sunni Muslim dynasty of Turko-Mongol descent whose empire included the whole of Iran, modern Afghanistan, and modern Uzbekistan, as well as large parts of contemporary Pakistan, North India, Mesopotamia, Anatolia and the...
sultan and mathematician-astronomer Ulugh Beg
Ulugh Beg
Ulugh Bek was a Timurid ruler as well as an astronomer, mathematician and sultan. His commonly-known name is not truly a personal name, but rather a moniker, which can be loosely translated as "Great Ruler" or "Patriarch Ruler" and was the Turkic equivalent of Timur's Perso-Arabic title Amīr-e...
, who invited al-Kashi to work at his observatory
Observatory
An observatory is a location used for observing terrestrial or celestial events. Astronomy, climatology/meteorology, geology, oceanography and volcanology are examples of disciplines for which observatories have been constructed...
(see Islamic astronomy
Islamic astronomy
Islamic astronomy or Arabic astronomy comprises the astronomical developments made in the Islamic world, particularly during the Islamic Golden Age , and mostly written in the Arabic language. These developments mostly took place in the Middle East, Central Asia, Al-Andalus, and North Africa, and...
) and his university
University
A university is an institution of higher education and research, which grants academic degrees in a variety of subjects. A university is an organisation that provides both undergraduate education and postgraduate education...
(see Madrasah
Madrasah
Madrasah is the Arabic word for any type of educational institution, whether secular or religious...
) which taught Islamic theology
Kalam
ʿIlm al-Kalām is the Islamic philosophical discipline of seeking theological principles through dialectic. Kalām in Islamic practice relates to the discipline of seeking theological knowledge through debate and argument. A scholar of kalām is referred to as a mutakallim...
as well as Islamic science
Islamic science
Science in the medieval Islamic world, also known as Islamic science or Arabic science, is the science developed and practised in the Islamic world during the Islamic Golden Age . During this time, Indian, Iranian and especially Greek knowledge was translated into Arabic...
. Al-Kashi produced sine tables to four sexagesimal digits (equivalent to eight decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
places) of accuracy for each degree and includes differences for each minute. He also produced tables dealing with transformations between coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
s on the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
, such as the transformation from the ecliptic coordinate system
Ecliptic coordinate system
The ecliptic coordinate system is a celestial coordinate system that uses the ecliptic for its fundamental plane. The ecliptic is the path that the sun appears to follow across the celestial sphere over the course of a year. It is also the intersection of the Earth's orbital plane and the celestial...
to the equatorial coordinate system
Equatorial coordinate system
The equatorial coordinate system is a widely-used method of mapping celestial objects. It functions by projecting the Earth's geographic poles and equator onto the celestial sphere. The projection of the Earth's equator onto the celestial sphere is called the celestial equator...
.
Astronomical Treatise on the size and distance of heavenly bodies
He wrote the book Sullam al-SamaSullam al-Sama
Sullam al-Sama also known as Resaleh-ye Kamaliyyeh meaning "The Ladder of the Sky" and also "The Stairway of Heaven" is an astronomical treatise written by Persian mathematician and astronomer Jamshid Kashani in 1407 about the determination of distance and size of the heavenly bodies such as the...
on the resolution of difficulties met by predecessors in the determination of distances and sizes of heavenly bodies
Astronomical object
Astronomical objects or celestial objects are naturally occurring physical entities, associations or structures that current science has demonstrated to exist in the observable universe. The term astronomical object is sometimes used interchangeably with astronomical body...
such as the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
, the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
, the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
and the Stars.
Treatise on Astronomical Observational Instruments
In 1416, al-Kashi wrote the Treatise on Astronomical Observational Instruments, which described a variety of different instruments, including the triquetrumTriquetrum (astronomy)
The triquetrum was the medieval name for an ancient astronomical instrument first described by Ptolemy in the Almagest . Also known as Parallactic Rulers, it was used for determining altitudes of heavenly bodies...
and armillary sphere
Armillary sphere
An armillary sphere is a model of objects in the sky , consisting of a spherical framework of rings, centred on Earth, that represent lines of celestial longitude and latitude and other astronomically important features such as the ecliptic...
, the equinoctial
Equinox
An equinox occurs twice a year, when the tilt of the Earth's axis is inclined neither away from nor towards the Sun, the center of the Sun being in the same plane as the Earth's equator...
armillary and solsticial
Solstice
A solstice is an astronomical event that happens twice each year when the Sun's apparent position in the sky, as viewed from Earth, reaches its northernmost or southernmost extremes...
armillary of Mo'ayyeduddin Urdi
Mo'ayyeduddin Urdi
Mu’ayyad al-Din al-’Urdi was an Kurdish Muslim astronomer, mathematician, architect and engineer working at the Maragheh observatory...
, the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
and versine
Versine
The versine or versed sine, versin, is a trigonometric function equal to and 2sin2. It appeared in some of the earliest trigonometric tables and was once widespread, but it is now little-used...
instrument of Urdi, the sextant
Sextant (astronomical)
Sextants for astronomical observations were used primarily for measuring the positions of stars. They are little used today, having been replaced over time by transit telescopes, astrometry techniques, and satellites such as Hipparcos....
of al-Khujandi
Al-Khujandi
Abu Mahmud Hamid ibn Khidr Khojandi was a Persian astronomer and mathematician who lived in the late 10th century and helped build an observatory near the city of Ray in Iran...
, the Fakhri sextant at the Samarqand observatory, a double quadrant Azimuth-altitude
Altitude
Altitude or height is defined based on the context in which it is used . As a general definition, altitude is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The reference datum also often varies according to the context...
instrument he invented, and a small armillary sphere incorporating an alhidade
Alhidade
An alidade is a device that allows one to sight a distant object and use the line of sight to perform a task. This task can be, for example, to draw a line on a plane table in the direction of the object or to measure the angle to the object from some reference point...
which he invented.
Plate of Conjunctions
Al-Kashi invented the Plate of Conjunctions, an analog computingAnalog computer
An analog computer is a form of computer that uses the continuously-changeable aspects of physical phenomena such as electrical, mechanical, or hydraulic quantities to model the problem being solved...
instrument used to determine the time of day at which planetary conjunctions will occur, and for performing linear interpolation
Linear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
.
Planetary computer
Al-Kashi also invented a mechanical planetary computerAnalog computer
An analog computer is a form of computer that uses the continuously-changeable aspects of physical phenomena such as electrical, mechanical, or hydraulic quantities to model the problem being solved...
which he called the Plate of Zones, which could graphically solve a number of planetary problems, including the prediction of the true positions in longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
of the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
and Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
, and the planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s in terms of elliptical orbits; the latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
s of the Sun, Moon, and planets; and the ecliptic
Ecliptic
The ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
of the Sun. The instrument also incorporated an alhidade
Alhidade
An alidade is a device that allows one to sight a distant object and use the line of sight to perform a task. This task can be, for example, to draw a line on a plane table in the direction of the object or to measure the angle to the object from some reference point...
and ruler
Ruler
A ruler, sometimes called a rule or line gauge, is an instrument used in geometry, technical drawing, printing and engineering/building to measure distances and/or to rule straight lines...
.
Law of cosines
In FrenchFrench language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
, the law of cosines
Law of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
is named Théorème d'Al-Kashi (Theorem of Al-Kashi), as al-Kashi was the first to provide an explicit statement of the law of cosines in a form suitable for triangulation
Triangulation
In trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly...
.
The Treatise on the Chord and Sine
In The Treatise on the Chord and Sine, al-Kashi computed sin 1° to nearly as much accuracy as his value for π, which was the most accurate approximation of sin 1° in his time and was not surpassed until Taqi al-Din in the 16th century. In algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, he developed an iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
for solving cubic equations, which was not discovered in Europe until centuries later.
A method algebraically equivalent to Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
was known to his predecessor Sharaf al-Dīn al-Tūsī. Al-Kāshī improved on this by using a form of Newton's method to solve
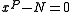 to find roots of N. In western Europe
to find roots of N. In western EuropeWestern Europe
Western Europe is a loose term for the collection of countries in the western most region of the European continents, though this definition is context-dependent and carries cultural and political connotations. One definition describes Western Europe as a geographic entity—the region lying in the...
, a similar method was later described by Henry Biggs in his Trigonometria Britannica, published in 1633.
In order to determine sin 1°, al-Kashi discovered the following formula often attributed to François Viète
François Viète
François Viète , Seigneur de la Bigotière, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to its innovative use of letters as parameters in equations...
in the 16th century:
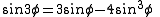
Computation of 2π
In one of his numerical approximations of πNumerical approximations of π
This page is about the history of approximations for the mathematical constant pi . There is a table summarizing the chronology of computation of π. See also the history of pi for other aspects of the evolution of our knowledge about mathematical properties of pi...
, he correctly computed 2π to 9 sexagesimal digits. This approximation of 2π is equivalent to 16 decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
places of accuracy. This was far more accurate than the estimates earlier given in Greek mathematics
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
(3 decimal places by Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
), Chinese mathematics
Chinese mathematics
Mathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry....
(7 decimal places by Zu Chongzhi
Zu Chongzhi
Zu Chongzhi , courtesy name Wenyuan , was a prominent Chinese mathematician and astronomer during the Liu Song and Southern Qi Dynasties.-Life and works:...
) or Indian mathematics
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
(11 decimal places by Madhava of Sangamagrama
Madhava of Sangamagrama
Mādhava of Sañgamāgrama was a prominent Kerala mathematician-astronomer from the town of Irińńālakkuţa near Cochin, Kerala, India. He is considered the founder of the Kerala School of Astronomy and Mathematics...
). The accuracy of al-Kashi's estimate was not surpassed until Ludolph van Ceulen
Ludolph van Ceulen
Ludolph van Ceulen was a German / Dutch mathematician from Hildesheim. He emigrated to the Netherlands....
computed 20 decimal places of π nearly 200 years later.
Decimal fractions
In discussing decimal fractions, StruikDirk Jan Struik
Dirk Jan Struik was a Dutch mathematician and Marxian theoretician who spent most of his life in the United States.- Life :...
states that (p. 7):
"The introduction of decimal fractions as a common computational practice can be dated back to the FlemishFlemish RegionThe Flemish Region is one of the three official regions of the Kingdom of Belgium—alongside the Walloon Region and the Brussels-Capital Region. Colloquially, it is usually simply referred to as Flanders, of which it is the institutional iteration within the context of the Belgian political system...
pamphlet De Thiende, published at Leyden in 1585, together with a French translation, La Disme, by the Flemish mathematician Simon StevinSimon StevinSimon Stevin was a Flemish mathematician and military engineer. He was active in a great many areas of science and engineering, both theoretical and practical...
(1548-1620), then settled in the Northern NetherlandsNetherlandsThe Netherlands is a constituent country of the Kingdom of the Netherlands, located mainly in North-West Europe and with several islands in the Caribbean. Mainland Netherlands borders the North Sea to the north and west, Belgium to the south, and Germany to the east, and shares maritime borders...
. It is true that decimal fractions were used by the ChineseChinese mathematicsMathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry....
many centuries before Stevin and that the Persian astronomer Al-Kāshī used both decimal and sexagesimal fractions with great ease in his Key to arithmetic (Samarkand, early fifteenth century)."
Khayyam's triangle
In considering Pascal's trianglePascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
, known in Persia as "Khayyam's triangle" (named after Omar Khayyám
Omar Khayyám
Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
), Struik notes that (p. 21):
"The Pascal triangle appears for the first time (so far as we know at present) in a book of 1261 written by Yang HuiYang HuiYang Hui , courtesy name Qianguang , was a Chinese mathematician from Qiantang , Zhejiang province during the late Song Dynasty . Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting 'Yang Hui's Triangle'...
, one of the mathematicians of the Sung dynasty in ChinaChinaChinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
. The properties of binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s were discussed by the Persian mathematician Jamshid Al-Kāshī in his Key to arithmetic of c. 1425. Both in China and Persia the knowledge of these properties may be much older. This knowledge was shared by some of the RenaissanceRenaissanceThe Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
mathematicians, and we see PascalBlaise PascalBlaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
's triangle on the title page of Peter Apian's GermanGerman languageGerman is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
arithmetic of 1527. After this we find the triangle and the properties of binomial coefficients in several other authors."

