Intersection theory
Encyclopedia
In mathematics
, intersection theory is a branch of algebraic geometry
, where subvarieties are intersected on an algebraic variety
, and of algebraic topology
, where intersections are computed within the cohomology ring
. The theory for varieties is older, with roots in Bézout's theorem
on curves and elimination theory
. On the other hand the topological theory more quickly reached a definitive form.
M of dimension 2n the intersection form is defined on the nth cohomology group (what is usually called the 'middle dimension') by the evaluation of the cup product
on the fundamental class
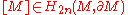. Stated precisely, there is a bilinear form
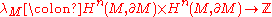
given by
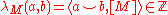
with
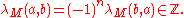
This is a symmetric form for n even, in which case the signature
of M is defined to be the signature of the form,
and an alternating form for n odd. It is possible to drop the orientability condition and work with
coefficients instead.
These forms are important topological invariants. For example, a theorem of Michael Freedman
states that simply connected compact
4-manifold
s are (almost) determined by their intersection forms up to homeomorphism
.
By Poincaré duality
, it turns out that there is a way to think of this geometrically. If possible, choose representative n-dimensional submanifolds A, B for the Poincaré duals of a and b. Then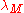
(a, b) is the oriented intersection number of A and B, which is well-defined because of the dimensions of A and B. This explains the terminology intersection form.
To give a definition, in the general case, of the intersection multiplicity was the major concern of André Weil
's 1946 book Foundations of Algebraic Geometry. Work in the 1920s of B. L. van der Waerden
had already addressed the question; in the Italian school of algebraic geometry
the ideas were well known, but foundational questions were not addressed in the same spirit.
of the (set-theoretic) intersection V ∩ W is the sum of the codimensions of V and W, respectively, i.e. the "expected" value.
Therefore the concept of moving cycles using appropriate equivalence relations on algebraic cycles is used. The equivalence must be broad enough that given any two cycles V and W, there are equivalent cycles V' and W' such that the intersection V' ∩ W' is proper. Of course, on the other hand, for a second equivalent V" and W", V' ∩ W' needs to be equivalent to V" ∩ W".
For the purposes of intersection theory, rational equivalence is the most important one. Briefly, two r-dimensional cycles on a variety X are rationally equivalent if there is a rational function f on a (k+1)-dimensional subvariety Y, i.e. an element of the function field
k(Y) or equivalently a function f : Y → P1, such that V - W = f-1(0) - f-1(∞), where f-1(-) is counted with multiplicities. Rational equivalence accomplishes the needs sketched above.
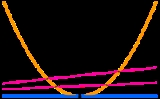
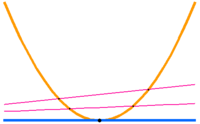The guiding principle in the definition of intersection multiplicities of cycles is continuity in a certain sense. Consider the following elementary example: the intersection of a parabola y = x2 and an axis y=0 should be 2·(0,0), because if one of the cycles moves (yet in an undefined sense), there are precisely two intersection points which both converge to (0,0) when the cycles approach the depicted position. (The picture is misleading insofar as the apparently empty intersection of the parabola and the line y=-3 is empty, because only the real solutions of the equations are depicted).
The first fully satisfactory definition of intersection multiplicities was given by Serre
: Let the ambient variety X be smooth (or all local rings regular
). Further let V and W be two (irreducible reduced closed) subvarieties, such that their intersection is proper. The construction is local, therefore the varieties may be represented by two ideals I and J in the coordinate ring of X. Let Z be an irreducible component of the set-theoretic intersection V ∩ W and z its generic point
. The multiplicity of Z in the intersection product V · W is defined by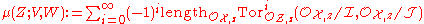
,
the alternating sum over the length
over the local ring of X in z of torsion
groups of the factor rings corresponding to the subvarieties. This expression is sometimes referred to as Serre's Tor-formula.
Remarks:
is the group of algebraic cycles modulo rational equivalence together with the following commutative intersection product: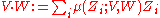
where V ∩ W = ∪︀ Zi is the decomposition of the set-theoretic intersection into irreducible components.
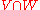, but it is also possible, though more subtle, to define the self-intersection of a single subvariety.
Given, for instance, a curve C on a surface S, its intersection with itself (as sets) is just itself:
. This is clearly correct, but on the other hand unsatisfactory: given any two distinct curves on a surface (with no component in common), they intersect in some set of points, which for instance one can count, obtaining an intersection number, and we may wish to do the same for a given curve: the analogy is that intersecting distinct curves is like multiplying two numbers: 
, while self-intersection is like squaring a single number: 
. Formally, the analogy is stated as a symmetric bilinear form
(multiplication) and a quadratic form
(squaring).
A geometric solution to this is to intersect the curve C, not with itself, but with a slightly pushed off version of itself. In the plane, this just means translating the curve C in some direction, but in general one talks about taking a curve
that is linearly equivalent
to C, and counting the intersection
, thus obtaining an intersection number, denoted 
. Note that unlike for distinct curves C and D, the actual points of intersection are not defined, because they depend on a choice of 
, but the “self intersection points of C” can be interpreted as k generic point
s on C, where
. More properly, the self-intersection points of C is the generic point of C, taken with multiplicity 
.
Alternatively, one can “solve” (or motivate) this problem algebraically by dualizing, and looking at the class of the
– this both gives a number, and raises the question of a geometric interpretation. Note that passing to cohomology classes is analogous to replacing a curve by a linear system.
Note that self-intersection number can be negative, as the example below illustrates.
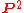: it has self-intersection number 1 since all other lines cross it once: one can push L off to 
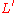, and 
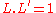(for any choice) of 
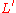, hence 
. In terms of intersection forms, we say the plane has one of type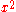 
(there is only one class of lines, and they all intersect with each other).
Note that on the affine plane, one might push off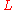
to a parallel line, so (thinking geometrically) the number of intersection points depends on the choice of push-off. One says that “the affine plane does not have a good intersection theory”, and intersection theory on non-projective varieties is much more difficult.
A line on a
(which can also be interpreted as the non-singular quadric
Q in P3) has self-intersection 0, since a line can be moved off itself. (It is a ruled surface
.) In terms of intersection forms, we say
has one of type 
(which can also be stated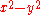 
under a change of basis
) – there are two basic classes of lines, which intersect each other in one point (
), but have zero self-intersection (no 
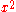or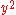 
terms).
.
Given an algebraic surface
S, blowing up
at a point creates a curve C. This curve C is recognisable by its genus, which is 0, and its self-intersection number, which is −1. (This is not obvious.)
Note that as a corollary,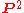
and 
are minimal surfaces
(they are not blow-ups), since they do not have any curves with negative self-intersection.
In fact, Castelnuovo
’s contraction theorem states the converse: every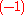
-curve is the exceptional curve of some blow-up (it can be “blown down”).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, intersection theory is a branch of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, where subvarieties are intersected on an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, and of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, where intersections are computed within the cohomology ring
Cohomology ring
In mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
. The theory for varieties is older, with roots in Bézout's theorem
Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
on curves and elimination theory
Elimination theory
In commutative algebra and algebraic geometry, elimination theory is the classical name for algorithmic approaches to eliminating between polynomials of several variables....
. On the other hand the topological theory more quickly reached a definitive form.
Topological intersection form
For a connected oriented manifoldOrientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
M of dimension 2n the intersection form is defined on the nth cohomology group (what is usually called the 'middle dimension') by the evaluation of the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
on the fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
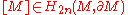. Stated precisely, there is a bilinear form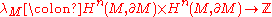given by
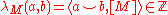
with
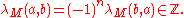
This is a symmetric form for n even, in which case the signature
Signature (topology)
In the mathematical field of topology, the signature is an integer invariant which is defined for an oriented manifold M of dimension d=4k divisible by four ....
of M is defined to be the signature of the form,
and an alternating form for n odd. It is possible to drop the orientability condition and work with
coefficients instead.These forms are important topological invariants. For example, a theorem of Michael Freedman
Michael Freedman
Michael Hartley Freedman is a mathematician at Microsoft Station Q, a research group at the University of California, Santa Barbara. In 1986, he was awarded a Fields Medal for his work on the Poincaré conjecture. Freedman and Robion Kirby showed that an exotic R4 manifold exists.Freedman was born...
states that simply connected compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
4-manifold
4-manifold
In mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
s are (almost) determined by their intersection forms up to homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
.
By Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
, it turns out that there is a way to think of this geometrically. If possible, choose representative n-dimensional submanifolds A, B for the Poincaré duals of a and b. Then
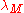(a, b) is the oriented intersection number of A and B, which is well-defined because of the dimensions of A and B. This explains the terminology intersection form.Intersection theory in algebraic geometry
William Fulton in Intersection Theory (1984) writes- ... if A and B are subvarieties of a non-singular variety X, the intersection product A.B should be an equivalence class of algebraic cycles closely related to the geometry of how A∩B, A and B are situated in X. Two extreme cases have been most familiar. If the intersection is proper, i.e. dim(A∩B) = dim A + dim B − dim X, then A.B is a linear combination of the irreducible components of A∩B, with coefficients the intersection multiplicities. At the other extreme, if A = B is a non-singular subvariety, the self-intersection formula says that A.B is represented by the top Chern classChern classIn mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of the normal bundleNormal bundleIn differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
of A in X.
To give a definition, in the general case, of the intersection multiplicity was the major concern of André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
's 1946 book Foundations of Algebraic Geometry. Work in the 1920s of B. L. van der Waerden
Bartel Leendert van der Waerden
Bartel Leendert van der Waerden was a Dutch mathematician and historian of mathematics....
had already addressed the question; in the Italian school of algebraic geometry
Italian school of algebraic geometry
In relation with the history of mathematics, the Italian school of algebraic geometry refers to the work over half a century or more done internationally in birational geometry, particularly on algebraic surfaces. There were in the region of 30 to 40 leading mathematicians who made major...
the ideas were well known, but foundational questions were not addressed in the same spirit.
Moving cycles
A well-working machinery of intersecting algebraic cycles V and W requires more than taking just the set-theoretic intersection of the cycles in question. Certainly, the intersection V ∩ W or, more commonly called intersection product, denoted V · W, should consist of the set-theoretic intersection of the two subvarieties. However it occurs that cycles are in bad position, e.g. two parallel lines in the plane, or a plane containing a line (intersecting in 3-space). In both cases the intersection should be a point, because, again, if one cycle is moved, this would be the intersection. The intersection of two cycles V and W is called proper if the codimensionCodimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
of the (set-theoretic) intersection V ∩ W is the sum of the codimensions of V and W, respectively, i.e. the "expected" value.
Therefore the concept of moving cycles using appropriate equivalence relations on algebraic cycles is used. The equivalence must be broad enough that given any two cycles V and W, there are equivalent cycles V' and W' such that the intersection V' ∩ W' is proper. Of course, on the other hand, for a second equivalent V" and W", V' ∩ W' needs to be equivalent to V" ∩ W".
For the purposes of intersection theory, rational equivalence is the most important one. Briefly, two r-dimensional cycles on a variety X are rationally equivalent if there is a rational function f on a (k+1)-dimensional subvariety Y, i.e. an element of the function field
Function field
Function field may refer to:*Function field of an algebraic variety*Function field...
k(Y) or equivalently a function f : Y → P1, such that V - W = f-1(0) - f-1(∞), where f-1(-) is counted with multiplicities. Rational equivalence accomplishes the needs sketched above.
Intersection multiplicities
The first fully satisfactory definition of intersection multiplicities was given by Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
: Let the ambient variety X be smooth (or all local rings regular
Regular local ring
In commutative algebra, a regular local ring is a Noetherian local ring having the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of...
). Further let V and W be two (irreducible reduced closed) subvarieties, such that their intersection is proper. The construction is local, therefore the varieties may be represented by two ideals I and J in the coordinate ring of X. Let Z be an irreducible component of the set-theoretic intersection V ∩ W and z its generic point
Generic point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
. The multiplicity of Z in the intersection product V · W is defined by
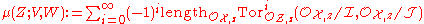,the alternating sum over the length
Length of a module
In abstract algebra, the length of a module is a measure of the module's "size". It is defined to be the length of the longest chain of submodules and is a generalization of the concept of dimension for vector spaces...
over the local ring of X in z of torsion
Tor functor
In homological algebra, the Tor functors are the derived functors of the tensor product functor. They were first defined in generality to express the Künneth theorem and universal coefficient theorem in algebraic topology....
groups of the factor rings corresponding to the subvarieties. This expression is sometimes referred to as Serre's Tor-formula.
Remarks:
- The first summand, the length of
is the "naive" guess of the multiplicity; however, as Serre shows, it is not sufficient. - The sum is finite, because the regular local ring
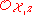has finite Tor-dimension. - If the intersection of V and W is not proper, the above multiplicity will be zero. If it is proper, it is strictly positive. (Both statements are not obvious from the definition).
- Using a spectral sequenceSpectral sequenceIn homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
argument, it can be shown that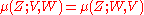
.
The Chow ring
The Chow ringChow ring
In algebraic geometry, the Chow ring of an algebraic variety is an algebraic-geometric analogue of the cohomology ring of the variety considered as a topological space: its elements are formed out of actual subvarieties and its multiplicative structure is derived from the intersection of...
is the group of algebraic cycles modulo rational equivalence together with the following commutative intersection product:
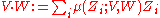
where V ∩ W = ∪︀ Zi is the decomposition of the set-theoretic intersection into irreducible components.
Self-intersection
Given two subvarieties V and W, one can take their intersection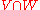, but it is also possible, though more subtle, to define the self-intersection of a single subvariety.Given, for instance, a curve C on a surface S, its intersection with itself (as sets) is just itself:
. This is clearly correct, but on the other hand unsatisfactory: given any two distinct curves on a surface (with no component in common), they intersect in some set of points, which for instance one can count, obtaining an intersection number, and we may wish to do the same for a given curve: the analogy is that intersecting distinct curves is like multiplying two numbers: , while self-intersection is like squaring a single number: . Formally, the analogy is stated as a symmetric bilinear formSymmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
(multiplication) and a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
(squaring).
A geometric solution to this is to intersect the curve C, not with itself, but with a slightly pushed off version of itself. In the plane, this just means translating the curve C in some direction, but in general one talks about taking a curve
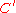that is linearly equivalentLinear system of divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family....
to C, and counting the intersection
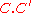, thus obtaining an intersection number, denoted . Note that unlike for distinct curves C and D, the actual points of intersection are not defined, because they depend on a choice of , but the “self intersection points of C” can be interpreted as k generic pointGeneric point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
s on C, where
. More properly, the self-intersection points of C is the generic point of C, taken with multiplicity .Alternatively, one can “solve” (or motivate) this problem algebraically by dualizing, and looking at the class of the
– this both gives a number, and raises the question of a geometric interpretation. Note that passing to cohomology classes is analogous to replacing a curve by a linear system.Note that self-intersection number can be negative, as the example below illustrates.
Examples
Consider a line L in the projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
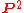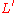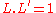: it has self-intersection number 1 since all other lines cross it once: one can push L off to , and (for any choice) of 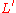, hence . In terms of intersection forms, we say the plane has one of type 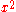(there is only one class of lines, and they all intersect with each other).Note that on the affine plane, one might push off
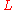to a parallel line, so (thinking geometrically) the number of intersection points depends on the choice of push-off. One says that “the affine plane does not have a good intersection theory”, and intersection theory on non-projective varieties is much more difficult.A line on a
(which can also be interpreted as the non-singular quadricQuadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
Q in P3) has self-intersection 0, since a line can be moved off itself. (It is a ruled surface
Ruled surface
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. The most familiar examples are the plane and the curved surface of a cylinder or cone...
.) In terms of intersection forms, we say
has one of type (which can also be stated 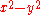under a change of basisChange of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
) – there are two basic classes of lines, which intersect each other in one point (
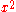), but have zero self-intersection (no or 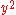terms).Blow-ups
A key example of self-intersection numbers is the exceptional curve of a blow-up, which is a central operation in birational geometryBirational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
.
Given an algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
S, blowing up
Blowing up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point...
at a point creates a curve C. This curve C is recognisable by its genus, which is 0, and its self-intersection number, which is −1. (This is not obvious.)
Note that as a corollary,
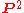and are minimal surfacesMinimal model (birational geometry)
In algebraic geometry, the minimal model program is part of the birational classification of algebraic varieties. Its goal is to construct a birational model of any complex projective variety which is as simple as possible...
(they are not blow-ups), since they do not have any curves with negative self-intersection.
In fact, Castelnuovo
Guido Castelnuovo
Guido Castelnuovo was an Italian mathematician. His father, Enrico Castelnuovo, was a novelist and campaigner for the unification of Italy...
’s contraction theorem states the converse: every
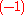-curve is the exceptional curve of some blow-up (it can be “blown down”).