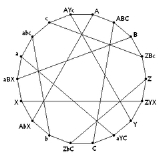
Levi graph
Encyclopedia
In combinatorial mathematics
, a Levi graph or incidence graph is a bipartite graph
associated with an incidence structure
. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for F. W. Levi, who wrote about them in 1942. The Levi graph of a system of points and lines usually has girth at least six: Any 4-cycles
would correspond to two lines through the same two points. Conversely any bipartite graph with girth at least six can be viewed as the Levi graph of an abstract incidence structure. Levi graphs may also be defined for other types of incidence structure, such as the incidences between points and planes in Euclidean space
. For every Levi graph, there is an equivalent hypergraph
, and vice versa.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, a Levi graph or incidence graph is a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
associated with an incidence structure
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for F. W. Levi, who wrote about them in 1942. The Levi graph of a system of points and lines usually has girth at least six: Any 4-cycles
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
would correspond to two lines through the same two points. Conversely any bipartite graph with girth at least six can be viewed as the Levi graph of an abstract incidence structure. Levi graphs may also be defined for other types of incidence structure, such as the incidences between points and planes in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. For every Levi graph, there is an equivalent hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
, and vice versa.
Examples
- The Desargues graphDesargues graphIn the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Gérard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial...
is the Levi graph of the Desargues configuration, composed of 10 points and 10 lines. There are 3 points on each line, and 3 lines passing through each point. The Desargues graph can also be viewed as the generalized Petersen graphGeneralized Petersen graphIn graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized...
G(10,3) or the bipartite Kneser graphKneser graphIn graph theory, the Kneser graph is the graph whose vertices correspond to the -element subsets of a set of elements, and where two vertices are connected if and only if the two corresponding sets are disjoint...
with parameters 5,2. It is 3-regular with 20 vertices.
- The Heawood graphHeawood graphIn the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.-Combinatorial properties:...
is the Levi graph of the Fano planeFano planeIn finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
. It is also known as the (3,6)-cageCage (graph theory)In the mathematical area of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.Formally, an -graph is defined to be a graph in which each vertex has exactly r neighbors, and in which the shortest cycle has length exactly g. It is known that an -graph exists...
, and is 3-regular with 14 vertices.
- The Möbius–Kantor graphMöbius–Kantor graphIn the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor...
is the Levi graph of the Möbius–Kantor configuration, a system of 8 points and 8 lines that cannot be realized by straight lines in the Euclidean plane. It is 3-regular with 16 vertices.
- The Pappus graphPappus graphIn the mathematical field of graph theory, the Pappus graph is a 3-regular undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon...
is the Levi graph of the Pappus configuration, composed of 9 points and 9 lines. Like the Desargues configuration there are 3 points on each line and 3 lines passing through each point. It is 3-regular with 18 vertices.
- The Gray graphGray graphIn the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 , then discovered independently by Bouwer 1968 in reply to a question...
is the Levi graph of a configuration that can be realized in R3 as a 3×3×3 grid of 27 points and the 27 orthogonal lines through them.
- The Tutte eight-cageTutte eight-cageIn the mathematical field of graph theory, the Tutte–Coxeter graph or Tutte eight-cage is a 3-regular graph with 30 vertices and 45 edges. As the unique smallest cubic graph of girth 8 it is a cage and a Moore graph. It is bipartite, and can be constructed as the Levi graph of the generalized...
is the Levi graph of the Cremona–Richmond configuration. It is also known as the (3,8)-cage, and is 3-regular with 30 vertices.
- The four-dimensional hypercube graph Q4 is the Levi graph of the Möbius configurationMöbius configurationIn geometry, the Möbius configuration is a certain configuration in Euclidean space consisting of two mutually inscribed tetrahedra: each vertex of one tetrahedron lies on a face plane of the other tetrahedron and vice versa...
formed by the points and planes of two mutually incident tetrahedra.
- The Ljubljana graphLjubljana graphIn the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges.It is a cubic graph with diameter 8, radius 7, chromatic number 2 and chromatic index 3. Its girth is 10 and there are exactly 168 cycles of length 10 in it...
on 112 vertices is the Levi graph of the Ljubljana configuration.

