
Ideal lattice cryptography
Encyclopedia
Ideal lattices are a special class of lattices and a generalization of cyclic lattices. Ideal lattices naturally occur in many parts of number theory
, but also in other areas. In particular, they have a significant place in cryptography
. Micciancio defined a generalization of cyclic lattices as ideal lattices. They can be used in cryptosystems to decrease by a square root the number of parameters necessary to describe a lattice, making them more efficient. Ideal lattices are a new concept, but similar lattice classes have been used for a long time. For example cyclic lattices, a special case of ideal lattices, are used in NTRUEncrypt
and NTRUSign
.
in rings
of the form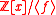 for some irreducible polynomial
for some irreducible polynomial
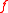 of degree
of degree  . All of the definitions of ideal lattices from prior work are instances of the following general notion: let
. All of the definitions of ideal lattices from prior work are instances of the following general notion: let  be a ring
be a ring
whose additive group
is isomorphic
to (i.e., it is a free
(i.e., it is a free  -module of rank
-module of rank  ), and let
), and let  be an additive isomorphism
be an additive isomorphism
mapping to some lattice
to some lattice 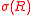 in an
in an  -dimensional real vector space
-dimensional real vector space
(e.g.,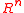 ). The family of ideal lattices for the ring
). The family of ideal lattices for the ring  under the embedding
under the embedding  is the set of all lattices
is the set of all lattices  , where
, where  is an ideal
is an ideal
in
 be a monic polynomial of degree
be a monic polynomial of degree  , and consider the quotient ring
, and consider the quotient ring
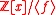 .
.
Using the standard set of representatives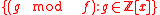 , and identification of polynomials with vectors, the quotient ring
, and identification of polynomials with vectors, the quotient ring
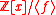 is isomorphic
is isomorphic
(as an additive group
) to the integer lattice
 , and any ideal
, and any ideal
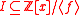 defines a corresponding integer sublattice
defines a corresponding integer sublattice 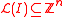 .
.
An ideal lattice is an integer lattice
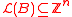 such that
such that  for some monic polynomial
for some monic polynomial 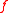 of degree
of degree  and ideal
and ideal
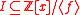 .
.
 for the resulting function to be collision resistant are:
for the resulting function to be collision resistant are:
The first property implies that every ideal of the ring
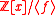 defines a full-rank lattice in
defines a full-rank lattice in 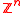 and plays a fundamental role in proofs.
and plays a fundamental role in proofs.
Lemma: Every ideal
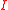 of
of 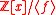 , where
, where  is a monic, irreducible
is a monic, irreducible
integer polynomial of degree , is isomorphic to a full-rank lattice in
, is isomorphic to a full-rank lattice in 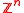 .
.
Ding and Lindner gave evidence that distinguishing ideal lattices from general ones can be done in polynomial time and showed that in practice randomly chosen lattices are never ideal. They only considered the case where the lattice has full rank, i.e. the basis consists of linear independent vectors
linear independent vectors
. This is not a fundamental restriction because Lyubashevsky and Micciancio have shown that if a lattice is ideal with respect to an irreducible monic polynomial, then it has full rank, as given in the above lemma.
Algorithm: Identifying ideal lattices with full rank bases
Data: A full-rank basis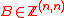
Result: true and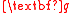 , if
, if  spans an ideal lattice with respect to
spans an ideal lattice with respect to  , otherwise false.
, otherwise false.
where the matrix M is
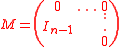
Using this algorithm, it can be seen that many lattices are not ideal lattices. For example let and
and 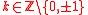 , then
, then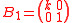
is ideal, but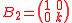
is not.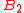 with
with  is an example given by Lyubashevsky and Micciancio.
is an example given by Lyubashevsky and Micciancio.
Performing the algorithm on it and referring to the basis as B, matrix B is already in Hermite Normal Form
so the first step is not needed. The determinant is , the adjugate matrix
, the adjugate matrix
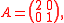
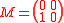
and finally, the product is
is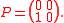
At this point the algorithm stops, because all but the last column of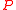 have to be zero if
have to be zero if  would span an ideal lattice.
would span an ideal lattice.
s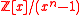 , and presented the first provably secure one-way function based on the worst-case hardness
, and presented the first provably secure one-way function based on the worst-case hardness
of the restriction of Poly(n)-SVP to cyclic lattices. (The problem γ-SVP consists in computing a non-zero vector of a given lattice, whose norm is no more than γ times larger than the norm of a shortest non-zero lattice vector.) At the same time, thanks to its algebraic structure, this one-way function enjoys high efficiency comparable to the NTRU
scheme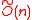 evaluation time and storage cost). Subsequently, Lyubashevsky and Micciancio and independently Peikert and Rosen showed how to modify Micciancio’s function to construct an efficient and provably secure collision resistant
evaluation time and storage cost). Subsequently, Lyubashevsky and Micciancio and independently Peikert and Rosen showed how to modify Micciancio’s function to construct an efficient and provably secure collision resistant
hash function
. For this, they introduced the more general class of ideal lattices, which correspond to ideals
in polynomial ring
s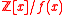 . The collision resistance
. The collision resistance
relies on the hardness of the restriction of Poly(n)-SVP to ideal lattices (called Poly(n)-Ideal-SVP). The average-case collision-finding problem is a natural computational problem called Ideal-SIS, which has been shown to be as hard as the worst-case instances of Ideal-SVP. Provably secure efficient signature schemes from ideal lattices have also been proposed, but constructing efficient provably secure public key encryption
from ideal lattices was an interesting open problem
.
stems from the fact that very efficient and practical collision resistant
hash functions
can be built based on the hardness of finding an approximate shortest vector in such lattices.
Independently constructed collision resistant
hash functions
by Peikert and Rosen, and Lyubashevsky and Micciancio based on ideal lattices (a generalization of cyclic lattices), and provided a fast and practical implementation. These results paved the way for other efficient cryptographic constructions including identification schemes and signatures.
Lyubashevsky and Micciancio gave constructions of efficient collision resistant
hash functions
that can be proven secure based on worst case hardness of the shortest vector problem for ideal lattices. They defined hash function
families as: Given a ring
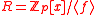 , where
, where 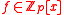 is a monic, irreducible polynomial
is a monic, irreducible polynomial
of degree and
and 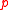 is an integer of order roughly
is an integer of order roughly 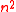 , generate
, generate  random elements
random elements 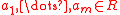 , where
, where  is a constant. The ordered
is a constant. The ordered  -tuple
-tuple  determines the hash function. It will map elements in
determines the hash function. It will map elements in 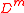 , where
, where  is a strategically chosen subset of
is a strategically chosen subset of  , to
, to  . For an element
. For an element 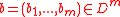 , the hash is
, the hash is 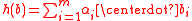 . Here the size of the key (the hash function
. Here the size of the key (the hash function
) is , and the operation
, and the operation  can be done in time
can be done in time 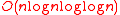 by using the Fast Fourier Transform (FFT)
by using the Fast Fourier Transform (FFT)
, for appropriate choice of the polynomial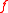 . Since
. Since  is a constant,
is a constant,
hashing requires time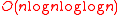 . They proved that the hash function
. They proved that the hash function
family is collision resistant
by showing that there is a polynomial-time algorithm that succeeds with non-negligible probability in finding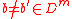 such that
such that
 , for a randomly chosen hash function
, for a randomly chosen hash function
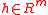 , then a certain
, then a certain
problem called the “shortest vector problem” is solvable in polynomial time for every ideal
of the ring
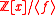 .
.
Based on the work of Lyubashevsky and Micciancio in 2006, Micciancio and Regev defined the following algorithm of hash functions
based on ideal lattices:
Here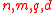 are parameters, f is a vector in
are parameters, f is a vector in 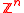 and
and  is a block-matrix with structured blocks
is a block-matrix with structured blocks 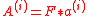 .
.
Finding short vectors in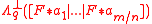 on the average (even with just inverse polynomial
on the average (even with just inverse polynomial
probability) is as hard as solving various lattice problems (such as approximate SVP and SIVP) in the worst
case over ideal lattices, provided the vector f satisfies the following two properties:
The first property is satisfied by the vector f =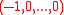 corresponding to circulant matrices
corresponding to circulant matrices
,
because all the coordinates of [F∗u]v are bounded by 1, and hence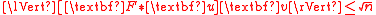 . However, the polynomial
. However, the polynomial  corresponding to f =
corresponding to f = 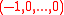 is not irreducible
is not irreducible
because it factors into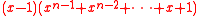 , and this is why collisions can be efficiently found. So, f =
, and this is why collisions can be efficiently found. So, f =  is not a good choice to get collision resistant
is not a good choice to get collision resistant
hash functions
, but many other choices are possible. For example, some choices of f for which both properties are satisfied (and therefore, result in collision resistant
hash functions
with worst-case security guarantees) are
s schemes are among the most important cryptographic primitives. They can be obtained by using the one-way functions based on the worst-case hardness
of lattice problems. However, they are impractical. The most recent efficient scheme was provided by Lyubashevsky and Micciancio.
Their direct construction of digital signature
s based on the complexity of approximating the shortest vector in ideal (e.g., cyclic) lattices. The scheme of Lyubashevsky and Micciancio has worst-case security guarantees based on ideal lattices and it is the most asymptotically efficient construction known to date, yielding signature generation and verification algorithms that run in almost linear time.
One of the main open problems that was raised by their work is constructing a one-time signature with similar efficiency, but based on a weaker hardness
assumption. For instance, it would be great to provide a one-time signature with security based on the hardness
of approximating the Shortest Vector Problem (SVP) (in ideal lattices) to within a factor of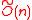 .
.
Their construction is based on a standard transformation from one-time signatures (i.e. signatures that allow to securely sign a single message) to general signature schemes, together with a novel construction of a lattice based one-time signature whose security is ultimately based on the worst-case hardness
of approximating the shortest vector in all lattices corresponding to ideals
in the ring
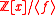 for any irreducible polynomial
for any irreducible polynomial
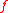 .
.
Key-Generation Algorithm:
Input: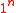 , irreducible polynomial
, irreducible polynomial
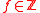 of degree
of degree  .
.
Signing Algorithm:
Input: Message such that
such that 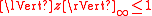 ; signing key
; signing key 
Output: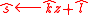
Verification Algorithm:
Input: Message ; signature
; signature  ; verification key
; verification key 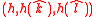
Output: “ACCEPT”, if and
and 
“REJECT”, otherwise.
is quite efficient and can be computed asymptotically in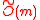 time using the Fast Fourier Transform (FFT)
time using the Fast Fourier Transform (FFT)
over the complex number
s. However, in practice, this carries a substantial overhead. The SWIFFT
family of hash functions
defined by Micciancio and Regev is essentially a highly optimized variant of the hash function
avobe using the (FFT)
in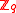 . The vector f is set to
. The vector f is set to 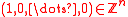 for
for  equal to a power of 2, so that the corresponding polynomial
equal to a power of 2, so that the corresponding polynomial  is irreducible
is irreducible
.
Let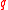 be a prime number
be a prime number
such that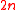 divides
divides 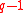 , and let
, and let  be an invertible matrix over
be an invertible matrix over 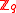 to be chosen later. The SWIFFT
to be chosen later. The SWIFFT
hash function
maps a key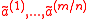 consisting of
consisting of 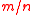 vectors chosen uniformly from
vectors chosen uniformly from 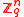 and an input
and an input  to
to 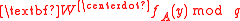 where
where 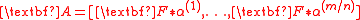 is as before and
is as before and  .
.
Multiplication by the invertible matrix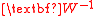 maps a uniformly chosen
maps a uniformly chosen 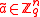 to a uniformly chosen
to a uniformly chosen 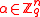 . Moreover,
. Moreover,  if and only if
if and only if 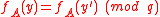 .
.
Together, these two facts establish that finding collisions in SWIFFT
is equivalent to finding collisions in the underlying ideal lattice function , and the claimed collision resistance
, and the claimed collision resistance
property of SWIFFT
is supported by the connection to worst case lattice problems on ideal lattices.
The algorithm of the SWIFFT hash function is:
problem has been shown to be as hard as worst-case lattice problems and has served as the foundation for plenty of cryptographic applications. However, these applications are inefficient because of an inherent quadratic overhead in the use of LWE
. To get truly efficient LWE
applications, Lyubashevsky, Peikert and Regev defined an appropriate version of the LWE
problem in a wide class of rings and proved its hardness under worst-case assumptions on ideal lattices in these rings. They called their LWE
version ring-LWE.
Let , where the security parameter
, where the security parameter  is a power of 2, making
is a power of 2, making 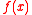 irreducible over the rationals. (This particular
irreducible over the rationals. (This particular 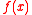 comes from the family of cyclotomic polynomial
comes from the family of cyclotomic polynomial
s, which play a special role in this work).
Let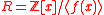 be the ring of integer polynomials modulo
be the ring of integer polynomials modulo  . Elements of
. Elements of  (i.e., residues modulo
(i.e., residues modulo 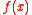 ) are typically represented by integer polynomials of degree less than
) are typically represented by integer polynomials of degree less than  . Let
. Let  be a sufficiently large public prime modulus (bounded by a polynomial in
be a sufficiently large public prime modulus (bounded by a polynomial in  ), and let
), and let 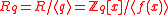 be the ring of integer polynomials modulo both
be the ring of integer polynomials modulo both 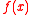 and
and 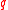 . Elements of
. Elements of 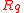 may be represented by polynomials of degree less than
may be represented by polynomials of degree less than  -whose coefficients are from
-whose coefficients are from 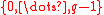 .
.
In the above-described ring, the R-LWE problem may be described as follows.
Let be a uniformly random ring element, which is kept secret. Analogously to standard LWE, the goal of the attacker is to distinguish arbitrarily many (independent) ‘random noisy ring equations’ from truly uniform ones. More specifically, the noisy equations are of the form
be a uniformly random ring element, which is kept secret. Analogously to standard LWE, the goal of the attacker is to distinguish arbitrarily many (independent) ‘random noisy ring equations’ from truly uniform ones. More specifically, the noisy equations are of the form 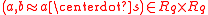 , where a is uniformly random and the product
, where a is uniformly random and the product  is perturbed by some ‘small’ random error term, chosen from a certain distribution over
is perturbed by some ‘small’ random error term, chosen from a certain distribution over  .
.
They gave a quantum reduction from approximate SVP (in the worst case) on ideal lattices in to the search version of ring-LWE, where the goal is to recover the secret
to the search version of ring-LWE, where the goal is to recover the secret 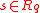 (with high probability, for any
(with high probability, for any  ) from arbitrarily many noisy products. This result follows the general outline of Regev’s iterative quantum reduction for general lattices, but ideal lattices introduce several new technical roadblocks in both the ‘algebraic’ and ‘geometric’ components of the reduction. They used algebraic number theory, in particular, the canonical embedding of a number field and the Chinese Remainder Theorem
) from arbitrarily many noisy products. This result follows the general outline of Regev’s iterative quantum reduction for general lattices, but ideal lattices introduce several new technical roadblocks in both the ‘algebraic’ and ‘geometric’ components of the reduction. They used algebraic number theory, in particular, the canonical embedding of a number field and the Chinese Remainder Theorem
to overcome these obstacles. They got the following theorem:
Theorem Let be an arbitrary number field of degree
be an arbitrary number field of degree  . Let
. Let 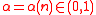 be arbitrary, and let the (rational) integer modulus
be arbitrary, and let the (rational) integer modulus 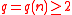 be such that
be such that 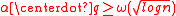 . There is a probabilistic polynomial-time quantum reduction from
. There is a probabilistic polynomial-time quantum reduction from  -
-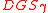 to
to 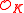 -
- 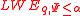 , where
, where  .
.
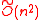 -Ideal-SVP against subexponential quantum attacks. It achieves asymptotically optimal efficiency: the public/private key length is
-Ideal-SVP against subexponential quantum attacks. It achieves asymptotically optimal efficiency: the public/private key length is 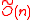 bits and the amortized encryption/decryption cost is
bits and the amortized encryption/decryption cost is  bit operations per message bit (encrypting
bit operations per message bit (encrypting 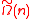 bits at once, at a
bits at once, at a 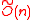 cost). The security assumption here is that
cost). The security assumption here is that 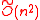 -Ideal-SVP cannot be solved by any subexponential time quantum algorithm. It is noteworthy that this is stronger than standard public key cryptography
-Ideal-SVP cannot be solved by any subexponential time quantum algorithm. It is noteworthy that this is stronger than standard public key cryptography
security assumptions. On the other hand, contrary to the most of public key cryptography
, lattice-based cryptography allows security against subexponential quantum attacks.
Most of the cryptosystems based on general lattices rely on the average-case hardness of the Learning with errors (LWE)
. Their scheme is based on a structured variant of LWE, that they call Ideal-LWE. They needed to introduce some techniques to circumvent two main difficulties that arise from the restriction to ideal lattices. Firstly, the previous cryptosystems based on unstructured lattices all make use of Regev’s worst-case to average-case classical reduction from Bounded Distance Deconding problem (BDD) to LWE
(this is the classical step in the quantum reduction from SVP to LWE
). This reduction exploits the unstructured-ness of the considered lattices, and does not seem to carry over to the structured lattices involved in Ideal-LWE. In particular, the probabilistic independence of the rows of the LWE matrices allows to consider a single row. Secondly, the other ingredient used in previous cryptosystems, namely Regev’s reduction from the computational variant of LWE
to its decisional variant, also seems to fail for Ideal-LWE: it relies on the probabilistic independence of the columns of the LWE
matrices.
To overcome these difficulties, they avoided the classical step of the reduction. Instead, they used the quantum step to construct a new quantum average-case reduction from SIS (average-case collision-finding problem) to LWE
. It also works from Ideal-SIS to Ideal-LWE. Combined with the reduction from worst-case Ideal-SVP to average-case Ideal-SIS, they obtained the a quantum reduction from Ideal-SVP to Ideal-LWE. This shows the hardness of the computational variant of Ideal-LWE. Because they did not obtain the hardness of the decisional variant, they used a generic hardcore function to derive pseudorandom bits for encryption. This is why they needed to assume the exponential hardness of SVP.
 is homomorphic for circuits in
is homomorphic for circuits in 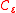 if
if  is correct for
is correct for  and
and  can be expressed as a circuit
can be expressed as a circuit 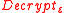 of size
of size 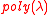 .
.  is fully homomorphic if it is homomorphic for all circuits. A fully homomorphic encryption
is fully homomorphic if it is homomorphic for all circuits. A fully homomorphic encryption
scheme is the one which allows one to evaluate circuits over encrypted data without being able to decrypt. Gentry proposed a solution to the problem of constructing a fully homomorphic encryption
scheme, which was introduced by Rivest, Adleman and Dertouzos shortly after the invention of RSA by Rivest, Adleman and Shamir in 1978. His scheme was based on ideal lattices.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, but also in other areas. In particular, they have a significant place in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
. Micciancio defined a generalization of cyclic lattices as ideal lattices. They can be used in cryptosystems to decrease by a square root the number of parameters necessary to describe a lattice, making them more efficient. Ideal lattices are a new concept, but similar lattice classes have been used for a long time. For example cyclic lattices, a special case of ideal lattices, are used in NTRUEncrypt
NTRUEncrypt
The NTRUEncrypt public key cryptosystem, also known as the NTRU encryption algorithm, is a lattice-based alternative to RSA and ECC and is based on the shortest vector problem in a lattice...
and NTRUSign
NTRUSign
NTRUSign, also known as the NTRU Signature Algorithm, is a public key cryptography digital signature algorithm based on the GGH signature scheme. It was first presented at the rump session of Asiacrypt 2001 and published in peer-reviewed form at the RSA Conference 2003. The 2003 publication...
.
Introduction
In general terms, ideal lattices are lattices corresponding to idealsIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of the form
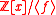 for some irreducible polynomial
for some irreducible polynomialIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
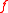 of degree
of degree  . All of the definitions of ideal lattices from prior work are instances of the following general notion: let
. All of the definitions of ideal lattices from prior work are instances of the following general notion: let  be a ring
be a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
whose additive group
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to
 (i.e., it is a free
(i.e., it is a free  -module of rank
-module of rank  ), and let
), and let  be an additive isomorphism
be an additive isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
mapping
 to some lattice
to some lattice 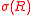 in an
in an  -dimensional real vector space
-dimensional real vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
(e.g.,
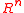 ). The family of ideal lattices for the ring
). The family of ideal lattices for the ring  under the embedding
under the embedding  is the set of all lattices
is the set of all lattices  , where
, where  is an ideal
is an idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in

Notation
Let be a monic polynomial of degree
be a monic polynomial of degree  , and consider the quotient ring
, and consider the quotient ringQuotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
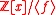 .
.Using the standard set of representatives
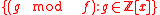 , and identification of polynomials with vectors, the quotient ring
, and identification of polynomials with vectors, the quotient ringQuotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
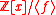 is isomorphic
is isomorphicGroup isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
(as an additive group
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
) to the integer lattice
Integer lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
 , and any ideal
, and any idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
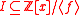 defines a corresponding integer sublattice
defines a corresponding integer sublattice 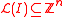 .
.An ideal lattice is an integer lattice
Integer lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
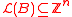 such that
such that  for some monic polynomial
for some monic polynomial 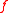 of degree
of degree  and ideal
and idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
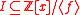 .
.Related properties
It turns out that the relevant properties of for the resulting function to be collision resistant are:
for the resulting function to be collision resistant are:
-
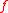 should be irreducibleIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
should be irreducibleIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
. - the ring norm
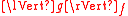 is not much bigger than
is not much bigger than 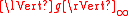 for any polynomial
for any polynomial 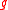 , in a quantitative sense.
, in a quantitative sense.
The first property implies that every ideal of the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
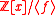 defines a full-rank lattice in
defines a full-rank lattice in 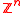 and plays a fundamental role in proofs.
and plays a fundamental role in proofs.Lemma: Every ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
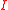 of
of 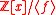 , where
, where  is a monic, irreducible
is a monic, irreducibleIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
integer polynomial of degree
 , is isomorphic to a full-rank lattice in
, is isomorphic to a full-rank lattice in 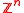 .
.Ding and Lindner gave evidence that distinguishing ideal lattices from general ones can be done in polynomial time and showed that in practice randomly chosen lattices are never ideal. They only considered the case where the lattice has full rank, i.e. the basis consists of
 linear independent vectors
linear independent vectorsLinear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
. This is not a fundamental restriction because Lyubashevsky and Micciancio have shown that if a lattice is ideal with respect to an irreducible monic polynomial, then it has full rank, as given in the above lemma.
Algorithm: Identifying ideal lattices with full rank bases
Data: A full-rank basis
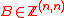
Result: true and
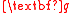 , if
, if  spans an ideal lattice with respect to
spans an ideal lattice with respect to  , otherwise false.
, otherwise false.- Transform
 into HNFHermite normal formIn linear algebra, the Hermite normal form is an analogue of reduced echelon form for matrices over the integers Z.-Nonsingular square matrices:...
into HNFHermite normal formIn linear algebra, the Hermite normal form is an analogue of reduced echelon form for matrices over the integers Z.-Nonsingular square matrices:... - Calculate
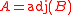 ,
, 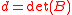 , and
, and 
- Calculate the product

- if only the last column of P is non-zero then
- set
 to equal this column
to equal this column - else return false
- if
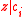 for
for 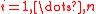 then
then - use CRTChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
to find and
and 
- else return false
- if
 then
then - return true,
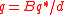
- else return false
where the matrix M is
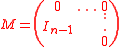
Using this algorithm, it can be seen that many lattices are not ideal lattices. For example let
 and
and 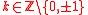 , then
, then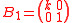
is ideal, but
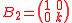
is not.
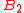 with
with  is an example given by Lyubashevsky and Micciancio.
is an example given by Lyubashevsky and Micciancio.Performing the algorithm on it and referring to the basis as B, matrix B is already in Hermite Normal Form
Hermite normal form
In linear algebra, the Hermite normal form is an analogue of reduced echelon form for matrices over the integers Z.-Nonsingular square matrices:...
so the first step is not needed. The determinant is
 , the adjugate matrix
, the adjugate matrixAdjugate matrix
In linear algebra, the adjugate or classical adjoint of a square matrix is a matrix that plays a role similar to the inverse of a matrix; it can however be defined for any square matrix without the need to perform any divisions....
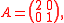
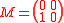
and finally, the product
 is
is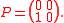
At this point the algorithm stops, because all but the last column of
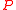 have to be zero if
have to be zero if  would span an ideal lattice.
would span an ideal lattice.Use in cryptography
Micciancio introduced the class of structured cyclic lattices, which correspond to ideals in polynomial ringPolynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
s
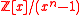 , and presented the first provably secure one-way function based on the worst-case hardness
, and presented the first provably secure one-way function based on the worst-case hardnessHardness of approximation
In computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. It complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can...
of the restriction of Poly(n)-SVP to cyclic lattices. (The problem γ-SVP consists in computing a non-zero vector of a given lattice, whose norm is no more than γ times larger than the norm of a shortest non-zero lattice vector.) At the same time, thanks to its algebraic structure, this one-way function enjoys high efficiency comparable to the NTRU
NTRUEncrypt
The NTRUEncrypt public key cryptosystem, also known as the NTRU encryption algorithm, is a lattice-based alternative to RSA and ECC and is based on the shortest vector problem in a lattice...
scheme
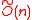 evaluation time and storage cost). Subsequently, Lyubashevsky and Micciancio and independently Peikert and Rosen showed how to modify Micciancio’s function to construct an efficient and provably secure collision resistant
evaluation time and storage cost). Subsequently, Lyubashevsky and Micciancio and independently Peikert and Rosen showed how to modify Micciancio’s function to construct an efficient and provably secure collision resistantCollision resistance
Collision resistance is a property of cryptographic hash functions: a hash function is collision resistant if it is hard to find two inputs that hash to the same output; that is, two inputs a and b such that H = H, and a ≠ b.Every hash function with more inputs than outputs will necessarily have...
hash function
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
. For this, they introduced the more general class of ideal lattices, which correspond to ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
s
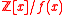 . The collision resistance
. The collision resistanceCollision resistance
Collision resistance is a property of cryptographic hash functions: a hash function is collision resistant if it is hard to find two inputs that hash to the same output; that is, two inputs a and b such that H = H, and a ≠ b.Every hash function with more inputs than outputs will necessarily have...
relies on the hardness of the restriction of Poly(n)-SVP to ideal lattices (called Poly(n)-Ideal-SVP). The average-case collision-finding problem is a natural computational problem called Ideal-SIS, which has been shown to be as hard as the worst-case instances of Ideal-SVP. Provably secure efficient signature schemes from ideal lattices have also been proposed, but constructing efficient provably secure public key encryption
Public-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
from ideal lattices was an interesting open problem
Open problem
In science and mathematics, an open problem or an open question is a known problem that can be accurately stated, and has not yet been solved . Some questions remain unanswered for centuries before solutions are found...
.
Efficient collision resistant hash functions
The main usefulness of the ideal lattices in cryptographyCryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
stems from the fact that very efficient and practical collision resistant
Collision resistance
Collision resistance is a property of cryptographic hash functions: a hash function is collision resistant if it is hard to find two inputs that hash to the same output; that is, two inputs a and b such that H = H, and a ≠ b.Every hash function with more inputs than outputs will necessarily have...
hash functions
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
can be built based on the hardness of finding an approximate shortest vector in such lattices.
Independently constructed collision resistant
Collision resistance
Collision resistance is a property of cryptographic hash functions: a hash function is collision resistant if it is hard to find two inputs that hash to the same output; that is, two inputs a and b such that H = H, and a ≠ b.Every hash function with more inputs than outputs will necessarily have...
hash functions
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
by Peikert and Rosen, and Lyubashevsky and Micciancio based on ideal lattices (a generalization of cyclic lattices), and provided a fast and practical implementation. These results paved the way for other efficient cryptographic constructions including identification schemes and signatures.
Lyubashevsky and Micciancio gave constructions of efficient collision resistant
Collision resistance
Collision resistance is a property of cryptographic hash functions: a hash function is collision resistant if it is hard to find two inputs that hash to the same output; that is, two inputs a and b such that H = H, and a ≠ b.Every hash function with more inputs than outputs will necessarily have...
hash functions
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
that can be proven secure based on worst case hardness of the shortest vector problem for ideal lattices. They defined hash function
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
families as: Given a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
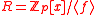 , where
, where 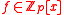 is a monic, irreducible polynomial
is a monic, irreducible polynomialIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
of degree
 and
and 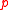 is an integer of order roughly
is an integer of order roughly 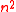 , generate
, generate  random elements
random elements 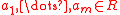 , where
, where  is a constant. The ordered
is a constant. The ordered  -tuple
-tuple  determines the hash function. It will map elements in
determines the hash function. It will map elements in 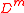 , where
, where  is a strategically chosen subset of
is a strategically chosen subset of  , to
, to  . For an element
. For an element 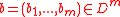 , the hash is
, the hash is 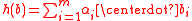 . Here the size of the key (the hash function
. Here the size of the key (the hash functionCryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
) is
 , and the operation
, and the operation  can be done in time
can be done in time 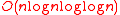 by using the Fast Fourier Transform (FFT)
by using the Fast Fourier Transform (FFT)Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
, for appropriate choice of the polynomial
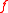 . Since
. Since  is a constant,
is a constant,hashing requires time
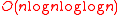 . They proved that the hash function
. They proved that the hash functionCryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
family is collision resistant
Collision resistance
Collision resistance is a property of cryptographic hash functions: a hash function is collision resistant if it is hard to find two inputs that hash to the same output; that is, two inputs a and b such that H = H, and a ≠ b.Every hash function with more inputs than outputs will necessarily have...
by showing that there is a polynomial-time algorithm that succeeds with non-negligible probability in finding
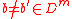 such that
such that , for a randomly chosen hash function
, for a randomly chosen hash functionCryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
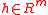 , then a certain
, then a certainproblem called the “shortest vector problem” is solvable in polynomial time for every ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
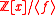 .
.Based on the work of Lyubashevsky and Micciancio in 2006, Micciancio and Regev defined the following algorithm of hash functions
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
based on ideal lattices:
- Parameters: Integers
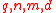 with
with 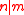 , and vector f
, and vector f 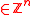 .
. - Key:
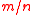 vectors
vectors 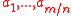 chosen independently and uniformly at random in
chosen independently and uniformly at random in 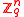 .
. - Hash function:
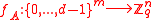 given by
given by  .
.
Here
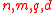 are parameters, f is a vector in
are parameters, f is a vector in 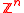 and
and  is a block-matrix with structured blocks
is a block-matrix with structured blocks 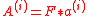 .
.Finding short vectors in
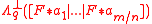 on the average (even with just inverse polynomial
on the average (even with just inverse polynomialprobability) is as hard as solving various lattice problems (such as approximate SVP and SIVP) in the worst
case over ideal lattices, provided the vector f satisfies the following two properties:
- For any two unit vectors u, v, the vector [F∗u]v has small (say, polynomial in
 , typically
, typically 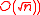 norm.
norm. - The polynomial
 is irreducibleIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
is irreducibleIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over the integers, i.e., it does not factor into the product of integer polynomials of smaller degree.
The first property is satisfied by the vector f =
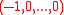 corresponding to circulant matrices
corresponding to circulant matricesCirculant matrix
In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
,
because all the coordinates of [F∗u]v are bounded by 1, and hence
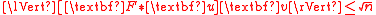 . However, the polynomial
. However, the polynomial  corresponding to f =
corresponding to f = 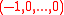 is not irreducible
is not irreducibleIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
because it factors into
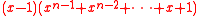 , and this is why collisions can be efficiently found. So, f =
, and this is why collisions can be efficiently found. So, f =  is not a good choice to get collision resistant
is not a good choice to get collision resistantCollision resistance
Collision resistance is a property of cryptographic hash functions: a hash function is collision resistant if it is hard to find two inputs that hash to the same output; that is, two inputs a and b such that H = H, and a ≠ b.Every hash function with more inputs than outputs will necessarily have...
hash functions
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
, but many other choices are possible. For example, some choices of f for which both properties are satisfied (and therefore, result in collision resistant
Collision resistance
Collision resistance is a property of cryptographic hash functions: a hash function is collision resistant if it is hard to find two inputs that hash to the same output; that is, two inputs a and b such that H = H, and a ≠ b.Every hash function with more inputs than outputs will necessarily have...
hash functions
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
with worst-case security guarantees) are
- f =
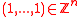 where
where  is prime, and
is prime, and - f =
 for
for  equal to a power of 2.
equal to a power of 2.
Digital signatures
Digital signatureDigital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
s schemes are among the most important cryptographic primitives. They can be obtained by using the one-way functions based on the worst-case hardness
Hardness of approximation
In computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. It complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can...
of lattice problems. However, they are impractical. The most recent efficient scheme was provided by Lyubashevsky and Micciancio.
Their direct construction of digital signature
Digital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
s based on the complexity of approximating the shortest vector in ideal (e.g., cyclic) lattices. The scheme of Lyubashevsky and Micciancio has worst-case security guarantees based on ideal lattices and it is the most asymptotically efficient construction known to date, yielding signature generation and verification algorithms that run in almost linear time.
One of the main open problems that was raised by their work is constructing a one-time signature with similar efficiency, but based on a weaker hardness
Hardness of approximation
In computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. It complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can...
assumption. For instance, it would be great to provide a one-time signature with security based on the hardness
Hardness of approximation
In computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. It complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can...
of approximating the Shortest Vector Problem (SVP) (in ideal lattices) to within a factor of
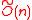 .
.Their construction is based on a standard transformation from one-time signatures (i.e. signatures that allow to securely sign a single message) to general signature schemes, together with a novel construction of a lattice based one-time signature whose security is ultimately based on the worst-case hardness
Hardness of approximation
In computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. It complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can...
of approximating the shortest vector in all lattices corresponding to ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
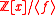 for any irreducible polynomial
for any irreducible polynomialIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
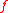 .
.Key-Generation Algorithm:
Input:
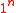 , irreducible polynomial
, irreducible polynomialIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
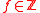 of degree
of degree  .
.
- Set
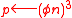 ,
, 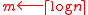 ,
, 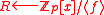
- For all positive
 , let the sets
, let the sets 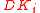 and
and 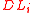 be defined as:
be defined as: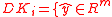 such that
such that 
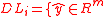 such that
such that 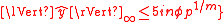
- Choose uniformly random
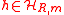
- Pick a uniformly random string
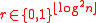
- If
 then
then - Set
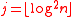
- else
- Set
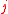 to the position of the first 1 in the string
to the position of the first 1 in the string 
- end if
- Pick
 independently and uniformly at random from
independently and uniformly at random from 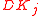 and
and 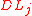 respectively
respectively - Signing Key:
 . Verification Key:
. Verification Key: 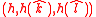
Signing Algorithm:
Input: Message
 such that
such that 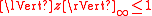 ; signing key
; signing key 
Output:
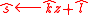
Verification Algorithm:
Input: Message
 ; signature
; signature  ; verification key
; verification key 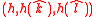
Output: “ACCEPT”, if
 and
and 
“REJECT”, otherwise.
The SWIFFT hash function
The hash functionCryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
is quite efficient and can be computed asymptotically in
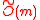 time using the Fast Fourier Transform (FFT)
time using the Fast Fourier Transform (FFT)Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. However, in practice, this carries a substantial overhead. The SWIFFT
SWIFFT
In cryptography, SWIFFT is a collection of provably secure hash functions. It is based on the concept of the Fast Fourier Transform . SWIFFT is not the first hash function based on FFT, but it sets itself apart by providing a mathematical proof of its security. It also uses the LLL basis reduction...
family of hash functions
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
defined by Micciancio and Regev is essentially a highly optimized variant of the hash function
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
avobe using the (FFT)
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
in
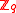 . The vector f is set to
. The vector f is set to 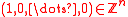 for
for  equal to a power of 2, so that the corresponding polynomial
equal to a power of 2, so that the corresponding polynomial  is irreducible
is irreducibleIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
.
Let
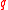 be a prime number
be a prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
such that
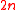 divides
divides 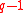 , and let
, and let  be an invertible matrix over
be an invertible matrix over 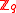 to be chosen later. The SWIFFT
to be chosen later. The SWIFFTSWIFFT
In cryptography, SWIFFT is a collection of provably secure hash functions. It is based on the concept of the Fast Fourier Transform . SWIFFT is not the first hash function based on FFT, but it sets itself apart by providing a mathematical proof of its security. It also uses the LLL basis reduction...
hash function
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
maps a key
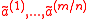 consisting of
consisting of 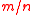 vectors chosen uniformly from
vectors chosen uniformly from 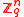 and an input
and an input  to
to 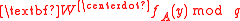 where
where 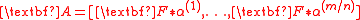 is as before and
is as before and  .
.Multiplication by the invertible matrix
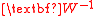 maps a uniformly chosen
maps a uniformly chosen 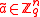 to a uniformly chosen
to a uniformly chosen 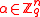 . Moreover,
. Moreover,  if and only if
if and only if 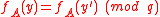 .
.Together, these two facts establish that finding collisions in SWIFFT
SWIFFT
In cryptography, SWIFFT is a collection of provably secure hash functions. It is based on the concept of the Fast Fourier Transform . SWIFFT is not the first hash function based on FFT, but it sets itself apart by providing a mathematical proof of its security. It also uses the LLL basis reduction...
is equivalent to finding collisions in the underlying ideal lattice function
 , and the claimed collision resistance
, and the claimed collision resistanceCollision resistance
Collision resistance is a property of cryptographic hash functions: a hash function is collision resistant if it is hard to find two inputs that hash to the same output; that is, two inputs a and b such that H = H, and a ≠ b.Every hash function with more inputs than outputs will necessarily have...
property of SWIFFT
SWIFFT
In cryptography, SWIFFT is a collection of provably secure hash functions. It is based on the concept of the Fast Fourier Transform . SWIFFT is not the first hash function based on FFT, but it sets itself apart by providing a mathematical proof of its security. It also uses the LLL basis reduction...
is supported by the connection to worst case lattice problems on ideal lattices.
The algorithm of the SWIFFT hash function is:
- Parameters: Integers
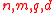 such that
such that  is a power of 2,
is a power of 2, 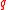 is prime,
is prime, 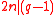 and
and  .
. - Key:
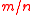 vectors
vectors 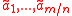 chosen independently and uniformly at random in
chosen independently and uniformly at random in 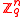 .
. - Input:
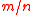 vectors
vectors 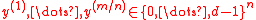 .
. - Output: the vector
 , where
, where  is the component-wise vector product.
is the component-wise vector product.
Ring-LWE
Learning with errors (LWE)Learning with errors
Learning with errors is a problem in machine learning. A generalization of the parity learning problem, it has recently been used to create public-key cryptosystems based on worst-case hardness of some lattice problems...
problem has been shown to be as hard as worst-case lattice problems and has served as the foundation for plenty of cryptographic applications. However, these applications are inefficient because of an inherent quadratic overhead in the use of LWE
Learning with errors
Learning with errors is a problem in machine learning. A generalization of the parity learning problem, it has recently been used to create public-key cryptosystems based on worst-case hardness of some lattice problems...
. To get truly efficient LWE
Learning with errors
Learning with errors is a problem in machine learning. A generalization of the parity learning problem, it has recently been used to create public-key cryptosystems based on worst-case hardness of some lattice problems...
applications, Lyubashevsky, Peikert and Regev defined an appropriate version of the LWE
Learning with errors
Learning with errors is a problem in machine learning. A generalization of the parity learning problem, it has recently been used to create public-key cryptosystems based on worst-case hardness of some lattice problems...
problem in a wide class of rings and proved its hardness under worst-case assumptions on ideal lattices in these rings. They called their LWE
Learning with errors
Learning with errors is a problem in machine learning. A generalization of the parity learning problem, it has recently been used to create public-key cryptosystems based on worst-case hardness of some lattice problems...
version ring-LWE.
Let
 , where the security parameter
, where the security parameter  is a power of 2, making
is a power of 2, making 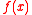 irreducible over the rationals. (This particular
irreducible over the rationals. (This particular 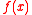 comes from the family of cyclotomic polynomial
comes from the family of cyclotomic polynomialCyclotomic polynomial
In algebra, the nth cyclotomic polynomial, for any positive integer n, is the monic polynomial:\Phi_n = \prod_\omega \,where the product is over all nth primitive roots of unity ω in a field, i.e...
s, which play a special role in this work).
Let
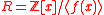 be the ring of integer polynomials modulo
be the ring of integer polynomials modulo  . Elements of
. Elements of  (i.e., residues modulo
(i.e., residues modulo 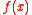 ) are typically represented by integer polynomials of degree less than
) are typically represented by integer polynomials of degree less than  . Let
. Let  be a sufficiently large public prime modulus (bounded by a polynomial in
be a sufficiently large public prime modulus (bounded by a polynomial in  ), and let
), and let 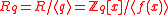 be the ring of integer polynomials modulo both
be the ring of integer polynomials modulo both 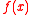 and
and 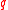 . Elements of
. Elements of 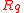 may be represented by polynomials of degree less than
may be represented by polynomials of degree less than  -whose coefficients are from
-whose coefficients are from 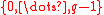 .
.In the above-described ring, the R-LWE problem may be described as follows.
Let
 be a uniformly random ring element, which is kept secret. Analogously to standard LWE, the goal of the attacker is to distinguish arbitrarily many (independent) ‘random noisy ring equations’ from truly uniform ones. More specifically, the noisy equations are of the form
be a uniformly random ring element, which is kept secret. Analogously to standard LWE, the goal of the attacker is to distinguish arbitrarily many (independent) ‘random noisy ring equations’ from truly uniform ones. More specifically, the noisy equations are of the form 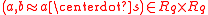 , where a is uniformly random and the product
, where a is uniformly random and the product  is perturbed by some ‘small’ random error term, chosen from a certain distribution over
is perturbed by some ‘small’ random error term, chosen from a certain distribution over  .
.They gave a quantum reduction from approximate SVP (in the worst case) on ideal lattices in
 to the search version of ring-LWE, where the goal is to recover the secret
to the search version of ring-LWE, where the goal is to recover the secret 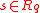 (with high probability, for any
(with high probability, for any  ) from arbitrarily many noisy products. This result follows the general outline of Regev’s iterative quantum reduction for general lattices, but ideal lattices introduce several new technical roadblocks in both the ‘algebraic’ and ‘geometric’ components of the reduction. They used algebraic number theory, in particular, the canonical embedding of a number field and the Chinese Remainder Theorem
) from arbitrarily many noisy products. This result follows the general outline of Regev’s iterative quantum reduction for general lattices, but ideal lattices introduce several new technical roadblocks in both the ‘algebraic’ and ‘geometric’ components of the reduction. They used algebraic number theory, in particular, the canonical embedding of a number field and the Chinese Remainder TheoremChinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
to overcome these obstacles. They got the following theorem:
Theorem Let
 be an arbitrary number field of degree
be an arbitrary number field of degree  . Let
. Let 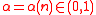 be arbitrary, and let the (rational) integer modulus
be arbitrary, and let the (rational) integer modulus 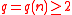 be such that
be such that 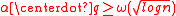 . There is a probabilistic polynomial-time quantum reduction from
. There is a probabilistic polynomial-time quantum reduction from  -
-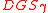 to
to 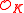 -
- 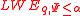 , where
, where  .
.Ideal-LWE
Stehle, Steinfeld, Tanaka and Xagawa defined a structured variant of LWE problem (Ideal-LWE) to describe an efficient public key encryption scheme based on the worst case hardness of the approximate SVP in ideal lattices. This is the first CPA-secure public key encryption scheme whose security relies on the hardness of the worst-case instances of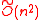 -Ideal-SVP against subexponential quantum attacks. It achieves asymptotically optimal efficiency: the public/private key length is
-Ideal-SVP against subexponential quantum attacks. It achieves asymptotically optimal efficiency: the public/private key length is 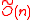 bits and the amortized encryption/decryption cost is
bits and the amortized encryption/decryption cost is  bit operations per message bit (encrypting
bit operations per message bit (encrypting 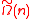 bits at once, at a
bits at once, at a 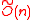 cost). The security assumption here is that
cost). The security assumption here is that 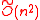 -Ideal-SVP cannot be solved by any subexponential time quantum algorithm. It is noteworthy that this is stronger than standard public key cryptography
-Ideal-SVP cannot be solved by any subexponential time quantum algorithm. It is noteworthy that this is stronger than standard public key cryptographyPublic-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
security assumptions. On the other hand, contrary to the most of public key cryptography
Public-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
, lattice-based cryptography allows security against subexponential quantum attacks.
Most of the cryptosystems based on general lattices rely on the average-case hardness of the Learning with errors (LWE)
Learning with errors
Learning with errors is a problem in machine learning. A generalization of the parity learning problem, it has recently been used to create public-key cryptosystems based on worst-case hardness of some lattice problems...
. Their scheme is based on a structured variant of LWE, that they call Ideal-LWE. They needed to introduce some techniques to circumvent two main difficulties that arise from the restriction to ideal lattices. Firstly, the previous cryptosystems based on unstructured lattices all make use of Regev’s worst-case to average-case classical reduction from Bounded Distance Deconding problem (BDD) to LWE
Learning with errors
Learning with errors is a problem in machine learning. A generalization of the parity learning problem, it has recently been used to create public-key cryptosystems based on worst-case hardness of some lattice problems...
(this is the classical step in the quantum reduction from SVP to LWE
Learning with errors
Learning with errors is a problem in machine learning. A generalization of the parity learning problem, it has recently been used to create public-key cryptosystems based on worst-case hardness of some lattice problems...
). This reduction exploits the unstructured-ness of the considered lattices, and does not seem to carry over to the structured lattices involved in Ideal-LWE. In particular, the probabilistic independence of the rows of the LWE matrices allows to consider a single row. Secondly, the other ingredient used in previous cryptosystems, namely Regev’s reduction from the computational variant of LWE
Learning with errors
Learning with errors is a problem in machine learning. A generalization of the parity learning problem, it has recently been used to create public-key cryptosystems based on worst-case hardness of some lattice problems...
to its decisional variant, also seems to fail for Ideal-LWE: it relies on the probabilistic independence of the columns of the LWE
Learning with errors
Learning with errors is a problem in machine learning. A generalization of the parity learning problem, it has recently been used to create public-key cryptosystems based on worst-case hardness of some lattice problems...
matrices.
To overcome these difficulties, they avoided the classical step of the reduction. Instead, they used the quantum step to construct a new quantum average-case reduction from SIS (average-case collision-finding problem) to LWE
Learning with errors
Learning with errors is a problem in machine learning. A generalization of the parity learning problem, it has recently been used to create public-key cryptosystems based on worst-case hardness of some lattice problems...
. It also works from Ideal-SIS to Ideal-LWE. Combined with the reduction from worst-case Ideal-SVP to average-case Ideal-SIS, they obtained the a quantum reduction from Ideal-SVP to Ideal-LWE. This shows the hardness of the computational variant of Ideal-LWE. Because they did not obtain the hardness of the decisional variant, they used a generic hardcore function to derive pseudorandom bits for encryption. This is why they needed to assume the exponential hardness of SVP.
Fully homomorphic encryption
An encryption is homomorphic for circuits in
is homomorphic for circuits in 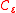 if
if  is correct for
is correct for  and
and  can be expressed as a circuit
can be expressed as a circuit 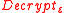 of size
of size 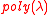 .
.  is fully homomorphic if it is homomorphic for all circuits. A fully homomorphic encryption
is fully homomorphic if it is homomorphic for all circuits. A fully homomorphic encryptionHomomorphic encryption
Homomorphic encryption is a form of encryption where a specific algebraic operation performed on the plaintext is equivalent to another algebraic operation performed on the ciphertext. Depending on one's viewpoint, this can be seen as either a positive or negative attribute of the cryptosystem....
scheme is the one which allows one to evaluate circuits over encrypted data without being able to decrypt. Gentry proposed a solution to the problem of constructing a fully homomorphic encryption
Homomorphic encryption
Homomorphic encryption is a form of encryption where a specific algebraic operation performed on the plaintext is equivalent to another algebraic operation performed on the ciphertext. Depending on one's viewpoint, this can be seen as either a positive or negative attribute of the cryptosystem....
scheme, which was introduced by Rivest, Adleman and Dertouzos shortly after the invention of RSA by Rivest, Adleman and Shamir in 1978. His scheme was based on ideal lattices.

