
Hermite normal form
Encyclopedia
In linear algebra
, the Hermite normal form is an analogue of reduced echelon form for matrices
over the integer
s Z.
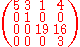
is in HNF.
such that the first r columns of M are zero, and for r + 1 ≤ j ≤ n
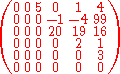
Here we have r=2; f(3)=1, f(4)=3, f(5)=4, f(6)=5.
(f(j) gives the row of the lowest nonzero entry in column j.)
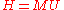 with U ∈ GLn(Z) (i.e. U is unimodular
with U ∈ GLn(Z) (i.e. U is unimodular
).
The matrix formed by the nonzero columns of H is called the Hermite normal form of M.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the Hermite normal form is an analogue of reduced echelon form for matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
over the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s Z.
Nonsingular square matrices
A nonsingular square matrix M = (mij) with integer entries is in Hermite normal form (HNF) if- M is upper triangular,
- its diagonal entries, mii, are positive,
- for j > i, mii > mij ≥ 0, i.e. in a given row, the entries to the right of the diagonal are less than the diagonal, and at least zero.
Example
The matrix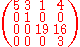
is in HNF.
General matrices
More generally, an m×n matrix with integer entries is in (HNF) if there exists- r with 0 ≤ r ≤ n,
- a strictly increasing function f: [r + 1, n] → [1, m],
such that the first r columns of M are zero, and for r + 1 ≤ j ≤ n
- mf(j)j > 0,
- mij = 0 when i > f(j),
- mf(j)j > mf(j)k ≥ 0 when k > j.
Example
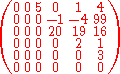
Here we have r=2; f(3)=1, f(4)=3, f(5)=4, f(6)=5.
(f(j) gives the row of the lowest nonzero entry in column j.)
Uniqueness of the Hermite normal form
Given any m×n matrix M with integer entries, there is a unique m×n matrix H, in HNF, with integer entries such that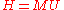 with U ∈ GLn(Z) (i.e. U is unimodular
with U ∈ GLn(Z) (i.e. U is unimodularUnimodular matrix
In mathematics, a unimodular matrix M is a square integer matrix with determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N which is its inverse...
).
The matrix formed by the nonzero columns of H is called the Hermite normal form of M.

