
Hurwitz's automorphisms theorem
Encyclopedia
In mathematics
, Hurwitz's automorphisms theorem bounds the order of the group of automorphism
s, via orientation-preserving conformal mappings, of a compact Riemann surface
of genus
g > 1, stating that the number of such automorphisms cannot exceed 84(g−1). A group for which the maximum is achieved is called a Hurwitz group, and the corresponding Riemann surface a Hurwitz surface
. Because compact Riemann surfaces are synonymous with non-singular complex projective algebraic curves
, a Hurwitz surface can also be called a Hurwitz curve. The theorem is named after Adolf Hurwitz
, who proved it in .
s of positive, zero, and negative curvature
K. It manifests itself in many diverse situations and on several levels. In the context of compact Riemann surfaces X, via the Riemann uniformization theorem
, this can be seen as a distinction between the surfaces of different topologies:
While in the first two cases the surface X admits infinitely many conformal automorphisms (in fact, the conformal automorphism group is a complex Lie group
of dimension three for a sphere and of dimension one for a torus), a hyperbolic Riemann surface only admits a discrete set of automorphisms. Hurwitz's theorem claims that in fact more is true: it provides a uniform bound on the order of the automorphism group as a function of the genus and characterizes those Riemann surfaces for which the bound is sharp.
. The conformal mappings of the surface correspond to orientation-preserving automorphisms of the hyperbolic plane. By the Gauss-Bonnet theorem, the area of the surface is
In order to make the automorphism group G of X as large as possible, we want the area of its fundamental domain
D for this action to be as small as possible. If the fundamental domain is a triangle with the vertex angles π/p, π/q and π/r, defining a tiling
of the hyperbolic plane, then p, q, and r are integers greater than one, and the area is
Thus we are asking for integers which make the expression
strictly positive and as small as possible. A remarkable fact is that this minimal value is 1/42, and
gives a unique (up to permutation) triple of such integers. This would indicate that the order |G| of the automorphism group is bounded by
However, a more delicate reasoning shows that this is an overestimate by the factor of two, because the group G can contain orientation-reversing transformations. For the orientation-preserving conformal automorphisms the bound is 84(g − 1).
 To obtain an example of a Hurwitz group, let us start with a (2,3,7)-tiling of the hyperbolic plane. Its full symmetry group is the full (2,3,7) triangle group
To obtain an example of a Hurwitz group, let us start with a (2,3,7)-tiling of the hyperbolic plane. Its full symmetry group is the full (2,3,7) triangle group
generated by the reflections across the sides of a single fundamental triangle with the angles π/2, π/3 and π/7. Since a reflection flips the triangle and changes the orientation, we can join the triangles in pairs and obtain an orientation-preserving tiling polygon.
A Hurwitz surface is obtained by 'closing up' a part of this infinite tiling of the hyperbolic plane to a compact Riemann surface of genus g. This will necessarily involve exactly 84(g − 1) double triangle tiles.
The following two regular tilings have the desired symmetry group; the rotational group corresponds to rotation about an edge, a vertex, and a face, while the full symmetry group would also include a reflection. Note that the polygons in the tiling are not fundamental domains – the tiling by (2,3,7) triangles refines both of these and is not regular.
Wythoff construction
s yields further uniform tiling
s, yielding eight uniform tilings, including the two regular ones given here. These all descend to Hurwitz surfaces, yielding tilings of the surfaces (triangulation, tiling by heptagons, etc.).
From the arguments above it can be inferred that a Hurwitz group G is characterized by the property that it is a finite quotient of the group with two generators a and b and three relations
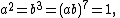
thus G is a finite group generated by two elements of orders two and three, whose product is of order seven. More precisely, any Hurwitz surface, that is, a hyperbolic surface that realizes the maximum order of the automorphism group for the surfaces of a given genus, can be obtained by the construction given.
This is the last part of the theorem of Hurwitz.
 The smallest Hurwitz group is the projective special linear group PSL(2,7)
The smallest Hurwitz group is the projective special linear group PSL(2,7)
, of order 168, and the corresponding curve is the Klein quartic curve
. This group is also isomorphic to PSL(3,2)
.
Next is the Macbeath curve
, with automorphism group PSL(2,8) of order 504. Many more finite simple groups are Hurwitz groups; for instance all but 64 of the alternating groups are Hurwitz groups, the largest non-Hurwitz example being of degree 167. The smallest alternating group that is a Hurwitz group is A15.
Most projective special linear groups of large rank are Hurwitz groups, . For lower ranks, fewer such groups are Hurwitz. For np the order of p modulo 7, one has that PSL(2,q) is Hurwitz if and only if either q=7 or q = pnp. Indeed, PSL(3,q) is Hurwitz if and only if q = 2, PSL(4,q) is never Hurwitz, and PSL(5,q) is Hurwitz if and only if q = 74 or q = pnp, .
Similarly, many groups of Lie type
are Hurwitz. The finite classical group
s of large rank are Hurwitz, . The exceptional Lie groups of type G2 and the Ree groups of type 2G2 are nearly always Hurwitz, . Other families of exceptional and twisted Lie groups of low rank are shown to be Hurwitz in .
There are 12 sporadic groups that can be generated as Hurwitz groups: the Janko group
s J1, J2 and J4, the Fischer group
s Fi22 and Fi'24, the Rudvalis group
, the Held group
, the Thompson group
, the Harada–Norton group,the third Conway group
Co3, the Lyons group
, and the Monster
, .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Hurwitz's automorphisms theorem bounds the order of the group of automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s, via orientation-preserving conformal mappings, of a compact Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
of genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
g > 1, stating that the number of such automorphisms cannot exceed 84(g−1). A group for which the maximum is achieved is called a Hurwitz group, and the corresponding Riemann surface a Hurwitz surface
Hurwitz surface
In Riemann surface theory and hyperbolic geometry, a Hurwitz surface, named after Adolf Hurwitz, is a compact Riemann surface with preciselyautomorphisms, where g is the genus of the surface. This number is maximal by virtue of Hurwitz's theorem on automorphisms...
. Because compact Riemann surfaces are synonymous with non-singular complex projective algebraic curves
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
, a Hurwitz surface can also be called a Hurwitz curve. The theorem is named after Adolf Hurwitz
Adolf Hurwitz
Adolf Hurwitz was a German mathematician.-Early life:He was born to a Jewish family in Hildesheim, former Kingdom of Hannover, now Lower Saxony, Germany, and died in Zürich, in Switzerland. Family records indicate that he had siblings and cousins, but their names have yet to be confirmed...
, who proved it in .
Interpretation in terms of hyperbolicity
One of the fundamental themes in differential geometry is a trichotomy between the Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s of positive, zero, and negative curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
K. It manifests itself in many diverse situations and on several levels. In the context of compact Riemann surfaces X, via the Riemann uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
, this can be seen as a distinction between the surfaces of different topologies:
- X a sphereRiemann sphereIn mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, a compact Riemann surface of genus zero with K > 0; - X a flat torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, or an elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
, a Riemann surface of genus one with K = 0; - and X a hyperbolic surface, which has genus greater than one and K < 0.
While in the first two cases the surface X admits infinitely many conformal automorphisms (in fact, the conformal automorphism group is a complex Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of dimension three for a sphere and of dimension one for a torus), a hyperbolic Riemann surface only admits a discrete set of automorphisms. Hurwitz's theorem claims that in fact more is true: it provides a uniform bound on the order of the automorphism group as a function of the genus and characterizes those Riemann surfaces for which the bound is sharp.
The idea of a proof and construction of the Hurwitz surfaces
By the uniformization theorem, any hyperbolic surface X – i.e., the Gaussian curvature of X is equal to negative one at every point – is covered by the hyperbolic planeHyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
. The conformal mappings of the surface correspond to orientation-preserving automorphisms of the hyperbolic plane. By the Gauss-Bonnet theorem, the area of the surface is
- A(X) = − 2π χ(X) = 4π(g − 1).
In order to make the automorphism group G of X as large as possible, we want the area of its fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
D for this action to be as small as possible. If the fundamental domain is a triangle with the vertex angles π/p, π/q and π/r, defining a tiling
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the hyperbolic plane, then p, q, and r are integers greater than one, and the area is
- A(D) = π(1 − 1/p − 1/q − 1/r).
Thus we are asking for integers which make the expression
- 1 − 1/p − 1/q − 1/r
strictly positive and as small as possible. A remarkable fact is that this minimal value is 1/42, and
- 1 − 1/2 − 1/3 − 1/7 = 1/42
gives a unique (up to permutation) triple of such integers. This would indicate that the order |G| of the automorphism group is bounded by
- A(X)/A(D) ≤ 168(g − 1).
However, a more delicate reasoning shows that this is an overestimate by the factor of two, because the group G can contain orientation-reversing transformations. For the orientation-preserving conformal automorphisms the bound is 84(g − 1).
Construction

(2,3,7) triangle group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
generated by the reflections across the sides of a single fundamental triangle with the angles π/2, π/3 and π/7. Since a reflection flips the triangle and changes the orientation, we can join the triangles in pairs and obtain an orientation-preserving tiling polygon.
A Hurwitz surface is obtained by 'closing up' a part of this infinite tiling of the hyperbolic plane to a compact Riemann surface of genus g. This will necessarily involve exactly 84(g − 1) double triangle tiles.
The following two regular tilings have the desired symmetry group; the rotational group corresponds to rotation about an edge, a vertex, and a face, while the full symmetry group would also include a reflection. Note that the polygons in the tiling are not fundamental domains – the tiling by (2,3,7) triangles refines both of these and is not regular.
 order-3 heptagonal tiling |
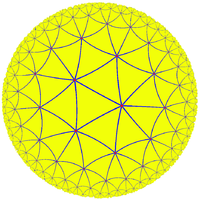 order-7 triangular tiling |
Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
s yields further uniform tiling
Uniform tiling
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-uniform.Uniform tilings can exist in both the Euclidean plane and hyperbolic plane...
s, yielding eight uniform tilings, including the two regular ones given here. These all descend to Hurwitz surfaces, yielding tilings of the surfaces (triangulation, tiling by heptagons, etc.).
From the arguments above it can be inferred that a Hurwitz group G is characterized by the property that it is a finite quotient of the group with two generators a and b and three relations
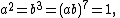
thus G is a finite group generated by two elements of orders two and three, whose product is of order seven. More precisely, any Hurwitz surface, that is, a hyperbolic surface that realizes the maximum order of the automorphism group for the surfaces of a given genus, can be obtained by the construction given.
This is the last part of the theorem of Hurwitz.
Examples of Hurwitz's groups and surfaces

PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
, of order 168, and the corresponding curve is the Klein quartic curve
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
. This group is also isomorphic to PSL(3,2)
PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
.
Next is the Macbeath curve
Macbeath surface
In Riemann surface theory and hyperbolic geometry, the Macbeath surface, also called Macbeath's curve or the Fricke–Macbeath curve, is the genus-7 Hurwitz surface....
, with automorphism group PSL(2,8) of order 504. Many more finite simple groups are Hurwitz groups; for instance all but 64 of the alternating groups are Hurwitz groups, the largest non-Hurwitz example being of degree 167. The smallest alternating group that is a Hurwitz group is A15.
Most projective special linear groups of large rank are Hurwitz groups, . For lower ranks, fewer such groups are Hurwitz. For np the order of p modulo 7, one has that PSL(2,q) is Hurwitz if and only if either q=7 or q = pnp. Indeed, PSL(3,q) is Hurwitz if and only if q = 2, PSL(4,q) is never Hurwitz, and PSL(5,q) is Hurwitz if and only if q = 74 or q = pnp, .
Similarly, many groups of Lie type
Group of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
are Hurwitz. The finite classical group
Classical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
s of large rank are Hurwitz, . The exceptional Lie groups of type G2 and the Ree groups of type 2G2 are nearly always Hurwitz, . Other families of exceptional and twisted Lie groups of low rank are shown to be Hurwitz in .
There are 12 sporadic groups that can be generated as Hurwitz groups: the Janko group
Janko group
In mathematics, a Janko group is one of the four sporadic simple groups named for Zvonimir Janko. Janko constructed the first Janko group J1 in 1965. At the same time, Janko also predicted the existence of J2 and J3. In 1976, he suggested the existence of J4...
s J1, J2 and J4, the Fischer group
Fischer group
In mathematics, the Fischer groups are the three sporadic simple groups Fi22, Fi23,Fi24' introduced by .- 3-transposition groups :...
s Fi22 and Fi'24, the Rudvalis group
Rudvalis group
In the mathematical field of group theory, the Rudvalis group Ru is a sporadic simple group of order-Properties:The Rudvalis group acts as a rank 3 permutation group on 4060 points, with one point stabilizer the Ree group...
, the Held group
Held group
In the mathematical field of group theory, the Held group He is one of the 26 sporadic simple groups, and has order...
, the Thompson group
Thompson group (finite)
In the mathematical field of group theory, the Thompson group Th, found by and constructed by , is a sporadic simple group of orderThe centralizer of an element of order 3 of type 3C in the Monster group is a product of the Thompson group and a group of order 3, as a result of which the Thompson...
, the Harada–Norton group,the third Conway group
Conway group
In mathematics, the Conway groups Co1, Co2, and Co3 are three sporadic groups discovered by John Horton Conway.The largest of the Conway groups, Co1, of order...
Co3, the Lyons group
Lyons group
In the mathematical field of group theory, the Lyons group Ly , is a sporadic simple group of order...
, and the Monster
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
, .

