
Held group
Encyclopedia
In the mathematical field of group theory
, the Held group He (found by Dieter Held (1969)) is one of the 26 sporadic
simple group
s, and has order
It can be defined in terms of the generators a and b and relations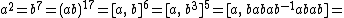
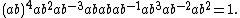
It was found by Held during an investigation of simple groups containing an involution whose centralizer is isomorphic to that of an involution in the Mathieu group M24. A second such group is the linear group
L5(2). The Held group is the third possibility, and its construction was completed by John McKay
and Graham Higman
.
The Held group has Schur multiplier
of order 1 and outer automorphism group of order 2.
It centralizes an element of order 7 in the Monster group
(but is not a subgroup
of any of the Conway groups). As a result the prime 7 plays a special role in the theory of the group; for example, the smallest representation of the Held group over any field is the 50 dimensional representation over the field with 7 elements, and it acts naturally on a vertex operator algebra
over the field with 7 elements.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Held group He (found by Dieter Held (1969)) is one of the 26 sporadic
Sporadic group
In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s, and has order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
- 210 · 33 · 52 · 73 · 17
- = 4030387200
- ≈ 4 · 109.
It can be defined in terms of the generators a and b and relations
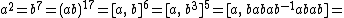
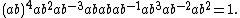
It was found by Held during an investigation of simple groups containing an involution whose centralizer is isomorphic to that of an involution in the Mathieu group M24. A second such group is the linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
L5(2). The Held group is the third possibility, and its construction was completed by John McKay
John McKay (mathematician)
John McKay is a dual British/Canadian citizen, a mathematician at Concordia University, known for his discovery of monstrous moonshine, his joint construction of some sporadic simple groups, for the McKay conjecture in representation theory, and for the McKay correspondence relating certain...
and Graham Higman
Graham Higman
Graham Higman FRS was a leading British mathematician. He is known for his contributions to group theory....
.
The Held group has Schur multiplier
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
of order 1 and outer automorphism group of order 2.
It centralizes an element of order 7 in the Monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
(but is not a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of any of the Conway groups). As a result the prime 7 plays a special role in the theory of the group; for example, the smallest representation of the Held group over any field is the 50 dimensional representation over the field with 7 elements, and it acts naturally on a vertex operator algebra
Vertex operator algebra
In mathematics, a vertex operator algebra is an algebraic structure that plays an important role in conformal field theory and related areas of physics...
over the field with 7 elements.

