Homography
Encyclopedia
Homography is a concept in the mathematical
science of geometry
.
A homography is an invertible transformation from a projective space (for example, the real projective plane
) to itself that maps straight lines to straight lines. Synonyms are collineation, projective transformation, and projectivity, though "collineation" is also used more generally.
Formally, a projective transformation in a plane is a transformation
used in projective geometry
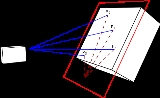
: it is the composition of a pair of perspective projections. It describes what happens to the perceived positions of observed objects when the point of view of the observer changes. Projective transformations do not preserve sizes or angles but do preserve incidence
and cross-ratio
: two properties which are important in projective geometry. Projectivities form a group
.
For more general projective space
s – of different dimensions or over different fields
– "homography" means a projective linear transformation (an invertible transformation induced by a linear transformation of the associated vector space), while "collineation
" (meaning "maps lines to lines") is more general, and includes both homographies and automorphic collineations (collineations induced by a field automorphism), as well as combinations of these.
, any two images of the same planar surface in space are related by a homography (assuming a pinhole camera model
). This has many practical applications, such as image rectification
, image registration
, or computation of camera motion—rotation and translation—between two images. Once camera rotation and translation have been extracted from an estimated homography matrix, this information may be used for navigation, or to insert models of 3D objects into an image or video, so that they are rendered with the correct perspective and appear to have been part of the original scene (see Augmented Reality
).
in a plane.
Passing the projections of
from 
in b to a point 
in a:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
science of geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
.
A homography is an invertible transformation from a projective space (for example, the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
) to itself that maps straight lines to straight lines. Synonyms are collineation, projective transformation, and projectivity, though "collineation" is also used more generally.
Formally, a projective transformation in a plane is a transformation
Transformation (mathematics)
In mathematics, a transformation could be any function mapping a set X on to another set or on to itself. However, often the set X has some additional algebraic or geometric structure and the term "transformation" refers to a function from X to itself that preserves this structure.Examples include...
used in projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
: it is the composition of a pair of perspective projections. It describes what happens to the perceived positions of observed objects when the point of view of the observer changes. Projective transformations do not preserve sizes or angles but do preserve incidence
Incidence (geometry)
In geometry, the relations of incidence are those such as 'lies on' between points and lines , and 'intersects' . That is, they are the binary relations describing how subsets meet...
and cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
: two properties which are important in projective geometry. Projectivities form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
For more general projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
s – of different dimensions or over different fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
– "homography" means a projective linear transformation (an invertible transformation induced by a linear transformation of the associated vector space), while "collineation
Collineation
In projective geometry, a collineation is a one-to-one and onto map from one projective space to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. All projective linear transformations induce a collineation...
" (meaning "maps lines to lines") is more general, and includes both homographies and automorphic collineations (collineations induced by a field automorphism), as well as combinations of these.
Computer vision applications
In the field of computer visionComputer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, any two images of the same planar surface in space are related by a homography (assuming a pinhole camera model
Pinhole camera model
The pinhole camera model describes the mathematical relationship between the coordinates of a 3D point and its projection onto the image plane of an ideal pinhole camera, where the camera aperture is described as a point and no lenses are used to focus light...
). This has many practical applications, such as image rectification
Image rectification
Image rectification is a transformation process used to project two-or-more images onto a common image plane. It corrects image distortion by transforming the image into a standard coordinate system....
, image registration
Image registration
Image registration is the process of transforming different sets of data into one coordinate system. Data may be multiple photographs, data from different sensors, from different times, or from different viewpoints. It is used in computer vision, medical imaging, military automatic target...
, or computation of camera motion—rotation and translation—between two images. Once camera rotation and translation have been extracted from an estimated homography matrix, this information may be used for navigation, or to insert models of 3D objects into an image or video, so that they are rendered with the correct perspective and appear to have been part of the original scene (see Augmented Reality
Augmented reality
Augmented reality is a live, direct or indirect, view of a physical, real-world environment whose elements are augmented by computer-generated sensory input such as sound, video, graphics or GPS data. It is related to a more general concept called mediated reality, in which a view of reality is...
).
3D plane to plane equation
We have two cameras a and b, looking at points in a plane.Passing the projections of
from in b to a point in a:-
where
is
is the rotation matrix by which b is rotated in relation to a; t is the translation vector from a to b; n and d are the normal vector of the plane and the distance to the plane respectively.
Ka and Kb are the cameras' intrinsic parameter matrices.
The figure shows camera b looking at the plane at distance d.
Note: From above figure,
is the projection of vector 
into 
, and equal to d. So 
. And we have 
.
Mathematical definition
In the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, a Mobius transformation is frequently called a homography. These linear-fractional transformations are expressions of projective transformations on the complex projective line, an extension of the complex plane.
In higher dimensions
Homogeneous coordinatesHomogeneous coordinatesIn mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
are used to represent projective transformations by means of matrix multiplications. With Cartesian coordinates matrix multiplication cannot perform the division required for perspective projection. In other words, with Cartesian coordinates a perspective projection is a non-linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
.
Given:
Then:
where:
Also:
Affine homography
When the image region in which the homography is computed is small or the image has been acquired with a large focal length, an affine homography is a more appropriate model of image displacements. An affine homography is a special type of a general homography whose last row is fixed to
External links
- M. Lourakis' homest is a GPL CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
/C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
library for robustRobust statisticsRobust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
, non-linear (based on the Levenberg-Marquardt algorithmLevenberg-Marquardt algorithmIn mathematics and computing, the Levenberg–Marquardt algorithm provides a numerical solution to the problem of minimizing a function, generally nonlinear, over a space of parameters of the function...
) homography estimation from matched point pairs. homest can estimate fully projective and affine homographies with a variety of objective functions. - OpenCVOpenCVOpenCV is a library of programming functions mainly aimed at real time computer vision, developed by Intel and now supported by Willow Garage. It is free for use under the open source BSD license. The library is cross-platform. It focuses mainly on real-time image processing...
is a complete (open and free) computer vision software library that has many routines related to homography estimation (cvFindHomography) and re-projection (cvPerspectiveTransform). Download and documentation information is on the OpenCV Wiki. - Computing the plane to plane homography
- How to compute a homography
- MATLAB Functions for Multiple View Geometry MatlabMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
functions for calculating a homography and the fundamental matrix
-
