In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a homoclinic orbit is a trajectory of a flow

Flow (mathematics)

In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...

 of a dynamical system

Dynamical system

A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...

 which joins a saddle equilibrium point to itself. More precisely, a homoclinic orbit lies in the intersection of the stable manifold

Stable manifold

In mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...

 and the unstable manifold of an equilibrium.

Homoclinic orbits and homoclinic points are defined in the same way for iterated function

Iterated function

In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...

s, as the intersection of the stable set

Stable set

The term stable set may refer to:* The independent set in graph theory, the set of vertices of a graph not directly connected by edges.* The stable set in dynamical systems, the set of points leading up to an attractor....

 and unstable set of some fixed point

Fixed point (mathematics)

In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...

 or periodic point

Periodic point

In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...

 of the system.

Consider the continuous dynamical system described by the ODE


Suppose there is an equilibrium at 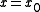, then a solution 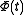is a homoclinic orbit if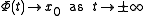


If the phase space

Phase space

In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...

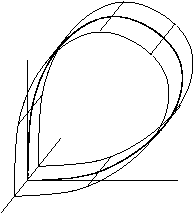
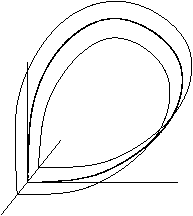
 has three or more dimensions, then it is important to consider the topology of the unstable manifold of the saddle point. The figures show two cases. First, when the unstable manifold is topologically a cylinder, and secondly, when the unstable manifold is topologically a Möbius strip

Möbius strip

The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...

; in this case the homoclinic orbit is called twisted.

We also have the notion of homoclinic orbit when considering discrete dynamical systems. In such a case, if 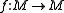is a diffeomorphism of a manifold 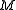, we say that is a homoclinic point if it has the same past and future - more specifically, if it exists a fixed (or periodic) point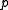
such that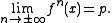

Properties

The existence of one homoclinic point implies the existence of infinite number of them.
This comes from its definition: the interception of a stable and unstable set. Both sets are invariant by definition, which means that the forward iteration of the homoclinic point is both on the stable and unstable set. By iterating N times, the map approaches the equilibrium point by the stable set, but in every iteration it is on the unstable manifold too, which shows this property.

This property suggests that complicated dynamics arise by the existence of a homoclinic point. Indeed, Smale (1967) showed that these points leads to horseshoe map

Horseshoe map

In the mathematics of chaos theory, a horseshoe map is any member of a class of chaotic maps of the square into itself. It is a core example in the study of dynamical systems. The map was introduced by Stephen Smale while studying the behavior of the orbits of the van der Pol oscillator...

 like dynamics, which is associated with chaos.

Symbolic dynamics

By using the Markov partition

Markov partition

A Markov partition is a tool used in dynamical systems theory, allowing the methods of symbolic dynamics to be applied to the study of hyperbolic systems. By using a Markov partition, the system can be made to resemble a discrete-time Markov process, with the long-term dynamical characteristics...

, the long-time behaviour of hyperbolic system can be studied using the techniques of symbolic dynamics

Symbolic dynamics

In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...

. In this case, a homoclinic orbit has a particularly simple and clear representation. Suppose that 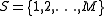is a finite set of M symbols. The dynamics of a point x is then represented by a bi-infinite string of symbols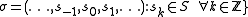


A periodic point

Periodic point

In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...

 of the system is simply a recurring sequence of letters. A heteroclinic orbit

Heteroclinic orbit

In mathematics, in the phase portrait of a dynamical system, a heteroclinic orbit is a path in phase space which joins two different equilibrium points...

is then the joining of two distinct periodic orbits. It may be written as


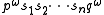
where 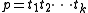is a sequence of symbols of length k, (of course, 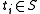), and 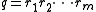is another sequence of symbols, of length m (likewise, 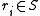). The notation 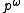simply denotes the repetition of p an infinite number of times. Thus, a heteroclinic orbit can be understood as the transition from one periodic orbit to another. By contrast, a homoclinic orbit can be written as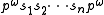


with the intermediate sequence 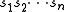being non-empty, and, of course, not being p, as otherwise, the orbit would simply be .

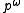External links

• Homoclinic orbits in Henon map with Java applets and comments