Positive invariant set
Encyclopedia
In mathematical analysis
, a positively invariant set is a set with the following properties:
Given a dynamical system
and trajectory
where 
is the initial point. Let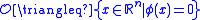 
where 
is a real valued function
. The set
is said to be positively invariant if 
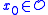implies that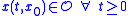 
Intuitively, this means that once a trajectory of the system enters
, it will never leave it again.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a positively invariant set is a set with the following properties:
Given a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
and trajectoryTrajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
where is the initial point. Let 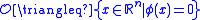where is a real valued functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. The set
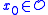is said to be positively invariant if implies that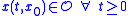 Intuitively, this means that once a trajectory of the system enters
, it will never leave it again.