
Rule of inference
Encyclopedia
In logic
, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form
of premise
s interpreted as a function which takes premises, analyses their syntax
, and returns a conclusion (or conclusions
). For example, the rule of inference modus ponens
takes two premises, one in the form of "If p then q" and another in the form of "p" and returns the conclusion "q". The rule is valid with respect to the semantics of classical logic
(as well as the semantics of many other non-classical logic
s), in the sense that if the premises are true (under an interpretation) then so is the conclusion.
Typically, a rule of inference preserves truth, a semantic property. In many-valued logic, it preserves a general designation. But a rule of inference's action is purely syntactic, and does not need to preserve any semantic property: any function from sets of formulae to formulae counts as a rule of inference. Usually only rules that are recursive
are important; i.e. rules such that there is an effective procedure for determining whether any given formula is the conclusion of a given set of formulae according to the rule. An example of a rule that is not effective in this sense is the infinitary ω-rule.
Popular rules of inference include modus ponens, modus tollens
from propositional logic and contraposition
. First-order predicate logic
uses rules of inference to deal with logical quantifiers. See List of rules of inference for examples.
(and many related areas), rules of inference are usually given in the following standard form:
Premise#1
Premise#2
...
Premise#n
Conclusion
This expression states, that whenever in the course of some logical derivation the given premises have been obtained, the specified conclusion can be taken for granted as well. The exact formal language that is used to describe both premises and conclusions depends on the actual context of the derivations. In a simple case, one may use logical formulae, such as in:
A→B
A
∴B
This is just the modus ponens rule of propositional logic. Rules of inference are usually formulated as rule schemata by the use of universal variables. In the rule (schema) above, A and B can be instantiated to any element of the universe (or sometimes, by convention, some restricted subset such as propositions) to form an infinite set of inference rules.
A proof system is formed from a set of rules chained together to form proofs, or derivations. Any derivation has only one final conclusion, which is the statement proved or derived. If premises are left unsatisfied in the derivation, then the derivation is a proof of a hypothetical statement: "if the premises hold, then the conclusion holds."
s (the judgment
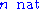 asserts the fact that
asserts the fact that  is a natural number):
is a natural number):
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form
Logical form
In logic, the logical form of a sentence or set of sentences is the form obtained by abstracting from the subject matter of its content terms or by regarding the content terms as mere placeholders or blanks on a form...
of premise
Premise
Premise can refer to:* Premise, a claim that is a reason for, or an objection against, some other claim as part of an argument...
s interpreted as a function which takes premises, analyses their syntax
Syntax (logic)
In logic, syntax is anything having to do with formal languages or formal systems without regard to any interpretation or meaning given to them...
, and returns a conclusion (or conclusions
Multiple-conclusion logic
A multiple-conclusion logic is one in which logical consequence is a relation, \vdash, between two sets of sentences . \Gamma \vdash \Delta is typically interpreted as meaning that whenever each element of \Gamma is true, some element of \Delta is true; and whenever each element of \Delta is...
). For example, the rule of inference modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
takes two premises, one in the form of "If p then q" and another in the form of "p" and returns the conclusion "q". The rule is valid with respect to the semantics of classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
(as well as the semantics of many other non-classical logic
Non-classical logic
Non-classical logics is the name given to formal systems which differ in a significant way from standard logical systems such as propositional and predicate logic. There are several ways in which this is done, including by way of extensions, deviations, and variations...
s), in the sense that if the premises are true (under an interpretation) then so is the conclusion.
Typically, a rule of inference preserves truth, a semantic property. In many-valued logic, it preserves a general designation. But a rule of inference's action is purely syntactic, and does not need to preserve any semantic property: any function from sets of formulae to formulae counts as a rule of inference. Usually only rules that are recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
are important; i.e. rules such that there is an effective procedure for determining whether any given formula is the conclusion of a given set of formulae according to the rule. An example of a rule that is not effective in this sense is the infinitary ω-rule.
Popular rules of inference include modus ponens, modus tollens
Modus tollens
In classical logic, modus tollens has the following argument form:- Formal notation :...
from propositional logic and contraposition
Contraposition
In traditional logic, contraposition is a form of immediate inference in which from a given proposition another is inferred having for its subject the contradictory of the original predicate, and in some cases involving a change of quality . For its symbolic expression in modern logic see the rule...
. First-order predicate logic
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
uses rules of inference to deal with logical quantifiers. See List of rules of inference for examples.
Overview
In formal logicFormal logic
Classical or traditional system of determining the validity or invalidity of a conclusion deduced from two or more statements...
(and many related areas), rules of inference are usually given in the following standard form:
Premise#1
Premise#2
...
Premise#n
Conclusion
This expression states, that whenever in the course of some logical derivation the given premises have been obtained, the specified conclusion can be taken for granted as well. The exact formal language that is used to describe both premises and conclusions depends on the actual context of the derivations. In a simple case, one may use logical formulae, such as in:
A→B
A
∴B
This is just the modus ponens rule of propositional logic. Rules of inference are usually formulated as rule schemata by the use of universal variables. In the rule (schema) above, A and B can be instantiated to any element of the universe (or sometimes, by convention, some restricted subset such as propositions) to form an infinite set of inference rules.
A proof system is formed from a set of rules chained together to form proofs, or derivations. Any derivation has only one final conclusion, which is the statement proved or derived. If premises are left unsatisfied in the derivation, then the derivation is a proof of a hypothetical statement: "if the premises hold, then the conclusion holds."
Admissibility and derivability
In a set of rules, an inference rule could be redundant in the sense that it is admissible or derivable. A derivable rule is one whose conclusion can be derived from its premises using the other rules. An admissible rule is one whose conclusion holds whenever the premises hold. All derivable rules are admissible. To appreciate the difference, consider the following set of rules for defining the natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s (the judgment
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
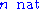 asserts the fact that
asserts the fact that  is a natural number):
is a natural number):-
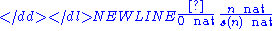
The first rule states that 0 is a natural number, and the second states that s(n) is a natural number if n is. In this proof system, the following rule demonstrating that the second successor of a natural number is also a natural number, is derivable:
-

Its derivation is just the composition of two uses of the successor rule above. The following rule for asserting the existence of a predecessor for any nonzero number is merely admissible:
-

This is a true fact of natural numbers, as can be proven by inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. (To prove that this rule is admissible, assume a derivation of the premise and induct on it to produce a derivation of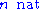 .) However, it is not derivable, because it depends on the structure of the derivation of the premise. Because of this, derivability is stable under additions to the proof system, whereas admissibility is not. To see the difference, suppose the following nonsense rule were added to the proof system:
.) However, it is not derivable, because it depends on the structure of the derivation of the premise. Because of this, derivability is stable under additions to the proof system, whereas admissibility is not. To see the difference, suppose the following nonsense rule were added to the proof system:
-

In this new system, the double-successor rule is still derivable. However, the rule for finding the predecessor is no longer admissible, because there is no way to derive . The brittleness of admissibility comes from the way it is proved: since the proof can induct on the structure of the derivations of the premises, extensions to the system add new cases to this proof, which may no longer hold.
. The brittleness of admissibility comes from the way it is proved: since the proof can induct on the structure of the derivations of the premises, extensions to the system add new cases to this proof, which may no longer hold.
Admissible rules can be thought of as theoremTheoremIn mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s of a proof system. For instance, in a sequent calculusSequent calculusIn proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
where cut elimination holds, the cut rule is admissible.
Other considerations
Inference rules may also be stated in this form: (1) some (perhaps zero) premises, (2) a turnstileTurnstile (symbol)In mathematical logic and computer science the symbol \vdash has taken the name turnstile because of its resemblance to a typical turnstile if viewed from above. It is also referred to as tee and is often read as "yields", "proves", "satisfies" or "entails"...
symbol , which means "infers", "proves" or "concludes", (3) a conclusion. This usually embodies the relational (as opposed to functional) view of a rule of inference, where the turnstile stands for a deducibility relation holding between premises and conclusion.
, which means "infers", "proves" or "concludes", (3) a conclusion. This usually embodies the relational (as opposed to functional) view of a rule of inference, where the turnstile stands for a deducibility relation holding between premises and conclusion.
Rules of inference must be distinguished from axiomAxiomIn traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s of a theory. In terms of semantics, axioms are valid assertions. Axioms are usually regarded as starting points for applying rules of inference and generating a set of conclusions. Or, in less technical terms:
Rules are statements ABOUT the system, axioms are statements IN the system. For example:- The RULE that from
 you can infer
you can infer 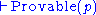 is a statement that says if you've proven p, then it is provable that p is provable. This holds in Peano arithmetic, for example.
is a statement that says if you've proven p, then it is provable that p is provable. This holds in Peano arithmetic, for example. - The Axiom
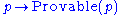 would mean that every true statement is provable. This does not hold in Peano arithmetic.
would mean that every true statement is provable. This does not hold in Peano arithmetic.
Rules of inference play a vital role in the specification of logical calculiFormal systemIn formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
as they are considered in proof theoryProof theoryProof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
, such as the sequent calculusSequent calculusIn proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
and natural deductionNatural deductionIn logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
.
See also
- Inference objectionInference objectionIn informal logic, an inference objection is an objection to an argument based not on any of its stated premises, but rather on the relationship between premise and contention. For a given simple argument, if the assumption is made that its premises are correct, fault may be found in the...
- Immediate inferenceImmediate inferenceAn immediate inference is an inference which can be made from only one statement or proposition. For instance, from the statement "All toads are green." we can make the immediate inference that "No toads are not green." This new statement is known as the contrapositive of the original statement...
- Law of thoughtLaw of thoughtThe laws of thought are fundamental axiomatic rules upon which rational discourse itself is based. The rules have a long tradition in the history of philosophy. They are laws that guide and underlie everyone's thinking, thoughts, expressions, discussions, etc.The three classic laws of thought are...
- Logical truthLogical truthLogical truth is one of the most fundamental concepts in logic, and there are different theories on its nature. A logical truth is a statement which is true and remains true under all reinterpretations of its components other than its logical constants. It is a type of analytic statement.Logical...
- The RULE that from
-
-
-

