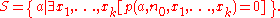Hilbert's tenth problem
Encyclopedia
Hilbert's tenth problem is the tenth on the list of Hilbert's problems
of 1900. Its statement is as follows:
A Diophantine equation
is an equation of the form

where p is a polynomial
with integer coefficients. It took many years for the problem to be solved with a negative answer. Today, it is known that no such algorithm exists in the general case. This result is the combined work of Martin Davis
, Yuri Matiyasevich
, Hilary Putnam
and Julia Robinson
.
. The term "rational integer" simply refers to the integers, positive, negative or zero: 0, ±1, ±2, ... . So Hilbert was asking for a general algorithm to decide whether a given polynomial Diophantine equation
with integer coefficients has a solution in integers. The answer to the problem is now known to be in the negative: no such general algorithm can exist. Although it is unlikely that Hilbert had conceived of such a possibility, before going on to list the problems, he did presciently remark:
The work on the problem has been in terms of solutions in natural numbers rather than arbitrary integers. But it is easy to see that an algorithm in either case could be used to obtain one for the other. If one possessed an algorithm to determine solvability in natural numbers, it could be used to determine whether an equation in unknowns,
unknowns,

has an integer solution by applying the supposed algorithm to the 2n equations

Conversely, an algorithm to test for solvability in arbitrary integers could be used to test a given equation for solvability in natural numbers by applying that supposed algorithm to the equation obtained from the given equation by replacing each unknown by the sum of the squares of four new unknowns. This works because of Lagrange's four-square theorem
, to the effect that every natural number can be written as the sum of four squares.
s.
Diophantine definitions can be provided by simultaneous systems of equations as well as by individual equations because the system

is equivalent to the single equation

A recursively enumerable set
can be characterized as one for which there exists an algorithm
that will ultimately halt when a member of the set is provided as input, but may continue indefinitely when the input is a non member. It was the development of computability theory
(also known as recursion theory
) that provided a precise explication of the intutitive notion of algorithmic computability, thus making the notion of recursive enumerability perfectly rigorous. It is evident that Diophantine sets are recursively enumerable. This is because one can arrange all possible tuples of values of the unknowns in a sequence and then, for a given value of the parameter(s), test these tuples, one after another, to see whether they are solutions of the corresponding equation. The unsolvability of Hilbert's tenth problem is a consequence of the surprising fact that the
converse is true:
This result is variously known as Matiyasevich's theorem (because he provided the crucial step that completed the proof) and the MRDP theorem (for Yuri Matiyasevich
, Julia Robinson
, Martin Davis
, and Hilary Putnam
). Because there exists a recursively enumerable set that is not computable, the unsolvability of Hilbert's tenth problem is an immediate consequence. In fact, more can be said: there is a polynomial
with integer coefficients such that the set of values of for which the equation
for which the equation
has solutions in natural numbers is not computable. So, not only is there no general algorithm for testing Diophantine equations for solvability, even for this one parameter family of equations, there is no algorithm.
This can be seen to be true simply because there are universal Turing machine
s, capable of executing any algorithm. This implication of J.R. had made it seem implausible.
Hilary Putnam has pointed out that for any Diophantine set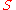 of positive integers, there is a polynomial
of positive integers, there is a polynomial

such that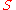 consists of exactly the positive numbers among the values assumed by
consists of exactly the positive numbers among the values assumed by 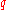 as
as
the variables

range over all natural numbers. This can be seen as follows: If

provides a Diophantine definition of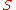 , then it suffices to set
, then it suffices to set
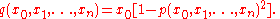
So, for example, there is a polynomial for which the positive part of its range is exactly the prime numbers. (On the other hand no polynomial can only take on prime values.)
Other applications concern what logicians refer to as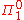 propositions, sometimes also called propositions of Goldbach type. These are like the Goldbach Conjecture, in stating that all natural numbers possess a certain property that is algorithmically checkable for each particular number. The Matiyasevich/MRDP Theorem implies that each such proposition is equivalent to a statement that asserts that some particular Diophantine equation has no solutions in natural numbers. A number of important and celebrated problems are of this form: in particular, Fermat's Last Theorem
propositions, sometimes also called propositions of Goldbach type. These are like the Goldbach Conjecture, in stating that all natural numbers possess a certain property that is algorithmically checkable for each particular number. The Matiyasevich/MRDP Theorem implies that each such proposition is equivalent to a statement that asserts that some particular Diophantine equation has no solutions in natural numbers. A number of important and celebrated problems are of this form: in particular, Fermat's Last Theorem
, the Riemann Hypothesis
, and the Four Color Theorem
. In addition the assertion that particular formal system
s such as Peano Arithmetic or ZFC are consistent can be expressed as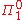 sentences. The idea is to follow Kurt Gödel
sentences. The idea is to follow Kurt Gödel
in coding proofs by natural numbers in such a way that the property of being the number representing a proof is algorithmically checkable.
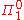 sentences have the special property that if they are false, that fact will be provable in any of the usual formal systems. This is because the falsity amounts to the existence of a counter-example which can be verified by simple arithmetic. So if a
sentences have the special property that if they are false, that fact will be provable in any of the usual formal systems. This is because the falsity amounts to the existence of a counter-example which can be verified by simple arithmetic. So if a 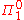 sentence is such that neither it nor its negation is provable in one of these systems, that sentence must be true.
sentence is such that neither it nor its negation is provable in one of these systems, that sentence must be true.
A particularly striking form of Gödel's incompleteness theorem is also a consequence of the Matiyasevich/MRDP Theorem:
Let

provide a Diophantine definition of a non-computable set. Let be an algorithm that outputs a sequence of natural numbers
be an algorithm that outputs a sequence of natural numbers  such that the corresponding equation
such that the corresponding equation

has no solutions in natural numbers. Then there is a number which is not output by
which is not output by  while in fact the equation
while in fact the equation

has no solutions in natural numbers.
To see that the theorem is true, it suffices to notice that if there were no such number , one could algorithmically test membership of a number
, one could algorithmically test membership of a number  in this non-computable set by simultaneously running the algorithm
in this non-computable set by simultaneously running the algorithm  to see whether
to see whether  is output while also checking all possible
is output while also checking all possible 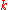 -tuples of natural numbers seeking a solution of the equation
-tuples of natural numbers seeking a solution of the equation
We may associate an algorithm with any of the usual formal systems such as Peano Arithmetic or ZFC by letting it systematically generate consequences of the axioms and then output a number
with any of the usual formal systems such as Peano Arithmetic or ZFC by letting it systematically generate consequences of the axioms and then output a number  whenever a sentence of the form
whenever a sentence of the form
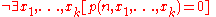
is generated. Then the theorem tells us that either a false statement of this form is proved or a true one remains unproved in the system in question.
Already in the 1920s Thoralf Skolem
showed that any Diophantine equation is equivalent to one of degree 4 or less. His trick was to introduce new unknowns by equations setting them equal to the square of an unknown or the product of two unknowns. Repetition of this process results in a system of second degree equations; then an equation of degree 4 is obtained by summing the squares. So every Diophantine set is trivially of degree 4 or less. It is not known whether this result is best possible.
Julia Robinson and Yuri Matiyasevich showed that every Diophantine set has dimension no greater than 13. Later, Matiyasevich sharpened their methods to show that 9 unknowns suffice. Although no one imagines that this striking result is the best possible, there has been no further progress. So, in particular, there is no algorithm for testing Diophantine equations with 9 or fewer unknowns for solvability in natural numbers. For the case of rational integer solutions (as Hilbert had originally posed it), the 4 squares trick shows that there is no algorithm for equations with no more than 36 unknowns. But Zhi Wei Sun showed that the problem for integers is unsolvable even for equations with no more than 11 unknowns.
Martin Davis studied algorithmic questions involving the number of solutions of a Diophantine equation. Hilbert's tenth problem asks whether or not that number is 0. Let
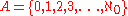 and let
and let  be a proper non-empty subset of
be a proper non-empty subset of  . Davis proved that there is no algorithm to test a given Diophantine equation to determine whether the number of its solutions is a member of the set
. Davis proved that there is no algorithm to test a given Diophantine equation to determine whether the number of its solutions is a member of the set  . Thus there is no algorithm to determine whether the number of solutions of a Diophantine equation
. Thus there is no algorithm to determine whether the number of solutions of a Diophantine equation
is finite, odd, a perfect square, a prime, etc.
s (in particular, for any ring whose elements are listable). Obvious examples are the rings of integers of algebraic number field
s as well as the rational numbers. An algorithm such as he was requesting could have been extended to cover these other domains. For example, the equation
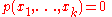
where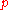 is a polynomial of degree
is a polynomial of degree 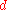 is solvable in non-negative rational numbers if and only if
is solvable in non-negative rational numbers if and only if
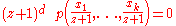
is solvable in natural numbers. (If one possessed an algorithm to determine solvability in non-negative rational numbers, it could easily be used to determine solvability in the rationals.) However, knowing that there is no such algorithm as Hilbert had desired says nothing about these other domains.
There has been much work on Hilbert's tenth problem for the rings of integers of algebraic number fields. Basing themselves on earlier work by Jan Denef
and Leonard Lipschitz and using class field theory, Harold N. Shapiro and Alexandra Shlapentokh were able to prove:
Shlapentokh and Thanases Pheidas (independently of one another) obtained the same result for algebraic number fields admitting exactly one pair of complex conjugate embeddings.
The problem for the ring of integers of algebraic number fields other than those covered by the results above remains open. Likewise, despite much interest, the problem for equations over the rationals remains open. Barry Mazur
has conjectured that for any variety
over the rationals, the topological closure over the reals of the set of solutions has only finitely many components. This conjecture implies that the integers are not Diophantine over the rationals and so if this conjecture is true a negative answer to Hilbert's Tenth Problem would require a different approach than that used for other rings.
Hilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
of 1900. Its statement is as follows:
Given a Diophantine equation with any number of unknown quantities and with rational integral numerical coefficients: To devise a process according to which it can be determined in a finite number of operations whether the equation is solvable in rational integers.
A Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
is an equation of the form

where p is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with integer coefficients. It took many years for the problem to be solved with a negative answer. Today, it is known that no such algorithm exists in the general case. This result is the combined work of Martin Davis
Martin Davis
Martin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
, Yuri Matiyasevich
Yuri Matiyasevich
Yuri Vladimirovich Matiyasevich, is a Russian mathematician and computer scientist. He is best known for his negative solution of Hilbert's tenth problem, presented in his doctoral thesis, at LOMI .- Biography :* In 1962-1963 studied at Saint Petersburg Lyceum 239...
, Hilary Putnam
Hilary Putnam
Hilary Whitehall Putnam is an American philosopher, mathematician and computer scientist, who has been a central figure in analytic philosophy since the 1960s, especially in philosophy of mind, philosophy of language, philosophy of mathematics, and philosophy of science...
and Julia Robinson
Julia Robinson
Julia Hall Bowman Robinson was an American mathematician best known for her work on decision problems and Hilbert's Tenth Problem.-Background and education:...
.
Formulation
The words "process" and "finite number of operations" have been taken to mean that Hilbert was asking for an algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
. The term "rational integer" simply refers to the integers, positive, negative or zero: 0, ±1, ±2, ... . So Hilbert was asking for a general algorithm to decide whether a given polynomial Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
with integer coefficients has a solution in integers. The answer to the problem is now known to be in the negative: no such general algorithm can exist. Although it is unlikely that Hilbert had conceived of such a possibility, before going on to list the problems, he did presciently remark:
"Occasionally it happens that we seek the solution under insufficient hypotheses
or in an incorrect sense, and for this reason do not succeed. The problem then arises: to show the impossibility of the solution under the given hypotheses or in the sense contemplated."
The work on the problem has been in terms of solutions in natural numbers rather than arbitrary integers. But it is easy to see that an algorithm in either case could be used to obtain one for the other. If one possessed an algorithm to determine solvability in natural numbers, it could be used to determine whether an equation in
 unknowns,
unknowns,
has an integer solution by applying the supposed algorithm to the 2n equations

Conversely, an algorithm to test for solvability in arbitrary integers could be used to test a given equation for solvability in natural numbers by applying that supposed algorithm to the equation obtained from the given equation by replacing each unknown by the sum of the squares of four new unknowns. This works because of Lagrange's four-square theorem
Lagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
, to the effect that every natural number can be written as the sum of four squares.
Diophantine sets
Sets of natural numbers, of pairs of natural numbers (or even of n-tuples of natural numbers) that have Diophantine definitions are called Diophantine setDiophantine set
In mathematics, a Diophantine equation is an equation of the form P=0 where P is a polynomial with integer coefficients...
s.
Diophantine definitions can be provided by simultaneous systems of equations as well as by individual equations because the system

is equivalent to the single equation

A recursively enumerable set
Recursively enumerable set
In computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
can be characterized as one for which there exists an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that will ultimately halt when a member of the set is provided as input, but may continue indefinitely when the input is a non member. It was the development of computability theory
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
(also known as recursion theory
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
) that provided a precise explication of the intutitive notion of algorithmic computability, thus making the notion of recursive enumerability perfectly rigorous. It is evident that Diophantine sets are recursively enumerable. This is because one can arrange all possible tuples of values of the unknowns in a sequence and then, for a given value of the parameter(s), test these tuples, one after another, to see whether they are solutions of the corresponding equation. The unsolvability of Hilbert's tenth problem is a consequence of the surprising fact that the
converse is true:
Every recursively enumerable set is Diophantine.
This result is variously known as Matiyasevich's theorem (because he provided the crucial step that completed the proof) and the MRDP theorem (for Yuri Matiyasevich
Yuri Matiyasevich
Yuri Vladimirovich Matiyasevich, is a Russian mathematician and computer scientist. He is best known for his negative solution of Hilbert's tenth problem, presented in his doctoral thesis, at LOMI .- Biography :* In 1962-1963 studied at Saint Petersburg Lyceum 239...
, Julia Robinson
Julia Robinson
Julia Hall Bowman Robinson was an American mathematician best known for her work on decision problems and Hilbert's Tenth Problem.-Background and education:...
, Martin Davis
Martin Davis
Martin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
, and Hilary Putnam
Hilary Putnam
Hilary Whitehall Putnam is an American philosopher, mathematician and computer scientist, who has been a central figure in analytic philosophy since the 1960s, especially in philosophy of mind, philosophy of language, philosophy of mathematics, and philosophy of science...
). Because there exists a recursively enumerable set that is not computable, the unsolvability of Hilbert's tenth problem is an immediate consequence. In fact, more can be said: there is a polynomial

with integer coefficients such that the set of values of
 for which the equation
for which the equation
has solutions in natural numbers is not computable. So, not only is there no general algorithm for testing Diophantine equations for solvability, even for this one parameter family of equations, there is no algorithm.
History
| Year | Events |
|---|---|
| 1944 | Emil Leon Post Emil Leon Post Emil Leon Post was a mathematician and logician. He is best known for his work in the field that eventually became known as computability theory.-Early work:... declares that Hilbert's tenth problem "begs for an unsolvability proof". |
| 1949 | Martin Davis uses Kurt Gödel Kurt Gödel Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the... 's method for applying the Chinese Remainder Theorem Chinese remainder theorem The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers... as a coding trick to obtain his normal form for recursively enumerable sets: 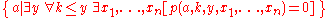 where 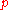 is a polynomial with integer coefficients. Purely formally, it is only the bounded universal quantifier that stands in the way of this being a Diophantine definition. is a polynomial with integer coefficients. Purely formally, it is only the bounded universal quantifier that stands in the way of this being a Diophantine definition.Using a non-constructive but easy proof, he notes that there is a Diophantine set whose complement is not Diophantine. Because the recursively enumerable sets also are not closed under complementation, he conjectures that the two classes are identical. |
| 1950 | Julia Robinson Julia Robinson Julia Hall Bowman Robinson was an American mathematician best known for her work on decision problems and Hilbert's Tenth Problem.-Background and education:... , unaware of Davis's work, but grasping the key importance of the exponential function, attempts to prove that EXP, the set of triplets 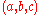 for which for which 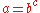 is Diophantine. Not succeeding, she is led to her hypothesis (later called J.R.): There is a Diophantine set  of pairs of pairs 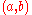 such that such that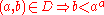 but for every  , ,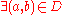 such that such that 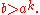 Using properties of the Pell equation, she proves that J.R. implies that EXP is Diophantine. Finally she shows, that if EXP is Diophantine so are the binomial coefficients, the factorial, and the primes. |
| 1959 | Working together, Davis and Putnam study exponential Diophantine sets: sets definable by Diophantine equations in which some of the exponents may be unknowns. Using the Davis normal form together with Robinson's methods, but assuming the then unproved conjecture that there are arbitrarily long arithmetic progressions consisting of prime numbers, they prove that every recursively enumerable set is exponential Diophantine, and as a consequence, that J.R. implies that every recursively enumerable set is Diophantine, and that Hilbert's tenth problem is unsolvable. |
| 1960 | Robinson shows how to avoid the unproved conjecture about primes in arithmetic progression and then greatly simplifies the proof. J.R. is revealed as the key to further progress, though many doubt that it is true. |
| 1961–1969 | Davis and Putnam find various propositions that imply J.R. Yuri Matiyasevich Yuri Matiyasevich Yuri Vladimirovich Matiyasevich, is a Russian mathematician and computer scientist. He is best known for his negative solution of Hilbert's tenth problem, presented in his doctoral thesis, at LOMI .- Biography :* In 1962-1963 studied at Saint Petersburg Lyceum 239... publishes some reductions of Hilbert's tenth problem. Robinson shows that the existence of an infinite Diophantine set of primes would suffice to establish J.R. |
| 1970 | Matiyasevich Yuri Matiyasevich Yuri Vladimirovich Matiyasevich, is a Russian mathematician and computer scientist. He is best known for his negative solution of Hilbert's tenth problem, presented in his doctoral thesis, at LOMI .- Biography :* In 1962-1963 studied at Saint Petersburg Lyceum 239... exhibits a system of 10 simultaneous first and second degree equations which provide a Diophantine definition of the set of pairs 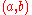 such that such that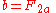 where where  is the nth Fibonacci number is the nth Fibonacci numberFibonacci number In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; .... . This proves J.R. and thus completes the proof that all recursively enumerable sets are Diophantine, and that therefore Hilbert's tenth problem is unsolvable. |
Applications
The Matiyasevich/MRDP Theorem relates two notions — one from computability theory, the other from number theory — and has some surprising consequences. Perhaps the most surprising is the existence of a universal Diophantine equation:- There exists a polynomial
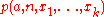 such that, given any Diophantine set
such that, given any Diophantine set 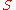 there is a number
there is a number  such that
such that
This can be seen to be true simply because there are universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
s, capable of executing any algorithm. This implication of J.R. had made it seem implausible.
Hilary Putnam has pointed out that for any Diophantine set
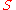 of positive integers, there is a polynomial
of positive integers, there is a polynomial
such that
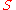 consists of exactly the positive numbers among the values assumed by
consists of exactly the positive numbers among the values assumed by 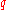 as
asthe variables

range over all natural numbers. This can be seen as follows: If

provides a Diophantine definition of
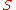 , then it suffices to set
, then it suffices to set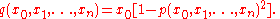
So, for example, there is a polynomial for which the positive part of its range is exactly the prime numbers. (On the other hand no polynomial can only take on prime values.)
Other applications concern what logicians refer to as
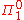 propositions, sometimes also called propositions of Goldbach type. These are like the Goldbach Conjecture, in stating that all natural numbers possess a certain property that is algorithmically checkable for each particular number. The Matiyasevich/MRDP Theorem implies that each such proposition is equivalent to a statement that asserts that some particular Diophantine equation has no solutions in natural numbers. A number of important and celebrated problems are of this form: in particular, Fermat's Last Theorem
propositions, sometimes also called propositions of Goldbach type. These are like the Goldbach Conjecture, in stating that all natural numbers possess a certain property that is algorithmically checkable for each particular number. The Matiyasevich/MRDP Theorem implies that each such proposition is equivalent to a statement that asserts that some particular Diophantine equation has no solutions in natural numbers. A number of important and celebrated problems are of this form: in particular, Fermat's Last TheoremFermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
, the Riemann Hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
, and the Four Color Theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
. In addition the assertion that particular formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
s such as Peano Arithmetic or ZFC are consistent can be expressed as
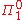 sentences. The idea is to follow Kurt Gödel
sentences. The idea is to follow Kurt GödelKurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
in coding proofs by natural numbers in such a way that the property of being the number representing a proof is algorithmically checkable.
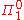 sentences have the special property that if they are false, that fact will be provable in any of the usual formal systems. This is because the falsity amounts to the existence of a counter-example which can be verified by simple arithmetic. So if a
sentences have the special property that if they are false, that fact will be provable in any of the usual formal systems. This is because the falsity amounts to the existence of a counter-example which can be verified by simple arithmetic. So if a 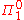 sentence is such that neither it nor its negation is provable in one of these systems, that sentence must be true.
sentence is such that neither it nor its negation is provable in one of these systems, that sentence must be true.A particularly striking form of Gödel's incompleteness theorem is also a consequence of the Matiyasevich/MRDP Theorem:
Let

provide a Diophantine definition of a non-computable set. Let
 be an algorithm that outputs a sequence of natural numbers
be an algorithm that outputs a sequence of natural numbers  such that the corresponding equation
such that the corresponding equation
has no solutions in natural numbers. Then there is a number
 which is not output by
which is not output by  while in fact the equation
while in fact the equation
has no solutions in natural numbers.
To see that the theorem is true, it suffices to notice that if there were no such number
 , one could algorithmically test membership of a number
, one could algorithmically test membership of a number  in this non-computable set by simultaneously running the algorithm
in this non-computable set by simultaneously running the algorithm  to see whether
to see whether  is output while also checking all possible
is output while also checking all possible 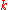 -tuples of natural numbers seeking a solution of the equation
-tuples of natural numbers seeking a solution of the equation
We may associate an algorithm
 with any of the usual formal systems such as Peano Arithmetic or ZFC by letting it systematically generate consequences of the axioms and then output a number
with any of the usual formal systems such as Peano Arithmetic or ZFC by letting it systematically generate consequences of the axioms and then output a number  whenever a sentence of the form
whenever a sentence of the form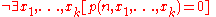
is generated. Then the theorem tells us that either a false statement of this form is proved or a true one remains unproved in the system in question.
Further results
We may speak of the degree of a Diophantine set as being the least degree of a polynomial in an equation defining that set. Similarly, we can call the dimension of such a set the least number of unknowns in a defining equation. Because of the existence of a universal Diophantine equation, it is clear that there are absolute upper bounds to both of these quantities, and there has been much interest in determining these bounds.Already in the 1920s Thoralf Skolem
Thoralf Skolem
Thoralf Albert Skolem was a Norwegian mathematician known mainly for his work on mathematical logic and set theory.-Life:...
showed that any Diophantine equation is equivalent to one of degree 4 or less. His trick was to introduce new unknowns by equations setting them equal to the square of an unknown or the product of two unknowns. Repetition of this process results in a system of second degree equations; then an equation of degree 4 is obtained by summing the squares. So every Diophantine set is trivially of degree 4 or less. It is not known whether this result is best possible.
Julia Robinson and Yuri Matiyasevich showed that every Diophantine set has dimension no greater than 13. Later, Matiyasevich sharpened their methods to show that 9 unknowns suffice. Although no one imagines that this striking result is the best possible, there has been no further progress. So, in particular, there is no algorithm for testing Diophantine equations with 9 or fewer unknowns for solvability in natural numbers. For the case of rational integer solutions (as Hilbert had originally posed it), the 4 squares trick shows that there is no algorithm for equations with no more than 36 unknowns. But Zhi Wei Sun showed that the problem for integers is unsolvable even for equations with no more than 11 unknowns.
Martin Davis studied algorithmic questions involving the number of solutions of a Diophantine equation. Hilbert's tenth problem asks whether or not that number is 0. Let
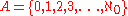 and let
and let  be a proper non-empty subset of
be a proper non-empty subset of  . Davis proved that there is no algorithm to test a given Diophantine equation to determine whether the number of its solutions is a member of the set
. Davis proved that there is no algorithm to test a given Diophantine equation to determine whether the number of its solutions is a member of the set  . Thus there is no algorithm to determine whether the number of solutions of a Diophantine equation
. Thus there is no algorithm to determine whether the number of solutions of a Diophantine equationis finite, odd, a perfect square, a prime, etc.
Extensions of Hilbert's tenth problem
Although Hilbert posed the problem for the rational integers, it can be just as well asked for many ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s (in particular, for any ring whose elements are listable). Obvious examples are the rings of integers of algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
s as well as the rational numbers. An algorithm such as he was requesting could have been extended to cover these other domains. For example, the equation
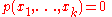
where
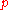 is a polynomial of degree
is a polynomial of degree 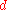 is solvable in non-negative rational numbers if and only if
is solvable in non-negative rational numbers if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
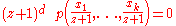
is solvable in natural numbers. (If one possessed an algorithm to determine solvability in non-negative rational numbers, it could easily be used to determine solvability in the rationals.) However, knowing that there is no such algorithm as Hilbert had desired says nothing about these other domains.
There has been much work on Hilbert's tenth problem for the rings of integers of algebraic number fields. Basing themselves on earlier work by Jan Denef
Jan Denef
Jan Denef is a Belgian mathematician. He is Full Professor of Mathematics at the Katholieke Universiteit Leuven.He is a specialist of model theory, number theory and algebraic geometry. He is well known for his early work on Hilbert's tenth problemand for developing the theory of motivic...
and Leonard Lipschitz and using class field theory, Harold N. Shapiro and Alexandra Shlapentokh were able to prove:
Hilbert's tenth problem is unsolvable for the ring of integers of any algebraic number field whose Galois group over the rationals is abelian.
Shlapentokh and Thanases Pheidas (independently of one another) obtained the same result for algebraic number fields admitting exactly one pair of complex conjugate embeddings.
The problem for the ring of integers of algebraic number fields other than those covered by the results above remains open. Likewise, despite much interest, the problem for equations over the rationals remains open. Barry Mazur
Barry Mazur
-Life:Born in New York City, Mazur attended the Bronx High School of Science and MIT, although he did not graduate from the latter on account of failing a then-present ROTC requirement. Regardless, he was accepted for graduate school and received his Ph.D. from Princeton University in 1959,...
has conjectured that for any variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
over the rationals, the topological closure over the reals of the set of solutions has only finitely many components. This conjecture implies that the integers are not Diophantine over the rationals and so if this conjecture is true a negative answer to Hilbert's Tenth Problem would require a different approach than that used for other rings.