A self-complementary graph is a graph

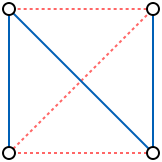
Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

 which is isomorphic

Graph isomorphism

In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...

 to its complement. The simplest non-trivial self-complementary graphs are the 4-vertex path graph

Path graph

In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...

 and the 5-vertex cycle graph

Cycle graph

In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...

.

Self-complementary graphs are interesting in their relation to the graph isomorphism problem

Graph isomorphism problem

The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.Besides its practical importance, the graph isomorphism problem is a curiosity in computational complexity theory as it is one of a very small number of problems belonging to NP...

: the problems of checking whether two self-complementary graphs are isomorphic and of checking whether a given graph is self-complementary are polynomial-time equivalent to the general graph isomorphism problem.

An n-vertex self-complementary graph has exactly half number of edges of the complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

, i.e., n(n − 1)/4 edges, and (if there is more than one vertex) it must have diameter either 2 or 3. Since n(n −1) must be divisible by 4, n must be congruent

Congruence relation

In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...

 to 0 or 1 mod 4; for instance, a 6-vertex graph cannot be self-complementary.

Every Paley graph

Paley graph

In mathematics, and specifically graph theory, Paley graphs, named after Raymond Paley, are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ in a quadratic residue. The Paley graphs form an infinite family of conference...

 is self-complementary. All strongly regular

Strongly regular graph

In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...

 self-complementary graphs with fewer than 37 vertices are Paley graphs; however, there are strongly regular graphs on 37, 41, and 49 vertices that are not Paley graphs.

The Rado graph

Rado graph

In the mathematical field of graph theory, the Rado graph, also known as the random graph or the Erdős–Renyi graph, is the unique countable graph R such that for any finite graph G and any vertex v of G, any embedding of G − v as an induced subgraph of R can be extended to an...

is an infinite self-complementary graph.