
Generalized Verma module
Encyclopedia
In mathematics
, generalized Verma modules are a generalization of a (true) Verma module
, and are objects in the representation theory
of Lie algebras. They were studied originally by James Lepowsky
in the nineteen seventies. The motivation for their study is that their homomorphisms correspond to invariant differential operators over generalized flag manifolds. The study of these operators is an important part of the theory of parabolic geometries.
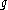 be a semisimple Lie algebra and
be a semisimple Lie algebra and 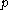 a parabolic subalgebra of
a parabolic subalgebra of 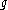 . For any irreducible finite dimensional representation
. For any irreducible finite dimensional representation
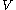 of
of 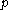 we define the generalized Verma module to be the relative tensor product
we define the generalized Verma module to be the relative tensor product
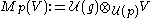 .
.
The action of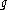 is left multiplication in
is left multiplication in 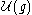 .
.
If λ is the highest weight of V, we sometimes denote the Verma module by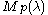 .
.
Note that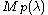 makes sense only for
makes sense only for 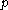 -dominant and
-dominant and 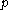 -integral weights (see weight
-integral weights (see weight
)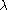 .
.
It is well known that a parabolic subalgebra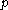 of
of 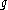 determines a unique grading
determines a unique grading
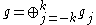 so that
so that 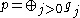 .
.
Let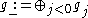 .
.
It follows from the Poincaré-Birkhoff-Witt theorem that, as a vector space (and even as a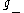 -module
-module
and as a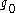 -module),
-module),
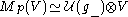 .
.
In further text, we will denote a generalized Verma module simply by GVM.
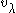 is the highest weight vector in V, then
is the highest weight vector in V, then 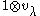 is the highest weight vector in
is the highest weight vector in 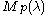 .
.
GVM's are weight modules, i.e. they are direct sum of its weight spaces and these weight spaces are finite dimensional.
As all highest weight modules, GVM's are quotients of Verma modules. The kernel
of the projection
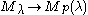 is
is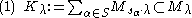
where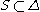 is the set of those simple root
is the set of those simple root
s α such that the negative root spaces of root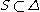 are in
are in 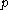 (the set S determines uniquely the subalgebra
(the set S determines uniquely the subalgebra 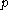 ),
), 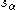 is the root reflection with respect to the root α and
is the root reflection with respect to the root α and
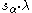 is the affine action of
is the affine action of 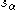 on λ. It follows from the theory of (true) Verma module
on λ. It follows from the theory of (true) Verma module
s that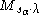 is isomorphic to a unique submodule of
is isomorphic to a unique submodule of 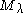 . In (1), we identified
. In (1), we identified 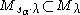 . The sum in (1) is not direct
. The sum in (1) is not direct
.
In the special case when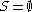 , the parabolic subalgebra
, the parabolic subalgebra 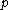 is the Borel subalgebra and the GVM coincides with (true) Verma module. In the other extremal case when
is the Borel subalgebra and the GVM coincides with (true) Verma module. In the other extremal case when 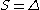 ,
, 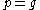 and the GVM is isomorphic to the inducing representation V.
and the GVM is isomorphic to the inducing representation V.
The GVM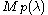 is called regular, if its highest weight λ is on the affine Weyl orbit of a dominant weight
is called regular, if its highest weight λ is on the affine Weyl orbit of a dominant weight 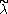 . In other word, there exist an element w of the Weyl group W such that
. In other word, there exist an element w of the Weyl group W such that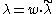
where is the affine action of the Weyl group.
is the affine action of the Weyl group.
The Verma module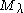 is called singular, if there is no dominant weight on the affine orbit of λ. In this case, there exists a weight
is called singular, if there is no dominant weight on the affine orbit of λ. In this case, there exists a weight 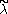 so that
so that 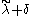 is on the wall of the fundamental Weyl chamber (δ is the sum of all fundamental weights).
is on the wall of the fundamental Weyl chamber (δ is the sum of all fundamental weights).
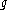 -homomorphism.
-homomorphism.
For any two weights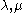 a homomorphism
a homomorphism
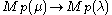
may exist only if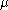 and
and 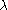 are linked with an affine action of the Weyl group
are linked with an affine action of the Weyl group
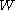 of the Lie algebra
of the Lie algebra 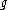 . This follows easily from the Harish-Chandra theorem
. This follows easily from the Harish-Chandra theorem
on infinitesimal central characters.
Unlike in the case of (true) Verma module
s, the homomorphisms of GVM's are in general not injective and the dimension
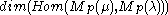
may be larger than one in some specific cases.
If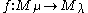 is a homomorphism of (true) Verma modules,
is a homomorphism of (true) Verma modules, 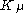 resp.
resp. 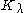 is the kernels of the projection
is the kernels of the projection 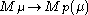 , resp.
, resp. 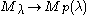 , then there exists a homomorphism
, then there exists a homomorphism 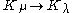 and f factors to a homomorphism of generalized Verma modules
and f factors to a homomorphism of generalized Verma modules 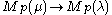 . Such a homomorphism (that is a factor of a homomorphism of Verma modules) is called standard. However, the standard homomorphism may be zero in some cases.
. Such a homomorphism (that is a factor of a homomorphism of Verma modules) is called standard. However, the standard homomorphism may be zero in some cases.
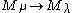 .
.
Let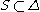 be the set of those simple root
be the set of those simple root
s α such that the negative root spaces of root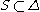 are in
are in 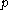 (like in section Properties).
(like in section Properties).
The following theorem is proved by Lepowsky
:
The structure of GVM's on the affine orbit of a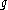 -dominant and
-dominant and 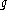 -integral weight
-integral weight
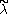 can be described explicitly. If W is the Weyl group
can be described explicitly. If W is the Weyl group
of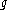 , there exists a subset
, there exists a subset 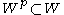 of such elements, so that
of such elements, so that 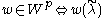 is
is 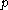 -dominant. It can be shown that
-dominant. It can be shown that 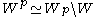 where
where 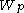 is the Weyl group
is the Weyl group
of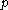 (in particular,
(in particular, 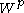 does not depend on the choice of
does not depend on the choice of 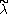 ). The map
). The map 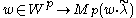 is a bijection between
is a bijection between 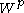 and the set of GVM's with highest weights on the affine orbit of
and the set of GVM's with highest weights on the affine orbit of 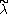 . Let as suppose that
. Let as suppose that 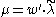 ,
, 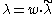 and
and 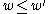 in the Bruhat ordering (otherwise, there is no homomorphism of (true) Verma modules
in the Bruhat ordering (otherwise, there is no homomorphism of (true) Verma modules 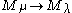 and the standard homomorphism does not make sense, see Homomorphisms of Verma modules).
and the standard homomorphism does not make sense, see Homomorphisms of Verma modules).
The following statements follow from the above theorem and the structure of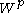 :
:
However, if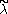 is only dominant but not integral, there may stil exist
is only dominant but not integral, there may stil exist 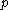 -dominant and
-dominant and 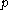 -integral weights on its affine orbit.
-integral weights on its affine orbit.
The situation is even more complicated if the GVM's have singular character, i.e. there and
and  are on the affine orbit of some
are on the affine orbit of some  such that
such that  is on the wall of the fundamental Weyl chamber.
is on the wall of the fundamental Weyl chamber.
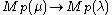 is called nonstandard, if it is not standard. It may happen that the standard homomorphism of GVM's is zero but there stil exists a nonstandard homomorphism.
is called nonstandard, if it is not standard. It may happen that the standard homomorphism of GVM's is zero but there stil exists a nonstandard homomorphism.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, generalized Verma modules are a generalization of a (true) Verma module
Verma module
Verma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties...
, and are objects in the representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of Lie algebras. They were studied originally by James Lepowsky
James Lepowsky
James Lepowsky is a professor of mathematics at Rutgers University, New Jersey. Previously he taught at Yale University. He received his Ph.D from M.I.T. in 1970 where his advisor was Bertram Kostant. Lepowsky graduated from Stuyvesant High School in 1961, 16 years after Kostant...
in the nineteen seventies. The motivation for their study is that their homomorphisms correspond to invariant differential operators over generalized flag manifolds. The study of these operators is an important part of the theory of parabolic geometries.
Definition
Let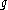 be a semisimple Lie algebra and
be a semisimple Lie algebra and 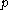 a parabolic subalgebra of
a parabolic subalgebra of 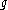 . For any irreducible finite dimensional representation
. For any irreducible finite dimensional representationRepresentation of a Lie algebra
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
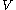 of
of 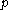 we define the generalized Verma module to be the relative tensor product
we define the generalized Verma module to be the relative tensor product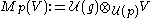 .
.The action of
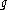 is left multiplication in
is left multiplication in 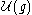 .
.If λ is the highest weight of V, we sometimes denote the Verma module by
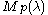 .
.Note that
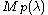 makes sense only for
makes sense only for 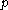 -dominant and
-dominant and 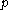 -integral weights (see weight
-integral weights (see weightWeight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
)
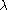 .
.It is well known that a parabolic subalgebra
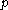 of
of 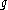 determines a unique grading
determines a unique gradingGraded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
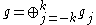 so that
so that 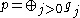 .
.Let
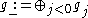 .
.It follows from the Poincaré-Birkhoff-Witt theorem that, as a vector space (and even as a
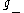 -module
-moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
and as a
 -module),
-module), .
.In further text, we will denote a generalized Verma module simply by GVM.
Properties of GVM's
GVM's are highest weight modules and their highest weight λ is the highest weight of the representation V. If is the highest weight vector in V, then
is the highest weight vector in V, then  is the highest weight vector in
is the highest weight vector in 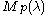 .
.GVM's are weight modules, i.e. they are direct sum of its weight spaces and these weight spaces are finite dimensional.
As all highest weight modules, GVM's are quotients of Verma modules. The kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of the projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
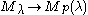 is
is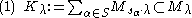
where
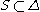 is the set of those simple root
is the set of those simple rootSimple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s α such that the negative root spaces of root
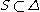 are in
are in 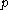 (the set S determines uniquely the subalgebra
(the set S determines uniquely the subalgebra 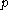 ),
), 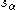 is the root reflection with respect to the root α and
is the root reflection with respect to the root α and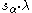 is the affine action of
is the affine action of 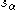 on λ. It follows from the theory of (true) Verma module
on λ. It follows from the theory of (true) Verma moduleVerma module
Verma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties...
s that
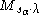 is isomorphic to a unique submodule of
is isomorphic to a unique submodule of 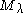 . In (1), we identified
. In (1), we identified 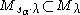 . The sum in (1) is not direct
. The sum in (1) is not directDirect sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
.
In the special case when
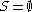 , the parabolic subalgebra
, the parabolic subalgebra 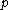 is the Borel subalgebra and the GVM coincides with (true) Verma module. In the other extremal case when
is the Borel subalgebra and the GVM coincides with (true) Verma module. In the other extremal case when 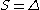 ,
, 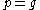 and the GVM is isomorphic to the inducing representation V.
and the GVM is isomorphic to the inducing representation V.The GVM
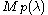 is called regular, if its highest weight λ is on the affine Weyl orbit of a dominant weight
is called regular, if its highest weight λ is on the affine Weyl orbit of a dominant weight 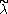 . In other word, there exist an element w of the Weyl group W such that
. In other word, there exist an element w of the Weyl group W such that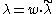
where
 is the affine action of the Weyl group.
is the affine action of the Weyl group.The Verma module
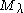 is called singular, if there is no dominant weight on the affine orbit of λ. In this case, there exists a weight
is called singular, if there is no dominant weight on the affine orbit of λ. In this case, there exists a weight 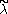 so that
so that 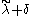 is on the wall of the fundamental Weyl chamber (δ is the sum of all fundamental weights).
is on the wall of the fundamental Weyl chamber (δ is the sum of all fundamental weights).Homomorphisms of GVM's
By a homomorphism of GVM's we mean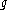 -homomorphism.
-homomorphism.For any two weights
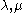 a homomorphism
a homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
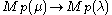
may exist only if
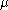 and
and 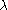 are linked with an affine action of the Weyl group
are linked with an affine action of the Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
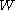 of the Lie algebra
of the Lie algebra 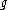 . This follows easily from the Harish-Chandra theorem
. This follows easily from the Harish-Chandra theoremHarish-Chandra theorem
In matheamtics, Harish-Chandra theorem may refer to one of several theorems due to Harish-Chandra,including:*Harish-Chandra's theorem on the Harish-Chandra isomorphism*Harish-Chandra's classification of discrete series representations...
on infinitesimal central characters.
Unlike in the case of (true) Verma module
Verma module
Verma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties...
s, the homomorphisms of GVM's are in general not injective and the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
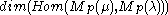
may be larger than one in some specific cases.
If
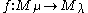 is a homomorphism of (true) Verma modules,
is a homomorphism of (true) Verma modules, 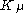 resp.
resp. 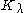 is the kernels of the projection
is the kernels of the projection 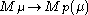 , resp.
, resp. 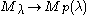 , then there exists a homomorphism
, then there exists a homomorphism 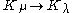 and f factors to a homomorphism of generalized Verma modules
and f factors to a homomorphism of generalized Verma modules 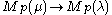 . Such a homomorphism (that is a factor of a homomorphism of Verma modules) is called standard. However, the standard homomorphism may be zero in some cases.
. Such a homomorphism (that is a factor of a homomorphism of Verma modules) is called standard. However, the standard homomorphism may be zero in some cases.Standard
Let us suppose that there exists a nontrivial homomorphism of true Verma moduls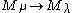 .
.Let
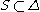 be the set of those simple root
be the set of those simple rootSimple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s α such that the negative root spaces of root
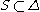 are in
are in 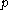 (like in section Properties).
(like in section Properties).The following theorem is proved by Lepowsky
James Lepowsky
James Lepowsky is a professor of mathematics at Rutgers University, New Jersey. Previously he taught at Yale University. He received his Ph.D from M.I.T. in 1970 where his advisor was Bertram Kostant. Lepowsky graduated from Stuyvesant High School in 1961, 16 years after Kostant...
:
The standard homomorphismis zero if and only if there exists
such that
is isomorphic to a submodule of
(
is the corresponding root reflection and
is the affine action).
The structure of GVM's on the affine orbit of a
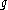 -dominant and
-dominant and 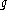 -integral weight
-integral weightWeight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
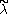 can be described explicitly. If W is the Weyl group
can be described explicitly. If W is the Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of
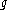 , there exists a subset
, there exists a subset 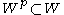 of such elements, so that
of such elements, so that 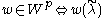 is
is 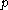 -dominant. It can be shown that
-dominant. It can be shown that 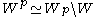 where
where 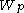 is the Weyl group
is the Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of
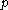 (in particular,
(in particular, 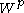 does not depend on the choice of
does not depend on the choice of 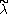 ). The map
). The map 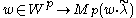 is a bijection between
is a bijection between 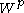 and the set of GVM's with highest weights on the affine orbit of
and the set of GVM's with highest weights on the affine orbit of 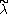 . Let as suppose that
. Let as suppose that 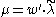 ,
, 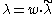 and
and 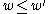 in the Bruhat ordering (otherwise, there is no homomorphism of (true) Verma modules
in the Bruhat ordering (otherwise, there is no homomorphism of (true) Verma modules 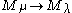 and the standard homomorphism does not make sense, see Homomorphisms of Verma modules).
and the standard homomorphism does not make sense, see Homomorphisms of Verma modules).The following statements follow from the above theorem and the structure of
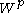 :
:
Theorem. Iffor some positive root
and the length (see Bruhat ordering) l(w')=l(w)+1, then there exists a nonzero standard homomorphism
.
Theorem. The standard homomorphismis zero if and only if there exists
such that
and
.
However, if
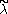 is only dominant but not integral, there may stil exist
is only dominant but not integral, there may stil exist 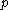 -dominant and
-dominant and 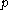 -integral weights on its affine orbit.
-integral weights on its affine orbit.The situation is even more complicated if the GVM's have singular character, i.e. there
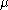 and
and 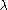 are on the affine orbit of some
are on the affine orbit of some 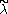 such that
such that 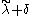 is on the wall of the fundamental Weyl chamber.
is on the wall of the fundamental Weyl chamber.Nonstandard
A homomorphism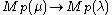 is called nonstandard, if it is not standard. It may happen that the standard homomorphism of GVM's is zero but there stil exists a nonstandard homomorphism.
is called nonstandard, if it is not standard. It may happen that the standard homomorphism of GVM's is zero but there stil exists a nonstandard homomorphism.

