Galton-Watson process
Encyclopedia
The Galton–Watson process is a branching
stochastic process
arising from Francis Galton
's statistical investigation of the extinction of family name
s.
There was concern amongst the Victorian
s that aristocratic
surnames were becoming extinct. Galton originally posed the question regarding the probability of such an event in the Educational Times of 1873, and the Reverend Henry William Watson
replied with a solution. Together, they then wrote an 1874 paper entitled On the probability of extinction of families. Galton and Watson appear to have derived their process independently of the earlier work by I. J. Bienaymé
; see Heyde and Seneta 1977. For a detailed history see Kendall (1966 and 1975).
distributed
on the set { 0, 1, 2, 3, ... }. Further suppose the numbers of different men's sons to be independent
random variables, all having the same distribution.
Then the simplest substantial mathematical conclusion is that if the average number of a man's sons is 1 or less, then their surname will almost surely
die out, and if it is more than 1, then there is more than zero probability that it will survive for any given number of generations.
Modern applications include the survival probabilities for a new mutant
gene, or the initiation of a nuclear chain reaction
, or the dynamics of disease outbreak
s in their first generations of spread, or the chances of extinction
of small population
of organism
s; as well as explaining (perhaps closest to Galton's original interest) why only a handful of males in the deep past of humanity now have any surviving male-line descendants, reflected in a rather small number of distinctive human Y-chromosome DNA haplogroups
.
A corollary of high extinction probabilities is that if a lineage has survived, it is likely to have experienced, purely by chance, an unusually high growth rate in its early generations at least when compared to the rest of the population.
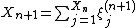
where for each n,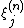
is a sequence of IID natural number-valued random variables. The extinction probability (i.e. the probability of final extinction) is given by
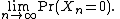
This is clearly equal to zero if each member of the population has exactly one descendent. Excluding this case (usually called the trivial case) there exists
a simple necessary and sufficient condition, which is given in the next section.
The process can be treated analytically using the method of probability generating functions.
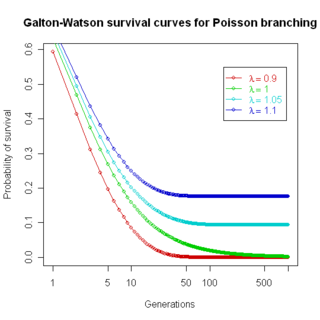
If the number of children ξ j at each node follows a Poisson distribution
, a particularly simple recurrence can be found for the total extinction probability xn for a process starting with a single individual at time n = 0:
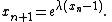
giving the curves plotted above.
.) In this process, each child is supposed as male or female, independently of each other, with a specified probability, and a so-called 'mating function' determines how many couples will form in a given generation. As before, reproduction of different couples are considered to be independent of each other. Now the analogue of the trivial case corresponds to the case of each male and female reproducing in exactly one couple, having one male and one female descendent, and that the mating function takes the value of the minimum of the number of males and females (which are then the same from the next generation onwards).
Since the total reproduction within a generation depends now strongly on the mating function, there exists in general no simple necessary and sufficient condition for final extinction as it is the case in the classical Galton–Watson process. However, excluding the non-trivial case, the concept of the averaged reproduction mean (Bruss (1984)) allows for a general sufficient condition for final extinction, treated in the next section.
evidence for names having become extinct over time, or that they did so due to dying out of family name lines – that requires that there were more names in the past and that they die out due to the line dying out, rather than the name changing for other reasons, such as vassals assuming the name of their lord.
Chinese names are a well-studied example of surname extinction: there are currently only about 3,100 surnames in use in China, compared with close to 12,000 recorded in the past, with 22% of the population sharing three family names (numbering close to 300 million people), and the top 200 names covering 96% of the population. While the surname extinction is partly due to family name lines dying out, names also changed historically for other reasons, such as people taking the names of their rulers. Indeed, the most significant factor affecting the surname frequency is other ethnic groups identifying as Han and adopting Han names. Further, while new names have arisen for various reasons, this has been outweighed by old names disappearing.
By contrast, some nations have adopted family names only recently. This means both that they have not experienced surname extinction for an extended period, and that the names were adopted when the nation had a relatively large population, rather than the smaller populations of ancient times. Further, these names have often been chosen creatively and are very diverse. Examples include:
On the other hand, some examples of high concentration of family names is not primarily due to the Galton–Watson process:
Branching process
In probability theory, a branching process is a Markov process that models a population in which each individual in generation n produces some random number of individuals in generation n + 1, according to a fixed probability distribution that does not vary from individual to...
stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
arising from Francis Galton
Francis Galton
Sir Francis Galton /ˈfrɑːnsɪs ˈgɔːltn̩/ FRS , cousin of Douglas Strutt Galton, half-cousin of Charles Darwin, was an English Victorian polymath: anthropologist, eugenicist, tropical explorer, geographer, inventor, meteorologist, proto-geneticist, psychometrician, and statistician...
's statistical investigation of the extinction of family name
Family name
A family name is a type of surname and part of a person's name indicating the family to which the person belongs. The use of family names is widespread in cultures around the world...
s.
Victorian era
The Victorian era of British history was the period of Queen Victoria's reign from 20 June 1837 until her death on 22 January 1901. It was a long period of peace, prosperity, refined sensibilities and national self-confidence...
s that aristocratic
Aristocracy (class)
The aristocracy are people considered to be in the highest social class in a society which has or once had a political system of Aristocracy. Aristocrats possess hereditary titles granted by a monarch, which once granted them feudal or legal privileges, or deriving, as in Ancient Greece and India,...
surnames were becoming extinct. Galton originally posed the question regarding the probability of such an event in the Educational Times of 1873, and the Reverend Henry William Watson
Henry William Watson
Rev. Henry William Watson was a noted mathematician and author of a number of mathematics books....
replied with a solution. Together, they then wrote an 1874 paper entitled On the probability of extinction of families. Galton and Watson appear to have derived their process independently of the earlier work by I. J. Bienaymé
Irénée-Jules Bienaymé
Irénée-Jules Bienaymé , was a French statistician. He built on the legacy of Laplace generalizing his least squares method. He contributed to the fields and probability, and statistics and to their application to finance, demography and social sciences...
; see Heyde and Seneta 1977. For a detailed history see Kendall (1966 and 1975).
Concepts
Assume, as was taken for granted in Galton's time, that surnames are passed on to all male children by their father. Suppose the number of a man's sons to be a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
distributed
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
on the set { 0, 1, 2, 3, ... }. Further suppose the numbers of different men's sons to be independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variables, all having the same distribution.
Then the simplest substantial mathematical conclusion is that if the average number of a man's sons is 1 or less, then their surname will almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
die out, and if it is more than 1, then there is more than zero probability that it will survive for any given number of generations.
Modern applications include the survival probabilities for a new mutant
Mutant
In biology and especially genetics, a mutant is an individual, organism, or new genetic character, arising or resulting from an instance of mutation, which is a base-pair sequence change within the DNA of a gene or chromosome of an organism resulting in the creation of a new character or trait not...
gene, or the initiation of a nuclear chain reaction
Nuclear chain reaction
A nuclear chain reaction occurs when one nuclear reaction causes an average of one or more nuclear reactions, thus leading to a self-propagating number of these reactions. The specific nuclear reaction may be the fission of heavy isotopes or the fusion of light isotopes...
, or the dynamics of disease outbreak
Epidemic
In epidemiology, an epidemic , occurs when new cases of a certain disease, in a given human population, and during a given period, substantially exceed what is expected based on recent experience...
s in their first generations of spread, or the chances of extinction
Extinction
In biology and ecology, extinction is the end of an organism or of a group of organisms , normally a species. The moment of extinction is generally considered to be the death of the last individual of the species, although the capacity to breed and recover may have been lost before this point...
of small population
Population
A population is all the organisms that both belong to the same group or species and live in the same geographical area. The area that is used to define a sexual population is such that inter-breeding is possible between any pair within the area and more probable than cross-breeding with individuals...
of organism
Organism
In biology, an organism is any contiguous living system . In at least some form, all organisms are capable of response to stimuli, reproduction, growth and development, and maintenance of homoeostasis as a stable whole.An organism may either be unicellular or, as in the case of humans, comprise...
s; as well as explaining (perhaps closest to Galton's original interest) why only a handful of males in the deep past of humanity now have any surviving male-line descendants, reflected in a rather small number of distinctive human Y-chromosome DNA haplogroups
Human Y-chromosome DNA haplogroups
In human genetics, a Human Y-chromosome DNA haplogroup is a haplogroup defined by differences in the non-recombining portions of DNA from the Y chromosome ....
.
A corollary of high extinction probabilities is that if a lineage has survived, it is likely to have experienced, purely by chance, an unusually high growth rate in its early generations at least when compared to the rest of the population.
Mathematical definition
A Galton–Watson process is a stochastic process {Xn} which evolves according to the recurrence formula X0 = 1 and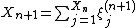where for each n,
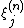is a sequence of IID natural number-valued random variables. The extinction probability (i.e. the probability of final extinction) is given by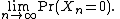This is clearly equal to zero if each member of the population has exactly one descendent. Excluding this case (usually called the trivial case) there exists
a simple necessary and sufficient condition, which is given in the next section.
Extinction criterion for Galton–Watson process
In the non-trivial case the probability of final extinction is equal to one if E{ξ1} ≤ 1 and strictly less than one if E{ξ1} > 1.The process can be treated analytically using the method of probability generating functions.
If the number of children ξ j at each node follows a Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
, a particularly simple recurrence can be found for the total extinction probability xn for a process starting with a single individual at time n = 0:
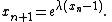
giving the curves plotted above.
Bisexual Galton–Watson process
In the classical Galton–Watson process described above, only men are considered, effectively modeling reproduction as asexual. A model more closely following actual sexual reproduction is the so-called 'bisexual Galton–Watson process', where only couples reproduce. (Bisexual in this context refers to the number of sexes involved, not sexual orientationSexual orientation
Sexual orientation describes a pattern of emotional, romantic, or sexual attractions to the opposite sex, the same sex, both, or neither, and the genders that accompany them. By the convention of organized researchers, these attractions are subsumed under heterosexuality, homosexuality,...
.) In this process, each child is supposed as male or female, independently of each other, with a specified probability, and a so-called 'mating function' determines how many couples will form in a given generation. As before, reproduction of different couples are considered to be independent of each other. Now the analogue of the trivial case corresponds to the case of each male and female reproducing in exactly one couple, having one male and one female descendent, and that the mating function takes the value of the minimum of the number of males and females (which are then the same from the next generation onwards).
Since the total reproduction within a generation depends now strongly on the mating function, there exists in general no simple necessary and sufficient condition for final extinction as it is the case in the classical Galton–Watson process. However, excluding the non-trivial case, the concept of the averaged reproduction mean (Bruss (1984)) allows for a general sufficient condition for final extinction, treated in the next section.
Extinction criterion (bisexual Galton–Watson process)
If in the non-trivial case the averaged reproduction mean per couple stays bounded over all generations and will not exceed 1 for a sufficiently large population size, then the probability of final extinction is always 1.Examples
Citing historical examples of Galton–Watson process is complicated due to the history of family names often deviating significantly from the theoretical model. Notably, new names can be created, existing names can be changed over a person's lifetime, and people historically have often assumed names of unrelated persons, particularly nobility. Thus, a small number of family names at present is not in itselfIpso facto
Ipso facto is a Latin phrase, directly translated as "by the fact itself," which means that a certain phenomenon is a direct consequence, a resultant effect, of the action in question, instead of being brought about by a subsequent action such as the verdict of a tribunal. It is a term of art used...
evidence for names having become extinct over time, or that they did so due to dying out of family name lines – that requires that there were more names in the past and that they die out due to the line dying out, rather than the name changing for other reasons, such as vassals assuming the name of their lord.
Chinese names are a well-studied example of surname extinction: there are currently only about 3,100 surnames in use in China, compared with close to 12,000 recorded in the past, with 22% of the population sharing three family names (numbering close to 300 million people), and the top 200 names covering 96% of the population. While the surname extinction is partly due to family name lines dying out, names also changed historically for other reasons, such as people taking the names of their rulers. Indeed, the most significant factor affecting the surname frequency is other ethnic groups identifying as Han and adopting Han names. Further, while new names have arisen for various reasons, this has been outweighed by old names disappearing.
By contrast, some nations have adopted family names only recently. This means both that they have not experienced surname extinction for an extended period, and that the names were adopted when the nation had a relatively large population, rather than the smaller populations of ancient times. Further, these names have often been chosen creatively and are very diverse. Examples include:
- Japanese names, which in general use date only to the Meiji restorationMeiji RestorationThe , also known as the Meiji Ishin, Revolution, Reform or Renewal, was a chain of events that restored imperial rule to Japan in 1868...
in the late 19th century (when the population was over 30,000,000), have over 100,000 family names, surnames are very varied, and the government restricts married couples to using the same surname. - Many Dutch nameDutch nameDutch names consist of one or more given names and a surname. The given name, as in English, is usually gender-specific.-Dutch given names:The given name is given to a child by the parents shortly after, or before, birth. It is common to give a child several given names, particularly among...
s have only included a family name since the Napoleonic WarsNapoleonic WarsThe Napoleonic Wars were a series of wars declared against Napoleon's French Empire by opposing coalitions that ran from 1803 to 1815. As a continuation of the wars sparked by the French Revolution of 1789, they revolutionised European armies and played out on an unprecedented scale, mainly due to...
in the early 19th century, and there are over 68,000 Dutch family names. - Thai nameThai nameThai names follow the North Indian and Western European pattern in which the family name follows a first or given name. In this they differ from the family-name-first pattern of the East Asian tradition....
s have only included a family name since 1920, and only a single family can use a given family name, hence there are a great number of Thai names. Further, Thai people change their family names with some frequency, complicating the analysis.
On the other hand, some examples of high concentration of family names is not primarily due to the Galton–Watson process:
- Vietnamese nameVietnamese nameVietnamese names generally consist of three parts: a family name, a middle name, and a given name, used in that order. The "family name first" order follows the system of Chinese names and is common throughout the Sinosphere , but is different from Chinese, Korean, and Japanese names in having a...
s have about 100 family names, and 60% of the population sharing three family names. The name Nguyễn alone is estimated to be used by almost 40% of the Vietnamese population, and 90% share 15 names. However, as the history of the Nguyễn name makes clear, this is in no small part due to names being forced on people or adopted for reasons unrelated to genetic relation. - Korean nameKorean nameA Korean name consists of a family name followed by a given name, as used by the Korean people in both North Korea and South Korea. In the Korean language, 'ireum' or 'seong-myeong' usually refers to the family name and given name together...
s are similarly concentrated, with 250 family names, and 45% of the population sharing three family names. However, as recently as 1910, over half the population did not have family names. The lack of diversity is thus not primarily due to the Galton–Watson process, but rather to family names, though recent, not being chosen creatively, but rather on the basis of existing names.