G-delta set
Encyclopedia
In the mathematical field of topology
, a Gδ set is a subset
of a topological space
that is a countable intersection of open sets. The notation originated in Germany
with G for Gebiet (German
: area, or neighborhood) meaning open set
in this case and δ for Durchschnitt (German: intersection
).
The term inner limiting set is also used. Gδ sets, and their dual Fσ sets
, are the second level of the Borel hierarchy
.
of open set
s. The Gδ sets are exactly the level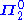
sets of the Borel hierarchy
.
A more elaborate example of a Gδ set is given by the following theorem:
Theorem: The set
is dense in 
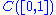and contains a Gδ subset of the metric space 
(and topological
) spaces is strongly related to the notion of completeness of the metric space as well as to the Baire category theorem
. This is described by the Mazurkiewicz
theorem:
Theorem (Mazurkiewicz
): Let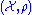
be a complete metric space and 
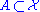. Then the following are equivalent:
A key property of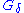
sets is that they are the possible sets at which a function from a topological space to a metric space is continuous
. Formally: The set of points where a function
is continuous is a 
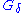set. This is because continuity at a point 
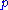can be defined by a 
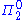formula, namely: For all positive integers 
, there is an open set 
containing 
such that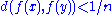 
for all 
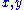in 
. If a value of 
is fixed, the set of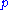 
for which there is such a corresponding open 
is itself an open set (being a union of open sets), and the universal quantifier on 
corresponds to the (countable) intersection of these sets. In the real line, the converse holds as well; for any Gδ subset A of the real line, there is a function f: R → R which is continuous exactly at the points in A. As a consequence, while it is possible for the irrationals to be the set of continuity points of a function (see the popcorn function
), it is impossible to construct a function which is continuous only on the rational numbers.
The following results regard Polish space
s:
is a Gδ set (Johnson, 1970). A normal space
which is also a Gδ space is perfectly normal. Every metrizable space is perfectly normal, and every perfectly normal space is completely normal: neither implication is reversible.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a Gδ set is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that is a countable intersection of open sets. The notation originated in Germany
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
with G for Gebiet (German
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
: area, or neighborhood) meaning open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in this case and δ for Durchschnitt (German: intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
).
The term inner limiting set is also used. Gδ sets, and their dual Fσ sets
F-sigma set
In mathematics, an Fσ set is a countable union of closed sets. The notation originated in France with F for fermé and σ for somme ....
, are the second level of the Borel hierarchy
Borel hierarchy
In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
.
Definition
In a topological space a Gδ set is a countable intersectionIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s. The Gδ sets are exactly the level
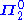sets of the Borel hierarchyBorel hierarchy
In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
.
Examples
- Any open set is trivially a Gδ set
- The irrational numbers are a Gδ set in R, the real numbers, as they can be written as the intersection over all rationalRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
numbers q of the complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of {q} in R. Note that the set of rationalRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
numbers is not a Gδ set in R.
- The rational numbers Q are not a Gδ set. If we were able to write Q as the intersection of open sets An, each An would have to be denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in R since Q is dense in R. However, the construction above gave the irrational numbers as a countable intersection of open dense subsets. Taking the intersection of both of these sets gives the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
as a countable intersection of open dense sets in R, a violation of the Baire category theoremBaire category theoremThe Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
.
- The zero-set of a derivative of an everywhere differentiable real-valued function on R is a Gδ set; it can be a dense set with empty interior, as shown by Pompeiu's construction.
A more elaborate example of a Gδ set is given by the following theorem:
Theorem: The set
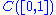is dense in and contains a Gδ subset of the metric space Properties
The notion of Gδ sets in metricMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(and topological
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
) spaces is strongly related to the notion of completeness of the metric space as well as to the Baire category theorem
Baire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
. This is described by the Mazurkiewicz
Mazurkiewicz
Mazurkiewicz is a Polish or Belorussian surname.Notable people with this surname include:* Jan Mazurkiewicz, Polish underground soldier during WW2 and later a general* Ladislao Mazurkiewicz, Uruguayan goalkeeper...
theorem:
Theorem (Mazurkiewicz
Mazurkiewicz
Mazurkiewicz is a Polish or Belorussian surname.Notable people with this surname include:* Jan Mazurkiewicz, Polish underground soldier during WW2 and later a general* Ladislao Mazurkiewicz, Uruguayan goalkeeper...
): Let
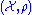be a complete metric space and 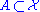. Then the following are equivalent:
-
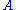is a Gδ subset of 
- There is a metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on 
which is equivalent to 
such that 
is a complete metric space.
A key property of
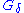sets is that they are the possible sets at which a function from a topological space to a metric space is continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Formally: The set of points where a function
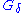is continuous is a set. This is because continuity at a point 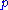can be defined by a 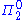formula, namely: For all positive integers , there is an open set containing such that 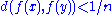for all 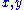in . If a value of is fixed, the set of 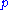for which there is such a corresponding open is itself an open set (being a union of open sets), and the universal quantifier on corresponds to the (countable) intersection of these sets. In the real line, the converse holds as well; for any Gδ subset A of the real line, there is a function f: R → R which is continuous exactly at the points in A. As a consequence, while it is possible for the irrationals to be the set of continuity points of a function (see the popcorn functionPopcorn function
Thomae's function, named after Carl Johannes Thomae, also known as the popcorn function, the raindrop function, the modified Dirichlet function, the ruler function, the Riemann function or the Stars over Babylon is a modification of the Dirichlet function...
), it is impossible to construct a function which is continuous only on the rational numbers.
Basic properties
- The complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of a Gδ set is an Fσ set.
- The intersection of countably many Gδ sets is a Gδ set, and the union of finitely many Gδ sets is a Gδ set; a countable union of Gδ sets is called a Gδσ set.
- In metrizable spaces, every closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
is a Gδ set and, dually, every open set is an Fσ set.
- A subspace A of a topologically complete space X is itself topologically complete if and only if A is a Gδ set in X.
- A set that contains the intersection of a countable collection of denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
open sets is called comeagre or residual. These sets are used to define generic propertiesGeneric propertyIn mathematics, properties that hold for "typical" examples are called generic properties. For instance, a generic property of a class of functions is one that is true of "almost all" of those functions, as in the statements, "A generic polynomial does not have a root at zero," or "A generic...
of topological spaces of functions.
The following results regard Polish space
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
s:
- Let
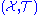be a Polish topological spacePolish spaceIn the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
and let
be a Gδ set (with respect to 
). The 
is a Polish space with respect to the subspace topologySubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
on it.
- Topological characterization of Polish spaces: If
is a Polish spacePolish spaceIn the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
then it is homeomorphicHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to a Gδ subset of a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
.
Gδ space
A Gδ space is a topological space in which every closed setClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
is a Gδ set (Johnson, 1970). A normal space
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
which is also a Gδ space is perfectly normal. Every metrizable space is perfectly normal, and every perfectly normal space is completely normal: neither implication is reversible.
See also
- Fσ set, the dualDuality (mathematics)In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
concept; note that "G" is German (Gebiet) and "F" is French (fermé).