Popcorn function
Encyclopedia
Thomae's function, named after Carl Johannes Thomae
, also known as the popcorn function, the raindrop function, the modified Dirichlet function, the ruler function, the Riemann function
or the Stars over Babylon (by John Horton Conway
) is a modification of the Dirichlet function. This real
-valued function
f(x) is defined as follows:
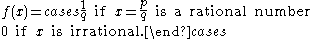
If x = 0 we take q = 1. It is assumed here that gcd
(p, q) = 1 and q > 0 so that the function is well-defined and non-negative.
: f is continuous at all irrational numbers and discontinuous at all rational numbers.
in the reals, for any rational x, no matter what ε we select, there is an irrational a even nearer to our x where f(a) = 0 (while f(x) is positive). In other words, f can never get "close" to any positive number because its image is dense with zeroes.
To show continuity at the irrationals, assume without loss of generality that our ε is rational (for any irrational ε, we can choose a smaller rational ε and the proof is transitive). Since ε is rational, it can be expressed in lowest terms as a/b. We want to show that f(x) is continuous when x is irrational.
Note that f takes a maximum value of 1 at each whole integer, so we may limit our examination to the space between
and 
. Since ε has a finite denominator of b, the only values for which f may return a value greater than ε are those with a reduced denominator no larger than b. There exist only a finite number of values between two integers with denominator no larger than b, so these can be exhaustively listed. Setting δ to be smaller than the nearest distance from x to one of these values guarantees every value within δ of x has f(x) < ε.
. Since the set of all discontinuities is the rational numbers, and the rational numbers are countable, the set has measure zero. As well, the function is bounded on the interval [0,1], so by the Lebesgue criterion, the function is Riemann integrable on [0,1].
.
A variant of the popcorn function can be used to show that any F-sigma subset of the real numbers can be the set of discontinuities of a function. If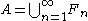
is a countable union of closed sets 
, define
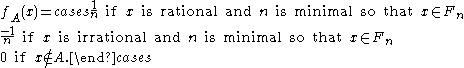
Then a similar argument as for the popcorn function shows that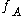
has A as its set of discontinuities.
Carl Johannes Thomae
Carl Johannes Thomae was a German mathematician.-Biography:...
, also known as the popcorn function, the raindrop function, the modified Dirichlet function, the ruler function, the Riemann function
Riemann function
Riemann function may refer to one of the several functions named after the mathematician Bernhard Riemann, including:*Riemann zeta function*Thomae's function*Riemann theta function....
or the Stars over Babylon (by John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
) is a modification of the Dirichlet function. This real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f(x) is defined as follows:
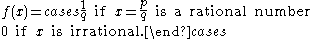
If x = 0 we take q = 1. It is assumed here that gcd
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(p, q) = 1 and q > 0 so that the function is well-defined and non-negative.
Discontinuities
The popcorn function is perhaps the simplest example of a function with a complicated set of discontinuitiesContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
: f is continuous at all irrational numbers and discontinuous at all rational numbers.
Informal Proof
Clearly, f is discontinuous at all rational numbers: since the irrationals are denseDense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in the reals, for any rational x, no matter what ε we select, there is an irrational a even nearer to our x where f(a) = 0 (while f(x) is positive). In other words, f can never get "close" to any positive number because its image is dense with zeroes.
To show continuity at the irrationals, assume without loss of generality that our ε is rational (for any irrational ε, we can choose a smaller rational ε and the proof is transitive). Since ε is rational, it can be expressed in lowest terms as a/b. We want to show that f(x) is continuous when x is irrational.
Note that f takes a maximum value of 1 at each whole integer, so we may limit our examination to the space between
and . Since ε has a finite denominator of b, the only values for which f may return a value greater than ε are those with a reduced denominator no larger than b. There exist only a finite number of values between two integers with denominator no larger than b, so these can be exhaustively listed. Setting δ to be smaller than the nearest distance from x to one of these values guarantees every value within δ of x has f(x) < ε.Integrability
The Lebesgue criterion for integrability states that a bounded function is Riemann integrable if and only if the set of all discontinuities has measure zeroLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. Since the set of all discontinuities is the rational numbers, and the rational numbers are countable, the set has measure zero. As well, the function is bounded on the interval [0,1], so by the Lebesgue criterion, the function is Riemann integrable on [0,1].
Follow-up
A natural followup question one might ask is if there is a function which is continuous on the rational numbers and discontinuous on the irrational numbers. This turns out to be impossible; the set of discontinuities of any function must be an Fσ set. If such a function existed, then the irrationals would be F-sigma and hence would also be a meager set. It would follow that the real numbers, being a union of the irrationals and the rationals (which is evidently meager), would also be a meager set. This would contradict the Baire category theoremBaire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
.
A variant of the popcorn function can be used to show that any F-sigma subset of the real numbers can be the set of discontinuities of a function. If
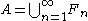is a countable union of closed sets , define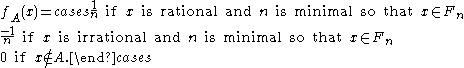Then a similar argument as for the popcorn function shows that
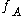has A as its set of discontinuities.See also
- Euclid's orchardEuclid's orchardIn mathematics Euclid's orchard is an array of one-dimensional trees of unit height planted at the lattice points in one quadrant of a square lattice...
– Thomae's function can be interpreted as a perspective drawing of Euclid's orchard