Barometric formula
Encyclopedia
The barometric formula, sometimes called the exponential
atmosphere
or isothermal atmosphere
, is a formula
used to model how the pressure
(or density
) of the air changes with altitude
.
is not equal to zero; the second equation is used when standard temperature lapse rate equals zero.
Equation 1:
Equation 2: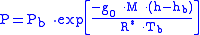
where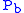
= Static pressure (pascals)
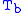= Standard temperature (K
)
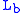= Standard temperature lapse rate -0.0065 (K/m) in ISA
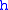= Height above sea level (meters)
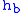= Height at bottom of layer b (meters; e.g., 
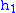= 11,000 meters)
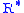= Universal gas constant for air: 8.31432 N·m /(mol·K)
= Gravitational acceleration (9.80665 m/s2)
= Molar mass of Earth's air (0.0289644 kg/mol)
Or converted to English units:
where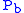
= Static pressure (inches of mercury, inHg)
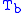= Standard temperature (K)
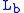= Standard temperature lapse rate (K/ft)
= Height above sea level (ft)
= Height at bottom of layer b (feet; e.g., 
= 36,089 ft)
= Universal gas constant; using feet, kelvins, and (SI) moles
: 8.9494596×104 lb·ft2/(lbmol·K·s2)
= Gravitational acceleration (32.17405 ft/s2)
= Molar mass of Earth's air (28.9644 lb/lbmol)
The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. In these equations, g0, M and R* are each single-valued constants, while P, L, T, and h are multivalued constants in accordance with the table below. The values used for M, g0, and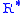
are in accordance with the U.S. Standard Atmosphere, 1976, and the value for 
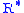in particular does not agree with standard values for this constant. The reference value for Pb for b = 0 is the defined sea level value, P0 = 101325 pascals
or 29.92126 inHg. Values of Pb of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when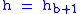
.:
There are two different equations for computing density at various height regimes below 86 geometric km (84,852 geopotential meters or 278,385.8 geopotential feet). The first equation is used when the value of Standard Temperature Lapse rate is not equal to zero; the second equation is used when Standard Temperature Lapse rate equals zero.
Equation 1:
Equation 2:
where
= Mass density (kg/m3)
= Standard temperature (K)
= Standard temperature lapse rate (see table below) (K/m) in ISA
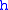= Height above sea level (geopotential meters)
= Universal gas constant for air: 8.31432 N·m/(mol·K)
= Gravitational acceleration (9.80665 m/s2)
= Molar mass of Earth's air (0.0289644 kg/mol)
Or converted to English gravitational foot-pound-second units:
Where
= Mass density (slug/ft3)
= Standard temperature (kelvins)
= Standard temperature lapse rate (degrees Celsius per foot)
= Height above sea level (geopotential feet)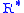
= Universal gas constant (8.9494596×104 ft2/(s·°C)
= Gravitational acceleration (32.17405 ft/s2)
= Molar mass of Earth's air (0.0289644 kg/mol)
The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. The reference value for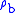
for b = 0 is the defined sea level value, 
= 1.2250 kg/m3 or 0.0023768908 slug/ft3. Values of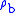 
of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when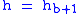 
In these equations, g0, M and R* are each single-valued constants, while
, L, T and h are multi-valued constants in accordance with the table below. The values used for M, g0 and R* are in accordance with the U.S. Standard Atmosphere, 1976, and that the value for R* in particular does not agree with standard values for this constant.
:
When density is known:
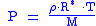
And assuming that all pressure is hydrostatic:
Dividing the
by the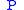 
expression we get:
Integrating
this expression from the surface to the altitude z we get:
Assuming constant temperature, molar mass, and gravitational acceleration, we get the barometric formula:
In this formulation,
is the gas constant
, and the term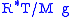
gives the scale height
(approximately equal to 8.4 km for the troposphere
).
(For exact results, it should be remembered that atmospheres containing water do not behave as an ideal gas. See real gas
or perfect gas
or gas
to further understanding)
is constant throughout the planet, we can get a rough estimate of a constant temperature.
The solar energy flux at a distance
can be estimated as:
where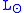
is the solar luminosity. The actual incoming energy can be estimated as
where
is the albedo
of the planet.
is the radius of the planet and 
is the distance to the Sun
in astronomical unit
s.
The outgoing energy can be estimated using the Stefan-Boltzmann's law
where
is the Stefan–Boltzmann constant and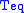 
is the temperature
at equilibrium.
Solving the equation:
leads to the following estimate of a planet's temperature
which for Earth is about 255 K or −18 °C
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
atmosphere
Earth's atmosphere
The atmosphere of Earth is a layer of gases surrounding the planet Earth that is retained by Earth's gravity. The atmosphere protects life on Earth by absorbing ultraviolet solar radiation, warming the surface through heat retention , and reducing temperature extremes between day and night...
or isothermal atmosphere
Atmosphere
An atmosphere is a layer of gases that may surround a material body of sufficient mass, and that is held in place by the gravity of the body. An atmosphere may be retained for a longer duration, if the gravity is high and the atmosphere's temperature is low...
, is a formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
used to model how the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
(or density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
) of the air changes with altitude
Altitude
Altitude or height is defined based on the context in which it is used . As a general definition, altitude is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The reference datum also often varies according to the context...
.
Pressure equations
There are two different equations for computing pressure at various height regimes below 86 km (or 278,400 feet). The first equation is used when the value of Standard Temperature Lapse RateLapse rate
The lapse rate is defined as the rate of decrease with height for an atmospheric variable. The variable involved is temperature unless specified otherwise. The terminology arises from the word lapse in the sense of a decrease or decline; thus, the lapse rate is the rate of decrease with height and...
is not equal to zero; the second equation is used when standard temperature lapse rate equals zero.
Equation 1:
Equation 2:
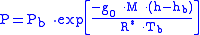
where
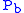= Static pressure (pascals) 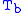= Standard temperature (KKelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
)
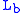= Standard temperature lapse rate -0.0065 (K/m) in ISAInternational Standard Atmosphere
The International Standard Atmosphere is an atmospheric model of how the pressure, temperature, density, and viscosity of the Earth's atmosphere change over a wide range of altitudes. It has been established to provide a common reference for temperature and pressure and consists of tables of...
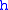= Height above sea level (meters) 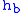= Height at bottom of layer b (meters; e.g., 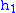= 11,000 meters) 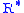= Universal gas constant for air: 8.31432 N·m /(mol·K) = Gravitational acceleration (9.80665 m/s2) = Molar mass of Earth's air (0.0289644 kg/mol)Or converted to English units:
where
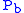= Static pressure (inches of mercury, inHg) 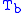= Standard temperature (K) 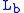= Standard temperature lapse rate (K/ft) = Height above sea level (ft) = Height at bottom of layer b (feet; e.g., = 36,089 ft) = Universal gas constant; using feet, kelvins, and (SI) molesMole (unit)
The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
: 8.9494596×104 lb·ft2/(lbmol·K·s2)
= Gravitational acceleration (32.17405 ft/s2) = Molar mass of Earth's air (28.9644 lb/lbmol)The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. In these equations, g0, M and R* are each single-valued constants, while P, L, T, and h are multivalued constants in accordance with the table below. The values used for M, g0, and
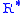are in accordance with the U.S. Standard Atmosphere, 1976, and the value for 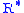in particular does not agree with standard values for this constant. The reference value for Pb for b = 0 is the defined sea level value, P0 = 101325 pascalsPascal (unit)
The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...
or 29.92126 inHg. Values of Pb of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when
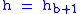.:| Subscript b | Height above sea level | Static pressure | Standard temperature (K) |
Temperature lapse rate | |||
|---|---|---|---|---|---|---|---|
| (m) | (ft) | (pascals) | (inHg) | (K/m) | (K/ft) | ||
| 0 | 0 | 0 | 101325 | 29.92126 | 288.15 | -0.0065 | -0.0019812 |
| 1 | 11,000 | 36,089 | 22632.1 | 6.683245 | 216.65 | 0.0 | 0.0 |
| 2 | 20,000 | 65,617 | 5474.89 | 1.616734 | 216.65 | 0.001 | 0.0003048 |
| 3 | 32,000 | 104,987 | 868.019 | 0.2563258 | 228.65 | 0.0028 | 0.00085344 |
| 4 | 47,000 | 154,199 | 110.906 | 0.0327506 | 270.65 | 0.0 | 0.0 |
| 5 | 51,000 | 167,323 | 66.9389 | 0.01976704 | 270.65 | -0.0028 | -0.00085344 |
| 6 | 71,000 | 232,940 | 3.95642 | 0.00116833 | 214.65 | -0.002 | -0.0006096 |
Density equations
The expressions for calculating density are nearly identical to calculating pressure. The only difference is the exponent in Equation 1.There are two different equations for computing density at various height regimes below 86 geometric km (84,852 geopotential meters or 278,385.8 geopotential feet). The first equation is used when the value of Standard Temperature Lapse rate is not equal to zero; the second equation is used when Standard Temperature Lapse rate equals zero.
Equation 1:
Equation 2:
where
= Mass density (kg/m3) = Standard temperature (K) = Standard temperature lapse rate (see table below) (K/m) in ISAInternational Standard Atmosphere
The International Standard Atmosphere is an atmospheric model of how the pressure, temperature, density, and viscosity of the Earth's atmosphere change over a wide range of altitudes. It has been established to provide a common reference for temperature and pressure and consists of tables of...
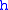= Height above sea level (geopotential meters) = Universal gas constant for air: 8.31432 N·m/(mol·K) = Gravitational acceleration (9.80665 m/s2) = Molar mass of Earth's air (0.0289644 kg/mol)Or converted to English gravitational foot-pound-second units:
Where
= Mass density (slug/ft3) = Standard temperature (kelvins) = Standard temperature lapse rate (degrees Celsius per foot) = Height above sea level (geopotential feet)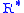 = Universal gas constant (8.9494596×104 ft2/(s·°C) = Gravitational acceleration (32.17405 ft/s2) = Molar mass of Earth's air (0.0289644 kg/mol)The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. The reference value for
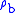for b = 0 is the defined sea level value, = 1.2250 kg/m3 or 0.0023768908 slug/ft3. Values of 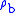of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when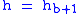 In these equations, g0, M and R* are each single-valued constants, while
, L, T and h are multi-valued constants in accordance with the table below. The values used for M, g0 and R* are in accordance with the U.S. Standard Atmosphere, 1976, and that the value for R* in particular does not agree with standard values for this constant.| Subscript b | Height Above Sea Level (h) | Mass Density ( ) |
Standard Temperature (T) (K) |
Temperature Lapse Rate (L) | |||
|---|---|---|---|---|---|---|---|
| (m) | (ft) | (kg/m3) | (slugs/ft3) | (K/m) | (K/ft) | ||
| 0 | 0 | 0 | 1.2250 | 2.3768908 x 10−3 | 288.15 | -0.0065 | -0.0019812 |
| 1 | 11,000 | 36,089.24 | 0.36391 | 7.0611703 x 10−4 | 216.65 | 0.0 | 0.0 |
| 2 | 20,000 | 65,616.79 | 0.08803 | 1.7081572 x 10−4 | 216.65 | 0.001 | 0.0003048 |
| 3 | 32,000 | 104,986.87 | 0.01322 | 2.5660735 x 10−5 | 228.65 | 0.0028 | 0.00085344 |
| 4 | 47,000 | 154,199.48 | 0.00143 | 2.7698702 x 10 |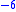
270.65 | 0.0 | 0.0 |
| 5 | 51,000 | 167,322.83 | 0.00086 | 1.6717895 x 10−6 | 270.65 | -0.0028 | -0.00085344 |
| 6 | 71,000 | 232,939.63 | 0.000064 | 1.2458989 x 10−7 | 214.65 | -0.002 | -0.0006096 |
Derivation
The barometric formula can be derived fairly easily using the ideal gas lawIdeal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
:
When density is known:
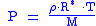
And assuming that all pressure is hydrostatic:
Dividing the
by the 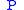expression we get:Integrating
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
this expression from the surface to the altitude z we get:
Assuming constant temperature, molar mass, and gravitational acceleration, we get the barometric formula:
In this formulation,
is the gas constantGas constant
The gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
, and the term
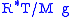gives the scale heightScale height
In various scientific contexts, a scale height is a distance over which a quantity decreases by a factor of e...
(approximately equal to 8.4 km for the troposphere
Troposphere
The troposphere is the lowest portion of Earth's atmosphere. It contains approximately 80% of the atmosphere's mass and 99% of its water vapor and aerosols....
).
(For exact results, it should be remembered that atmospheres containing water do not behave as an ideal gas. See real gas
Real gas
Real gases – as opposed to a perfect or ideal gas – exhibit properties that cannot be explained entirely using the ideal gas law. To understand the behaviour of real gases, the following must be taken into account:* compressibility effects;...
or perfect gas
Perfect gas
In physics, a perfect gas is a theoretical gas that differs from real gases in a way that makes certain calculations easier to handle. Its behavior is more simplified compared to an ideal gas...
or gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
to further understanding)
Estimating the temperature
Assuming that the only energy source is from the sun, and the albedoAlbedo
Albedo , or reflection coefficient, is the diffuse reflectivity or reflecting power of a surface. It is defined as the ratio of reflected radiation from the surface to incident radiation upon it...
is constant throughout the planet, we can get a rough estimate of a constant temperature.
The solar energy flux at a distance
can be estimated as:where
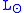is the solar luminosity. The actual incoming energy can be estimated aswhere
is the albedoAlbedo
Albedo , or reflection coefficient, is the diffuse reflectivity or reflecting power of a surface. It is defined as the ratio of reflected radiation from the surface to incident radiation upon it...
of the planet.
is the radius of the planet and is the distance to the SunSun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
in astronomical unit
Astronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
s.
The outgoing energy can be estimated using the Stefan-Boltzmann's law
where
is the Stefan–Boltzmann constant and 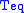is the temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
at equilibrium.
Solving the equation:
leads to the following estimate of a planet's temperature
which for Earth is about 255 K or −18 °C