
Fermat's Last Theorem
Encyclopedia

Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Fermat's Last Theorem states that no three positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two.
This theorem was first conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
d by Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
in 1637, famously in the margin of a copy of Arithmetica
Arithmetica
Arithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
where he claimed he had a proof that was too large to fit in the margin. No successful proof was published until 1995 despite the efforts of countless mathematicians during the 358 intervening years. The unsolved problem stimulated the development of algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
in the 19th century and the proof of the modularity theorem in the 20th. It is among the most famous theorems in the history of mathematics
History of mathematics
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
and prior to its 1995 proof
Wiles' proof of Fermat's Last Theorem
Wiles's proof of Fermat's Last Theorem is a proof of the modularity theorem for semistable elliptic curves released by Andrew Wiles, which, together with Ribet's theorem, provides a proof for Fermat's Last Theorem. Wiles first announced his proof in June 1993 in a version that was soon recognized...
was in the Guinness Book of World Records for "most difficult math problems".
Fermat's conjecture (History)
Fermat left no proof of the conjecture for all n, but he did prove the special case n = 4. This reduced the problem to proving the theorem for exponents n that are prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. Over the next two centuries (1637–1839), the conjecture was proven for only the primes 3, 5, and 7, although Sophie Germain
Sophie Germain
Marie-Sophie Germain was a French mathematician, physicist, and philosopher. Despite initial opposition from her parents and difficulties presented by a gender-biased society, she gained education from books in her father's library and from correspondence with famous mathematicians such as...
proved a special case for all primes less than 100. In the mid-19th century, Ernst Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
proved the theorem for regular primes. Building on Kummer's work and using sophisticated computer studies, other mathematicians were able to prove the conjecture for all odd primes up to four million.
The final proof of the conjecture for all n came in the late 20th century. In 1984, Gerhard Frey
Gerhard Frey
Gerhard Frey is a German mathematician, known for his work in number theory. His Frey curve, a construction of an elliptic curve from a purported solution to the Fermat equation, was central to Wiles' proof of Fermat's Last Theorem....
suggested the approach of proving the conjecture through a proof of the modularity theorem for elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s. Building on work of Ken Ribet, Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
succeeded in proving enough of the modularity theorem to prove Fermat's Last Theorem, with the assistance of Richard Taylor
Richard Taylor (mathematician)
-External links:**...
. Wiles's achievement was reported widely in the popular press, and has been popularized in books and television programs.
Pythagorean triples
Pythagorean triples are a set of three integers (a, b, c) that satisfy a special case of Fermat's equation (n = 2)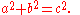
Examples of Pythagorean triples include (3, 4, 5) and (5, 12, 13). There are infinitely many such triples, and methods for generating such triples have been studied in many cultures, beginning with the Babylonians
Babylonian mathematics
Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
and later ancient Greek
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
, Chinese
Chinese mathematics
Mathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry....
and Indian
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
mathematicians. The traditional interest in Pythagorean triples connects with the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
; in its converse form, it states that a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
with sides of lengths a, b and c has a right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
between the a and b legs when the numbers are a Pythagorean triple. Right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
s have various practical applications, such as surveying
Surveying
See Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...
, carpentry
Carpentry
A carpenter is a skilled craftsperson who works with timber to construct, install and maintain buildings, furniture, and other objects. The work, known as carpentry, may involve manual labor and work outdoors....
, masonry
Masonry
Masonry is the building of structures from individual units laid in and bound together by mortar; the term masonry can also refer to the units themselves. The common materials of masonry construction are brick, stone, marble, granite, travertine, limestone; concrete block, glass block, stucco, and...
and construction
Construction
In the fields of architecture and civil engineering, construction is a process that consists of the building or assembling of infrastructure. Far from being a single activity, large scale construction is a feat of human multitasking...
. Fermat's Last Theorem is an extension of this problem to higher powers, stating that no solution exists when the exponent 2 is replaced by any larger integer.
Diophantine equations
Fermat's equation xn + yn = zn is an example of a Diophantine equation. A Diophantine equation is a polynomial equation in which the solutions must be integers. Their name derives from the 3rd-century AlexandriaAlexandria
Alexandria is the second-largest city of Egypt, with a population of 4.1 million, extending about along the coast of the Mediterranean Sea in the north central part of the country; it is also the largest city lying directly on the Mediterranean coast. It is Egypt's largest seaport, serving...
n mathematician, Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
, who developed methods for their solution. A typical Diophantine problem is to find two integers x and y such that their sum, and the sum of their squares, equal two given numbers A and B, respectively:
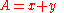

Diophantus's major work is the Arithmetica
Arithmetica
Arithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
, of which only a portion has survived. Fermat's conjecture of his Last Theorem was inspired while reading a new edition of the Arithmetica, which was translated into Latin and published in 1621 by Claude Bachet
Claude Gaspard Bachet de Méziriac
Claude Gaspard Bachet de Méziriac was a French mathematician, linguist, poet and classics scholar born in Bourg-en-Bresse.Bachet was a pupil of the Jesuit mathematician Jacques de Billy at the Jesuit College in Rheims...
.
Diophantine equations have been studied for thousands of years. For example, the solutions to the quadratic Diophantine equation x2 + y2 = z2 are given by the Pythagorean triple
Pythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
s, originally solved by the Babylonians (c. 1800 BC). Solutions to linear Diophantine equations, such as 26x + 65y = 13, may be found using the Euclidean algorithm
Euclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
(c. 5th century BC).
Many Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s have a form similar to the equation of Fermat's Last Theorem from the point of view of algebra, in that they have no cross terms mixing two letters, without sharing its particular properties. For example, it is known that there are infinitely many positive integers x, y, and z such that xn + yn = zm where n and m are relatively prime natural numbers.For example,
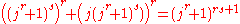
Fermat's conjecture

Arithmetica
Arithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
asks how a given square number is split into two other squares; in other words, for a given rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
k, find rational numbers u and v such that k2 = u2 + v2. Diophantus shows how to solve this sum-of-squares problem for k = 4 (the solutions being u = 16/5 and v = 12/5).
Around 1637, Fermat wrote his Last Theorem in the margin of his copy of the Arithmetica next to Diophantus' sum-of-squares problem:
| Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet. | it is impossible to separate a cube into two cubes, or a fourth power into two fourth powers, or in general, any power higher than the second, into two like powers. I have discovered a truly marvelous proof of this, which this margin is too narrow to contain. |
Although Fermat's general proof is unknown, his proof of one case (n = 4) by infinite descent
Infinite descent
In mathematics, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that...
has survived. Fermat posed the cases of n = 4 and of n = 3 as challenges to his mathematical correspondents, such as Marin Mersenne
Marin Mersenne
Marin Mersenne, Marin Mersennus or le Père Mersenne was a French theologian, philosopher, mathematician and music theorist, often referred to as the "father of acoustics"...
, Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
, and John Wallis. However, in the last thirty years of his life, Fermat never again wrote of his "truly marvellous proof" of the general case.
After Fermat's death in 1665, his son Clément-Samuel Fermat produced a new edition of the book (1670) augmented with his father's comments. The margin note became known as Fermat's Last Theorem, as it was the last of Fermat's asserted theorems to remain unproven.
Proofs for specific exponents
Only one mathematical proof by Fermat has survived, in which Fermat uses the technique of infinite descent to show that the area of a right triangle with integer sides can never equal the square of an integer. His proof is equivalent to demonstrating that the equation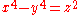
has no primitive solutions in integers (no pairwise coprime
Pairwise coprime
In mathematics, especially number theory, a set of integers is said to be pairwise coprime if every pair of distinct integers a and b in the set are coprime...
solutions). In turn, this proves Fermat's Last Theorem for the case n=4, since the equation a4 + b4 = c4 can be written as c4 − b4 = (a2)2. For a version of Fermat's proof by infinite descent, see Infinite descent#Non-solvability of r2 + s4 = t4. For various proofs by infinite descent, see Grant and Perella (1999), Barbara (2007), and Dolan (2011).
Alternative proofs of the case n = 4 were developed later by Frénicle de Bessy
Bernard Frénicle de Bessy
Bernard Frénicle de Bessy , was a French mathematician born in Paris, who wrote numerous mathematical papers, mainly in number theory and combinatorics. He is best remembered for Des quarrez ou tables magiques, a treatise on magic squares published posthumously in 1693, in which he described all...
(1676), Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
(1738), Kausler (1802), Peter Barlow (1811), Adrien-Marie Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
(1830), Schopis (1825), Terquem (1846), Joseph Bertrand
Joseph Louis François Bertrand
Joseph Louis François Bertrand was a French mathematician who worked in the fields of number theory, differential geometry, probability theory, economics and thermodynamics....
(1851), Victor Lebesgue (1853, 1859, 1862), Theophile Pepin (1883), Tafelmacher (1893), David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
(1897), Bendz (1901), Gambioli (1901), Leopold Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
(1901), Bang (1905), Sommer (1907), Bottari (1908), Karel Rychlík
Karel Rychlík
Karel Rychlík was a Czech mathematician who contributed significantly to the fields of algebra, number theory, mathematical analysis, and the history of mathematics.-External links:**...
(1910), Nutzhorn (1912), Robert Carmichael
Robert Daniel Carmichael
Robert Daniel Carmichael was a leading American mathematician. Carmichael was born in Goodwater, Alabama. He attended Lineville College, briefly, and he earned his bachelor's degree in 1898, while he was studying towards his Ph.D. degree at Princeton University. Carmichael completed the...
(1913), Hancock (1931), and Vrǎnceanu (1966).
After Fermat proved the special case n = 4, the general proof for all n required only that the theorem be established for all odd prime exponents. In other words, it was necessary to prove only that the equation an + bn = cn has no integer solutions (a, b, c) when n is an odd prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. This follows because a solution (a, b, c) for a given n is equivalent to a solution for all the factors of n. For illustration, let n be factored into d and e, n = de. The general equation
- an + bn = cn
implies that (ad, bd, cd) is a solution for the exponent e
- (ad)e + (bd)e = (cd)e
Thus, to prove that Fermat's equation has no solutions for n > 2, it suffices to prove that it has no solutions for at least one prime factor of every n. All integers n > 2 contain a factor of 4, or an odd prime number, or both. Therefore, Fermat's Last Theorem can be proven for all n if it can be proven for n = 4 and for all odd primes (the only even prime number is the number 2) p.
In the two centuries following its conjecture (1637–1839), Fermat's Last Theorem was proven for three odd prime exponents p = 3, 5 and 7. The case p = 3 was first stated by Abu-Mahmud Khojandi (10th century), but his attempted proof of the theorem was incorrect. In 1770, Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
gave a proof of p = 3, but his proof by infinite descent contained a major gap. However, since Euler himself had proven the lemma necessary to complete the proof in other work, he is generally credited with the first proof. Independent proofs were published by Kausler (1802), Legendre (1823, 1830), Calzolari (1855), Gabriel Lamé
Gabriel Lamé
Gabriel Léon Jean Baptiste Lamé was a French mathematician.-Biography:Lamé was born in Tours, in today's département of Indre-et-Loire....
(1865), Peter Guthrie Tait
Peter Guthrie Tait
Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
(1872), Günther (1878), Gambioli (1901), Krey (1909), Rychlík (1910), Stockhaus (1910), Carmichael (1915), Johannes van der Corput
Johannes van der Corput
Johannes Gualtherus van der Corput was a Dutch mathematician, working in the field of analytic number theory....
(1915), Axel Thue
Axel Thue
Axel Thue was a Norwegian mathematician, known for highly original work in diophantine approximation, and combinatorics....
(1917), and Duarte (1944). The case p = 5 was proven independently by Legendre and Peter Dirichlet
Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
around 1825. Alternative proofs were developed by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
(1875, posthumous), Lebesgue (1843), Lamé (1847), Gambioli (1901), Werebrusow (1905), Rychlík (1910), van der Corput (1915), and Guy Terjanian
Guy Terjanian
Guy Terjanian is a French-Armenian mathematician who has worked on algebraic number theory. He achieved his Ph.D under Claude Chevalley in 1966, and at that time published a counterexample to the original form of a conjecture of Emil Artin, which suitably modified had just been proved as the...
(1987). The case p = 7 was proven by Lamé in 1839. His rather complicated proof was simplified in 1840 by Lebesgue, and still simpler proofs were published by Angelo Genocchi
Angelo Genocchi
Angelo Genocchi was an Italian mathematician who specialized in number theory. He worked with Giuseppe Peano. The Genocchi numbers are named after him.-References:...
in 1864, 1874 and 1876. Alternative proofs were developed by Théophile Pépin (1876) and Edmond Maillet (1897).
Fermat's Last Theorem has also been proven for the exponents n = 6, 10, and 14. Proofs for n = 6 have been published by Kausler, Thue, Tafelmacher, Lind, Kapferer, Swift, and Breusch. Similarly, Dirichlet and Terjanian each proved the case n = 14, while Kapferer and Breusch each proved the case n = 10. Strictly speaking, these proofs are unnecessary, since these cases follow from the proofs for n = 3, 5, and 7, respectively. Nevertheless, the reasoning of these even-exponent proofs differs from their odd-exponent counterparts. Dirichlet's proof for n = 14 was published in 1832, before Lamé's 1839 proof for n = 7.
Many proofs for specific exponents use Fermat's technique of infinite descent
Infinite descent
In mathematics, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that...
, which Fermat used to prove the case n = 4, but many do not. However, the details and auxiliary arguments are often ad hoc and tied to the individual exponent under consideration. Since they became ever more complicated as p increased, it seemed unlikely that the general case of Fermat's Last Theorem could be proven by building upon the proofs for individual exponents. Although some general results on Fermat's Last Theorem were published in the early 19th century by Niels Henrik Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
and Peter Barlow, the first significant work on the general theorem was done by Sophie Germain
Sophie Germain
Marie-Sophie Germain was a French mathematician, physicist, and philosopher. Despite initial opposition from her parents and difficulties presented by a gender-biased society, she gained education from books in her father's library and from correspondence with famous mathematicians such as...
.
Sophie Germain
In the early 19th century, Sophie GermainSophie Germain
Marie-Sophie Germain was a French mathematician, physicist, and philosopher. Despite initial opposition from her parents and difficulties presented by a gender-biased society, she gained education from books in her father's library and from correspondence with famous mathematicians such as...
developed several novel approaches to prove Fermat's last theorem for all exponents. First, she defined a set of auxiliary primes θ constructed from the prime exponent p by the equation θ = 2hp+1, where h is any integer not divisible by three. She showed that if no integers raised to the pth power were adjacent modulo θ (the non-consecutivity condition), then θ must divide the product xyz. Her goal was to use mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
to prove that, for any given p, infinitely many auxiliary primes θ satisfied the non-consecutivity condition and thus divided xyz; since the product xyz can have at most a finite number of prime factors, such a proof would have established Fermat's Last Theorem. Although she developed many techniques for establishing the non-consecutivity condition, she did not succeed in her strategic goal. She also worked to set lower limits on the size of solutions to Fermat's equation for a given exponent p, a modified version of which was published by Adrien-Marie Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
. As a byproduct of this latter work, she proved Sophie Germain's theorem
Sophie Germain's theorem
In number theory, Sophie Germain's theorem is a statement about the divisibility of solutions to the equation xp + yp = zp of Fermat's Last Theorem...
, which verified the first case of Fermat's Last Theorem for every odd prime exponent less than 100. Germain tried unsuccessfully to prove the first case of Fermat's Last Theorem for all even exponents, specifically for n = 2p, which was proven by Guy Terjanian
Guy Terjanian
Guy Terjanian is a French-Armenian mathematician who has worked on algebraic number theory. He achieved his Ph.D under Claude Chevalley in 1966, and at that time published a counterexample to the original form of a conjecture of Emil Artin, which suitably modified had just been proved as the...
in 1977. In 1985, Leonard Adleman
Leonard Adleman
Leonard Max Adleman is an American theoretical computer scientist and professor of computer science and molecular biology at the University of Southern California. He is known for being a co-inventor of the RSA cryptosystem in 1977, and of DNA computing...
, Roger Heath-Brown
Roger Heath-Brown
David Rodney "Roger" Heath-Brown F.R.S. , is a British mathematician working in the field of analytic number theory. He was an undergraduate and graduate student of Trinity College, Cambridge; his research supervisor was Alan Baker...
and Étienne Fouvry proved that the first case of Fermat's Last Theorem holds for infinitely many odd primes p.
Ernst Kummer and the theory of ideals
In 1847, Gabriel LaméGabriel Lamé
Gabriel Léon Jean Baptiste Lamé was a French mathematician.-Biography:Lamé was born in Tours, in today's département of Indre-et-Loire....
outlined a proof of Fermat's Last Theorem based on factoring the equation xp + yp = zp in complex numbers, specifically the cyclotomic field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
based on the roots of the number 1
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
. His proof failed, however, because it assumed incorrectly that such complex numbers can be factored uniquely into primes, similar to integers. This gap was pointed out immediately by Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
, who later read a paper that demonstrated this failure of unique factorisation, written by Ernst Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
.
Kummer set himself the task of determining whether the cyclotomic field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
could be generalized to include new prime numbers such that unique factorisation was restored. He succeeded in that task by developing the ideal number
Ideal number
In number theory an ideal number is an algebraic integer which represents an ideal in the ring of integers of a number field; the idea was developed by Ernst Kummer, and led to Richard Dedekind's definition of ideals for rings...
s. Using the general approach outlined by Lamé, Kummer proved both cases of Fermat's Last Theorem for all regular prime numbers. However, he could not prove the theorem for the exceptional primes (irregular primes) which conjecturally occur approximately 39% of the time; the only irregular primes below 100 are 37, 59 and 67.
Mordell conjecture
In the 1920s, Louis MordellLouis Mordell
Louis Joel Mordell was a British mathematician, known for pioneering research in number theory. He was born in Philadelphia, USA, in a Jewish family of Lithuanian extraction...
posed a conjecture that implied that Fermat's equation has at most a finite number of nontrivial primitive integer solutions if the exponent n is greater than two. This conjecture was proven in 1983 by Gerd Faltings
Gerd Faltings
Gerd Faltings is a German mathematician known for his work in arithmetic algebraic geometry.From 1972 to 1978, he studied mathematics and physics at the University of Münster. In 1978 he received his PhD in mathematics and in 1981 he got the venia legendi in mathematics, both from the University...
, and is now known as Faltings' theorem
Faltings' theorem
In number theory, the Mordell conjecture is the conjecture made by that a curve of genus greater than 1 over the field Q of rational numbers has only finitely many rational points. The conjecture was later generalized by replacing Q by a finite extension...
.
Computational studies
In the latter half of the 20th century, computational methods were used to extend Kummer's approach to the irregular primes. In 1954, Harry VandiverHarry Vandiver
Harry Schultz Vandiver was an American mathematician, known for work in number theory.He was born in Philadelphia, Pennsylvania to John Lyon and Ida Frances Vandiver...
used a SWAC computer
SWAC (computer)
The SWAC was an early electronic digital computer built in 1950 by the U.S. National Bureau of Standards in Los Angeles, California. It was designed by Harry Huskey...
to prove Fermat's Last Theorem for all primes up to 2521. By 1978, Samuel Wagstaff had extended this to all primes less than 125,000. By 1993, Fermat's Last Theorem had been proven for all primes less than four million.
Connection with elliptic curves
The ultimately successful strategy for proving Fermat's Last Theorem was by proving the modularity theorem. The strategy was first described by Gerhard FreyGerhard Frey
Gerhard Frey is a German mathematician, known for his work in number theory. His Frey curve, a construction of an elliptic curve from a purported solution to the Fermat equation, was central to Wiles' proof of Fermat's Last Theorem....
in 1984. Frey noted that if Fermat's equation had a solution (a, b, c) for exponent p > 2, the corresponding elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
This elliptic curve was first suggested in the 1960s by Yves Hellegouarch, but he did not call attention to its non-modularity. For more details, see
- y2 = x (x − ap)(x + bp)
would have such unusual properties that the curve would likely violate the modularity theorem. This theorem, first conjectured in the mid-1950s and gradually refined through the 1960s, states that every elliptic curve is modular
Modular elliptic curve
A modular elliptic curve is an elliptic curve E that admits a parametrisation X0 → E by a modular curve. This is not the same as a modular curve that happens to be an elliptic curve, and which could be called an elliptic modular curve...
, meaning that it can be associated with a unique modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
.
Following this strategy, the proof of Fermat's Last Theorem required two steps. First, it was necessary to show that Frey's intuition was correct, that the above elliptic curve is always non-modular. Frey did not succeed in proving this rigorously; the missing piece was identified by Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
. This missing piece, the so-called "epsilon conjecture", was proven by Ken Ribet in 1986. Second, it was necessary to prove a special case of the modularity theorem. This special case (for semistable elliptic curve
Semistable elliptic curve
In algebraic geometry, a semistable abelian variety is an abelian variety defined over a global or local field, which is characterized by how it reduces at the primes of the field....
s) was proven by Andrew Wiles in 1995.
Thus, the epsilon conjecture showed that any solution to Fermat's equation could be used to generate a non-modular semistable elliptic curve, whereas Wiles' proof showed that all such elliptic curves must be modular. This contradiction implies that there can be no solutions to Fermat's equation, thus proving Fermat's Last Theorem.
Wiles' general proof

Iwasawa theory
In number theory, Iwasawa theory is the study of objects of arithmetic interest over infinite towers of number fields. It began as a Galois module theory of ideal class groups, initiated by Kenkichi Iwasawa, in the 1950s, as part of the theory of cyclotomic fields. In the early 1970s, Barry Mazur...
, but by the summer of 1991, this approach seemed inadequate to the task. In response, he exploited an Euler system
Euler system
In mathematics, an Euler system is collection of compatible elements of Galois cohomology groups indexed by fields. They were introduced by in his work on Heegner points on modular elliptic curves, which was motivated by his earlier paper and the work of...
recently developed by Victor Kolyvagin
Victor Kolyvagin
Victor Alexandrovich Kolyvagin is a Russian mathematician who wrote a series of papers on Euler systems, leading to breakthroughs on the Birch and Swinnerton-Dyer conjecture, and Iwasawa's conjecture for cyclotomic fields. His work also influenced Andrew Wiles's work on Fermat's Theorem.Kolyvagin...
and Matthias Flach. Since Wiles was unfamiliar with such methods, he asked his Princeton colleague, Nick Katz
Nick Katz
Nicholas Michael Katz is an American mathematician, working in the fields of algebraic geometry, particularly on p-adic methods, monodromy and moduli problems, and number theory...
, to check his reasoning over the spring semester of 1993.
By mid-1993, Wiles was sufficiently confident of his results that he presented them in three lectures delivered on June 21–23, 1993 at the Isaac Newton Institute for Mathematical Sciences. Specifically, Wiles presented his proof of the Taniyama–Shimura conjecture for semistable elliptic curves; together with Ribet's proof of the epsilon conjecture, this implied Fermat's Last Theorem. However, it soon became apparent that Wiles' initial proof was incorrect. A critical portion of the proof contained an error in a bound on the order of a particular group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. The error was caught by several mathematicians refereeing Wiles' manuscript, including Katz, who alerted Wiles on 23 August 1993.
Wiles and his former student Richard Taylor
Richard Taylor (mathematician)
-External links:**...
spent almost a year trying to repair the proof, without success. On 19 September 1994, Wiles had a flash of insight that the proof could be saved by returning to his original Horizontal Iwasawa theory approach, which he had abandoned in favour of the Kolyvagin–Flach approach. On 24 October 1994, Wiles submitted two manuscripts, "Modular elliptic curves and Fermat's Last Theorem" and "Ring theoretic properties of certain Hecke algebras", the second of which was co-authored with Taylor. The two papers were vetted and published as the entirety of the May 1995 issue of the Annals of Mathematics
Annals of Mathematics
The Annals of Mathematics is a bimonthly mathematical journal published by Princeton University and the Institute for Advanced Study. It ranks amongst the most prestigious mathematics journals in the world by criteria such as impact factor.-History:The journal began as The Analyst in 1874 and was...
. These papers established the modularity theorem for semistable elliptic curves, the last step in proving Fermat's Last Theorem, 358 years after it was conjectured.
Rational exponents
All solutions of the Diophantine equation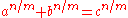 when n=1 were computed by Lenstra in 1992. In the case in which the mth roots are required to be real and positive, all solutions are given by
when n=1 were computed by Lenstra in 1992. In the case in which the mth roots are required to be real and positive, all solutions are given by
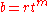

for positive integers r, s, t with s and t coprime.
In 2004, for n>2, Bennett, Glass, and Szekely proved that if gcd(n,m)=1, then there are integer solutions if and only if 6 divides m, and
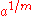 ,
, 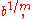 and
and 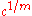 are different complex 6th roots of the same real number.
are different complex 6th roots of the same real number.n = –1
All primitive (pairwise coprime) integer solutions to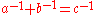 can be written as
can be written as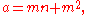
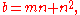

for positive, coprime integers m, n.
n = –2
The case n = –2 also has an infinitude of solutions, and these have a geometric interpretation in terms of right triangles with integer sides and an integer altitude to the hypotenuse. All primitive solutions to are given by
are given by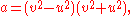
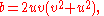
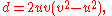
for coprime integers u, v with v > u. The geometric interpretation is that a and b are the integer legs of a right triangle and d is the integer altitude to the hypotenuse. Then the hypotenuse itself is the integer

so (a, b, c) is a Pythagorean triple
Pythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
.
Integer n < –2
There are no solutions in integers for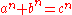 for integer n < –2. If there were, the equation could be multiplied through by
for integer n < –2. If there were, the equation could be multiplied through by 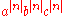 to obtain
to obtain 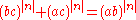 , which is impossible by Fermat's Last Theorem.
, which is impossible by Fermat's Last Theorem.Did Fermat possess a general proof?
The mathematical techniques used in Fermat's "marvelous" proof are unknown. Only one detailed proof of Fermat has survived, the above proof that no three coprime integers (x, y, z) satisfy the equation x4 − y4 = z4.Taylor and Wiles's proof relies on mathematical techniques developed in the twentieth century, which would be alien to mathematicians who had worked on Fermat's Last Theorem even a century earlier. Fermat's alleged "marvellous proof", by comparison, would have had to be elementary, given mathematical knowledge of the time, and so could not have been the same as Wiles' proof. Most mathematicians and science historians doubt that Fermat had a valid proof of his theorem for all exponents n.
Harvey Friedman
Harvey Friedman
Harvey Friedman is a mathematical logician at Ohio State University in Columbus, Ohio. He is noted especially for his work on reverse mathematics, a project intended to derive the axioms of mathematics from the theorems considered to be necessary...
's grand conjecture
Grand conjecture
In proof theory, a branch of mathematical logic, elementary function arithmetic or exponential function arithmetic is the system of arithmetic with the usual elementary properties of 0, 1, +, ×, xy, together with induction for formulas with bounded quantifiers.EFA is a...
implies that Fermat's last theorem can be proved in elementary arithmetic, a rather weak form of arithmetic with addition, multiplication, exponentiation, and a limited form of induction for formulas with bounded quantifiers. Any such proof would be elementary but possibly too long to write down.
Monetary prizes
In 1816 and again in 1850, the French Academy of SciencesFrench Academy of Sciences
The French Academy of Sciences is a learned society, founded in 1666 by Louis XIV at the suggestion of Jean-Baptiste Colbert, to encourage and protect the spirit of French scientific research...
offered a prize for a general proof of Fermat's Last Theorem. In 1857, the Academy awarded 3000 francs and a gold medal to Kummer for his research on ideal numbers, although he had not submitted an entry for the prize. Another prize was offered in 1883 by the Academy of Brussels.
In 1908, the German industrialist and amateur mathematician Paul Wolfskehl
Paul Wolfskehl
Paul Friedrich Wolfskehl , was an industrialist with an interest in mathematics. He bequeathed 100,000 marks to the first person to prove Fermat's Last Theorem.He was the younger of two sons of a rich Jewish banker, Joseph Carl Theodor Wolfskehl.His older brother, the jurist...
bequeathed 100,000 marks
Mark (money)
Mark was a measure of weight mainly for gold and silver, commonly used throughout western Europe and often equivalent to 8 ounces. Considerable variations, however, occurred throughout the Middle Ages Mark (from a merging of three Teutonic/Germanic languages words, Latinized in 9th century...
to the Göttingen Academy of Sciences to be offered as a prize for a complete proof of Fermat's Last Theorem. On 27 June 1908, the Academy published nine rules for awarding the prize. Among other things, these rules required that the proof be published in a peer-reviewed journal; the prize would not be awarded until two years after the publication; and that no prize would be given after 13 September 2007, roughly a century after the competition was begun. Wiles collected the Wolfskehl prize money, then worth $50,000, on 27 June 1997.
Prior to Wiles' proof, thousands of incorrect proofs were submitted to the Wolfskehl committee, amounting to roughly 10 feet (3 meters) of correspondence. In the first year alone (1907–1908), 621 attempted proofs were submitted, although by the 1970s, the rate of submission had decreased to roughly 3–4 attempted proofs per month. According to F. Schlichting, a Wolfskehl reviewer, most of the proofs were based on elementary methods taught in schools, and often submitted by "people with a technical education but a failed career". In the words of mathematical historian Howard Eves
Howard Eves
Howard Whitley Eves was an American mathematician, known for his work in geometry and the history of mathematics....
, "Fermat's Last Theorem has the peculiar distinction of being the mathematical problem for which the greatest number of incorrect proofs have been published."
In popular culture
- An episode in the television series Star Trek: The Next GenerationStar Trek: The Next GenerationStar Trek: The Next Generation is an American science fiction television series created by Gene Roddenberry as part of the Star Trek franchise. Roddenberry, Rick Berman, and Michael Piller served as executive producers at different times throughout the production...
, titled "The Royale", refers to the theorem in the first act. Riker visits Captain Jean-Luc Picard in his ready room to report only to find Picard puzzling over Fermat's last theorem. Picard's interest in this theorem goes beyond the difficulty of the puzzle; he also feels humbled that despite their advanced technology, they are still unable to solve a problem set forth by a man who had no computer. An episode in Star Trek: Deep Space 9, titled "Facets", refers to the theorem as well. In a scene involving O'Brien, Tobin Dax mentions continuing work on his own attempt to solve Fermat's last theorem.
- On August 17, 2011, a Google doodle was shown on the Google homepage, showing a blackboard with the theorem on it. When hovered over, it displays the text 'I have discovered a truly marvelous proof of this theorem, which this doodle is too small to contain.' This is a reference to the note made by Fermat in the margins of Arithmetica. It commemorated the 410th birth anniversary of Pierre de Fermat.
- In the book The Girl Who Played with FireThe Girl Who Played with FireThe Girl Who Played with Fire is the second novel in the best-selling "Millennium series" by Swedish writer Stieg Larsson. It was published posthumously in Swedish in 2006 and in English in January 2009....
, main character Lisbeth Salander becomes obsessed with the theorem in the opening chapters of the book. Her attempts to come up with a proof on her own is a running sub-plot throughout the story, and is used as a way to demonstrate her exceptional intelligence. In the end she ends up coming up with a proof (the actual proof is not featured in the book).
- In the Harold Ramis re-make of the movie "BedazzledBedazzled (2000 film)Bedazzled is a 2000 film remake of the 1967 film Bedazzled , originally written by Peter Cook and Dudley Moore, which was itself a comic retelling of the Faust legend...
," starring Brendan Fraser and Elizabeth Hurley, Fermat's Last Theorem appears written on the chalkboard in the classroom that the protagonist Elliot finds himself teleported to after he aborts his failed fourth wish. In the director's commentary for the DVD release, director Harold Ramis comments that nobody has seemed to notice that the equation on the board is Fermat's Last Theorem.
See also
- Euler's sum of powers conjecture
- Sophie Germain primeSophie Germain primeIn number theory, a prime number p is a Sophie Germain prime if 2p + 1 is also prime. For example, 23 is a Sophie Germain prime because it is a prime and 2 × 23 + 1 = 47, and 47 is also a prime number...
- Wall-Sun-Sun primeWall-Sun-Sun primeIn number theory, a Wall–Sun–Sun prime or Fibonacci–Wieferich prime is a certain kind of prime number which is conjectured to exist although none are known.- Definition :...
- Beal's conjectureBeal's conjectureBeal's conjecture is a conjecture in number theory proposed by Andrew Beal in about 1993; a similar conjecture was suggested independently at about the same time by Andrew Granville....
- Fermat's Last Theorem in fictionFermat's Last Theorem in fictionThe famous problem in number theory known as "Fermat's Last Theorem" has repeatedly received attention in fiction and popular culture.* In the Doctor Who episode "The Eleventh Hour", the Doctor provides "the real" proof of Fermat's theorem to show his bona fides.* In "The Royale", an episode of...
- Diophantus II.VIIIDiophantus II.VIIIThe eighth problem of the second book of Diophantus's Arithmetica is to divide a square into a sum of two squares.-The solution given by Diophantus:Diophantus takes the square to be 16 and solves the problem as follows:...
External links
- The bluffer's guide to Fermat's Last Theorem Blog that covers the history of Fermat's Last Theorem from Fermat to Wiles. Discusses various material which is related to the proof of Fermat's Last Theorem: elliptic curves, modular forms, Galois representations and their deformations, Frey's construction, and the conjectures of Serre and of Taniyama–Shimura. The story, the history and the mystery. The title of one edition of the PBS television series NOVA, discusses Andrew Wiles's effort to prove Fermat's Last Theorem. Simon Singh and John Lynch's film tells the story of Andrew Wiles.

