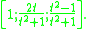The eighth problem of the second book of Diophantus

Diophantus

Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...

's Arithmetica

Arithmetica

Arithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...

 is to divide a square into a sum of two squares.

The solution given by Diophantus

Diophantus takes the square to be 16 and solves the problem as follows:

To divide a given square into a sum of two squares.

To divide 16 into a sum of two squares.

Let the first summand be , and thus the second . The latter is to be a square. I form the square of the difference of an arbitrary multiple of x diminished by the root [of] 16, that is, diminished by 4. I form, for example, the square of 2x − 4. It is . I put this expression equal to . I add to both sides and subtract 16. In this way I obtain , hence .

Thus one number is 256/25 and the other 144/25. The sum of these numbers is 16 and each summand is a square.

Geometrical interpretation

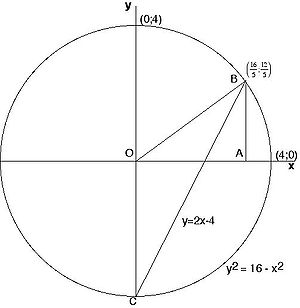
Geometrically, we may illustrate this method by drawing the circle x² + y² = 4² and the line y = 2x - 4. The pair of squares sought are then x₀² and y₀², where (x₀, y₀) is the point not on the y-axis where the line and circle intersect. This is shown in the diagram to the right.

Generalization of Diophantus's solution

We may generalize Diophantus's solution to solve the problem for any given square, which we will represent algebraically as a². Also, since Diophantus

Diophantus

Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...

 refers to an arbitrary multiple of x, we will take the arbitrary multiple to be tx. Then:

Therefore, we find that one of the summands is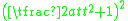 and the other is 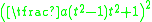. The sum of these numbers is 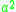and each summand is a square. Geometrically, we have intersected the circle x² + y² = a² with the line y = tx - a, as shown in the diagram to the right. Writing the lengths, OB, OA, and AB, of the sides of triangle OAB as an ordered tuple, we obtain the triple.


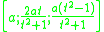The specific result obtained by Diophantus may be obtained by taking a = 4 and t = 2: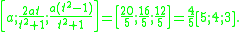
We see that Diophantus' particular solution is in fact a subtly disguised (3, 4, 5) triple. However, as the triple will always be rational as long as a and t are rational, we can obtain an infinity of rational triples by changing the value of t, and hence changing the value of the arbitrary multiple of x.

This algebraic solution needs only one additional step to arrive at the Platonic sequence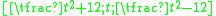  and that is to multiply all sides of the above triple by a factor 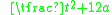. Notice also that if a = 1, the sides [OB, OA, AB] reduce to

In modern notation this is just written in terms of the cotangent of θ/2, which in the particular example given by Diophantus has a value of 2, the multiplier in the arbitrary multiple of x. Upon clearing denominators, this expression will generate Pythagorean triple

Pythagorean triple

A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...

s. Intriguingly, the arbitrary multiple of x has become the cornerstone of the generator expression(s).

Diophantus II.IX reaches the same solution by an even quicker route which is very similar to the 'generalized solution' above. Once again the problem is to divide 16 into two squares.

Let the first number be N and the second an arbitrary multiple of N diminished by the root (of) 16. For example 2N − 4. Then:

Historical note: Fermat's

Pierre de Fermat

Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...

 famous comment which later became Fermat's Last Theorem

Fermat's Last Theorem

In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....

 appears sandwiched between 'Quaestio VIII' and 'Quaestio IX' on page 61 of a 1670 edition of Arithmetica.

See also

• Pythagorean triple
  Pythagorean triple
  A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
  
  
• Fermat's Last Theorem and Diophantus II.VIII

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.