Kummer ring
Encyclopedia
In abstract algebra
, a Kummer ring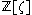
is a subring
of the ring
of complex numbers, such that each of its elements has the form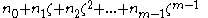
where ζ is an mth root of unity
, i.e.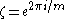
and n0 through nm-1 are integer
s.
A Kummer ring is an extension of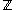
, the ring of integers
, hence the symbol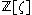
. Since the minimal polynomial of ζ is the m-th cyclotomic polynomial
, the ring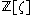
is an extension of degree 
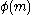(where φ denotes Euler's totient function
).
An attempt to visualize a Kummer ring on an Argand diagram
might yield something resembling a quaint Renaissance map with compass rose
s and rhumb line
s.
The set of units
of a Kummer ring contains
.
By Dirichlet's unit theorem
, there are also units of infinite order,
except in the cases m=1, m=2 (in which case we have the ordinary ring of integer
s), the case m=4 (the Gaussian integer
s) and the cases m=3, m=6 (the Eisenstein integer
s).
Kummer rings are named after Ernst Kummer
, who studied the unique factorization of their elements.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a Kummer ring
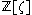is a subringSubring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of complex numbers, such that each of its elements has the form
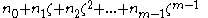
where ζ is an mth root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, i.e.
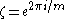
and n0 through nm-1 are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s.
A Kummer ring is an extension of
, the ring of integersRing of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
, hence the symbol
. Since the minimal polynomial of ζ is the m-th cyclotomic polynomialCyclotomic polynomial
In algebra, the nth cyclotomic polynomial, for any positive integer n, is the monic polynomial:\Phi_n = \prod_\omega \,where the product is over all nth primitive roots of unity ω in a field, i.e...
, the ring
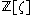is an extension of degree 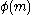(where φ denotes Euler's totient functionEuler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
).
An attempt to visualize a Kummer ring on an Argand diagram
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
might yield something resembling a quaint Renaissance map with compass rose
Compass rose
A compass rose, sometimes called a windrose, is a figure on a compass, map, nautical chart or monument used to display the orientation of the cardinal directions — North, East, South and West - and their intermediate points. It is also the term for the graduated markings found on the traditional...
s and rhumb line
Rhumb line
In navigation, a rhumb line is a line crossing all meridians of longitude at the same angle, i.e. a path derived from a defined initial bearing...
s.
The set of units
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
of a Kummer ring contains
.By Dirichlet's unit theorem
Dirichlet's unit theorem
In mathematics, Dirichlet's unit theorem is a basic result in algebraic number theory due to Gustav Lejeune Dirichlet. It determines the rank of the group of units in the ring OK of algebraic integers of a number field K...
, there are also units of infinite order,
except in the cases m=1, m=2 (in which case we have the ordinary ring of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s), the case m=4 (the Gaussian integer
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s) and the cases m=3, m=6 (the Eisenstein integer
Eisenstein integer
In mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
s).
Kummer rings are named after Ernst Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
, who studied the unique factorization of their elements.