
Cluster decomposition theorem
Encyclopedia
In physics
, the cluster decomposition theorem guarantees locality
in quantum field theory
. According to this theorem
, the vacuum expectation value
of a product of many operators - each of them being either in region A or in region B where A and B are very separated - asymptotically equals the product of the expectation value of the product of the operators in A, times a similar factor from the region B. Consequently, sufficiently separated regions behave independently.
If A1, ..., An are n operators each localized in a bounded region and U(a) represents the unitary operator
actively translating the Hilbert space by the vector a, then if we pick some subset of the n operators to translate,
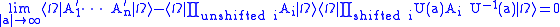
where |Ω> is the vacuum state
, and
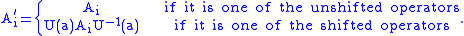
provided a is a spacelike vector.
Expressed in terms of the connected correlation functions, it means if some of the arguments of the connected correlation function are shifted by large spacelike separations, the function goes to zero.
This theorem only holds if the vacuum is a pure state. If the vacuum is degenerate
and we have a mixed state, the cluster decomposition theorem fails.
If the theory has a mass gap
m>0, then there is a value a0 beyond which the connected correlation function is absolutely bounded by c e-m|a| where c is some coefficient and |a| is the length of the vector a for |a|>a0.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the cluster decomposition theorem guarantees locality
Principle of locality
In physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Experiments have shown that quantum mechanically entangled particles must violate either the principle of locality or the form of philosophical realism known as counterfactual...
in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. According to this theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
, the vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of a product of many operators - each of them being either in region A or in region B where A and B are very separated - asymptotically equals the product of the expectation value of the product of the operators in A, times a similar factor from the region B. Consequently, sufficiently separated regions behave independently.
If A1, ..., An are n operators each localized in a bounded region and U(a) represents the unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
actively translating the Hilbert space by the vector a, then if we pick some subset of the n operators to translate,
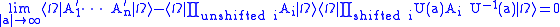
where |Ω> is the vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
, and
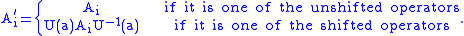
provided a is a spacelike vector.
Expressed in terms of the connected correlation functions, it means if some of the arguments of the connected correlation function are shifted by large spacelike separations, the function goes to zero.
This theorem only holds if the vacuum is a pure state. If the vacuum is degenerate
Degeneracy
Degeneracy may refer to:* DegenerationIn science and mathematics:* Degeneracy , a property of quantum states sharing the same energy levels...
and we have a mixed state, the cluster decomposition theorem fails.
If the theory has a mass gap
Mass gap
In quantum field theory, the mass gap is the difference in energy between the vacuum and the next lowest energy state. The energy of the vacuum is zero by definition, and assuming that all energy states can be thought of as particles in plane-waves, the mass gap is the mass of the lightest...
m>0, then there is a value a0 beyond which the connected correlation function is absolutely bounded by c e-m|a| where c is some coefficient and |a| is the length of the vector a for |a|>a0.

