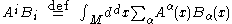DeWitt notation
Encyclopedia
Physics often deals with classical models where the dynamical variables are a collection of functions
{φα}α over a d-dimensional space/spacetime manifold
M where α is the "flavor" index. This involves functional
s over the φs, functional derivative
s, functional integrals, etc. From a functional point of view this is equivalent to working with an infinite-dimensional smooth manifold where its points are an assignment of a function for each α, and the procedure is in analogy with differential geometry where the coordinates for a point x of the manifold M are φα(x).
In the DeWitt notation (named after theoretical physicist Bryce DeWitt
), φα(x) is written as φi where i is now understood as an index covering both α and x.
So, given a smooth functional A, A,i stands for the functional derivative
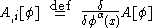
as a functional of φ. In other words, a "1-form" field over the infinite dimensional "functional manifold".
In integrals, the Einstein summation convention is used. Alternatively,
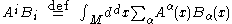
{φα}α over a d-dimensional space/spacetime manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M where α is the "flavor" index. This involves functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
s over the φs, functional derivative
Functional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
s, functional integrals, etc. From a functional point of view this is equivalent to working with an infinite-dimensional smooth manifold where its points are an assignment of a function for each α, and the procedure is in analogy with differential geometry where the coordinates for a point x of the manifold M are φα(x).
In the DeWitt notation (named after theoretical physicist Bryce DeWitt
Bryce DeWitt
Bryce Seligman DeWitt was a theoretical physicist renowned for advancing gravity and field theories.-Biography:...
), φα(x) is written as φi where i is now understood as an index covering both α and x.
So, given a smooth functional A, A,i stands for the functional derivative
Functional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
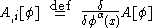
as a functional of φ. In other words, a "1-form" field over the infinite dimensional "functional manifold".
In integrals, the Einstein summation convention is used. Alternatively,