
Drag equation
Encyclopedia
In fluid dynamics
, the drag equation is a practical formula used to calculate the force of drag
experienced by an object due to movement through a fully enclosing fluid
.
The equation is attributed to Lord Rayleigh, who originally used L2 in place of A (with L being some linear dimension).
But see Section 7 of Book 2 of Newton's Principia Mathematica
; in particular Proposition 37.
The force on a moving object due to a fluid is:
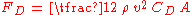
where
The reference area A is typically defined as the area of the orthographic projection
of the object on a plane perpendicular to the direction of motion. For non-hollow objects with simple shape, such as a sphere, this is exactly the same as a cross sectional
area. For other objects (for instance, a rolling tube or the body of a cyclist), A may be significantly larger than the area of any cross section along any plane perpendicular to the direction of motion. Airfoils use the square of the chord length
as the reference area; since airfoil chords are usually defined with a length of 1, the reference area is also 1. Aircraft use the wing area (or rotor-blade area) as the reference area, which makes for an easy comparison to lift
. Airships
and bodies of revolution
use the volumetric coefficient of drag, in which the reference area is the square of the cube root of the airship's volume. Sometimes different reference areas are given for the same object in which case a drag coefficient corresponding to each of these different areas must be given.
For sharp-cornered bluff bodies, like square cylinders and plates held transverse to the flow direction, this equation is applicable with the drag coefficient as a constant value when the Reynolds number is greater than 1000. For smooth bodies, like a circular cylinder, the drag coefficient may vary significantly until Reynolds numbers up to 107 (ten million).
), which varies with the Reynolds number and is found by experiment.
Of particular importance is the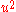 dependence on velocity, meaning that fluid drag increases with the square of velocity. When velocity is doubled, for example, not only does the fluid strike with twice the velocity, but twice the mass
dependence on velocity, meaning that fluid drag increases with the square of velocity. When velocity is doubled, for example, not only does the fluid strike with twice the velocity, but twice the mass
of fluid strikes per second. Therefore the change of momentum
per second is multiplied by four. Force
is equivalent to the change of momentum divided by time. This is in contrast with solid-on-solid friction
, which generally has very little velocity dependence.
The drag equation may be derived to within a multiplicative constant by the method of dimensional analysis
. If a moving fluid meets an object, it exerts a force on the object, according to a complicated (and not completely understood) law. We might suppose that the variables involved under some conditions to be the:
Using the algorithm of the Buckingham π theorem, one can reduce these five variables to two dimensionless parameters:
Alternatively, one can derive the dimensionless parameters via direct manipulation of the underlying differential equations.
That this is so becomes apparent when the drag force FD is expressed as part of a function of the other variables in the problem:
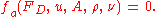
This rather odd form of expression is used because it does not assume a one-to-one relationship. Here, fa is some (as-yet-unknown) function that takes five arguments. We note that the right-hand side is zero in any system of units; so it should be possible to express the relationship described by fa in terms of only dimensionless groups.
There are many ways of combining the five arguments of fa to form dimensionless groups, but the Buckingham π theorem states that there will be two such groups. The most appropriate are the Reynolds number, given by
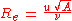
and the drag coefficient, given by
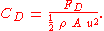
Thus the function of five variables may be replaced by another function of only two variables:
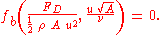
where fb is some function of two arguments.
The original law is then reduced to a law involving only these two numbers.
Because the only unknown in the above equation is the drag force FD, it is possible to express it as
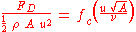
or
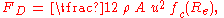 and with
and with 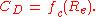
Thus the force is simply ½ ρ A u2 times some (as-yet-unknown) function fc of the Reynolds number Re — a considerably simpler system than the original five-argument function given above.
Dimensional analysis thus makes a very complex problem (trying to determine the behavior of a function of five variables) a much simpler one: the determination of the drag as a function of only one variable, the Reynolds number.
The analysis also gives other information for free, so to speak. We know that, other things being equal, the drag force will be proportional to the density of the fluid. This kind of information often proves to be extremely valuable, especially in the early stages of a research project.
To empirically determine the Reynolds number dependence, instead of experimenting on huge bodies with fast-flowing fluids (such as real-size airplanes in wind-tunnels), one may just as well experiment on small models with more viscous and higher velocity fluids, because these two systems are similar
.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the drag equation is a practical formula used to calculate the force of drag
Drag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
experienced by an object due to movement through a fully enclosing fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
.
The equation is attributed to Lord Rayleigh, who originally used L2 in place of A (with L being some linear dimension).
But see Section 7 of Book 2 of Newton's Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
; in particular Proposition 37.
The force on a moving object due to a fluid is:
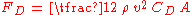
where
- FD is the forceForceIn physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
of drag, which is by definition the force component in the direction of the flow velocity, - ρ is the mass density of the fluid,
- v is the velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the object relative to the fluid, - A is the reference areaAreaArea is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
, and - CD is the drag coefficientDrag coefficientIn fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment such as air or water. It is used in the drag equation, where a lower drag coefficient indicates the object will have less aerodynamic or...
— a dimensionless constantCoefficientIn mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
related to the object's geometry and taking into account both skin friction and form drag.
The reference area A is typically defined as the area of the orthographic projection
Orthographic projection
Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface...
of the object on a plane perpendicular to the direction of motion. For non-hollow objects with simple shape, such as a sphere, this is exactly the same as a cross sectional
Cross section (geometry)
In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...
area. For other objects (for instance, a rolling tube or the body of a cyclist), A may be significantly larger than the area of any cross section along any plane perpendicular to the direction of motion. Airfoils use the square of the chord length
Chord (aircraft)
In aeronautics, chord refers to the imaginary straight line joining the trailing edge and the center of curvature of the leading edge of the cross-section of an airfoil...
as the reference area; since airfoil chords are usually defined with a length of 1, the reference area is also 1. Aircraft use the wing area (or rotor-blade area) as the reference area, which makes for an easy comparison to lift
Lift (force)
A fluid flowing past the surface of a body exerts a surface force on it. Lift is the component of this force that is perpendicular to the oncoming flow direction. It contrasts with the drag force, which is the component of the surface force parallel to the flow direction...
. Airships
Airship
An airship or dirigible is a type of aerostat or "lighter-than-air aircraft" that can be steered and propelled through the air using rudders and propellers or other thrust mechanisms...
and bodies of revolution
Solid of revolution
In mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane....
use the volumetric coefficient of drag, in which the reference area is the square of the cube root of the airship's volume. Sometimes different reference areas are given for the same object in which case a drag coefficient corresponding to each of these different areas must be given.
For sharp-cornered bluff bodies, like square cylinders and plates held transverse to the flow direction, this equation is applicable with the drag coefficient as a constant value when the Reynolds number is greater than 1000. For smooth bodies, like a circular cylinder, the drag coefficient may vary significantly until Reynolds numbers up to 107 (ten million).
Discussion
The equation is based on an idealized situation where all of the fluid impinges on the reference area and comes to a complete stop, building up stagnation pressure over the whole area. No real object exactly corresponds to this behavior. CD is the ratio of drag for any real object to that of the ideal object. In practice a rough unstreamlined body (a bluff body) will have a CD around 1, more or less. Smoother objects can have much lower values of CD. The equation is precise — it simply provides the definition of CD (drag coefficientDrag coefficient
In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment such as air or water. It is used in the drag equation, where a lower drag coefficient indicates the object will have less aerodynamic or...
), which varies with the Reynolds number and is found by experiment.
Of particular importance is the
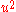 dependence on velocity, meaning that fluid drag increases with the square of velocity. When velocity is doubled, for example, not only does the fluid strike with twice the velocity, but twice the mass
dependence on velocity, meaning that fluid drag increases with the square of velocity. When velocity is doubled, for example, not only does the fluid strike with twice the velocity, but twice the massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of fluid strikes per second. Therefore the change of momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
per second is multiplied by four. Force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
is equivalent to the change of momentum divided by time. This is in contrast with solid-on-solid friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
, which generally has very little velocity dependence.
Derivation
The drag equation may be derived to within a multiplicative constant by the method of dimensional analysis
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
. If a moving fluid meets an object, it exerts a force on the object, according to a complicated (and not completely understood) law. We might suppose that the variables involved under some conditions to be the:
- speed u,
- fluid density ρ,
- viscosity ν of the fluid,
- size of the body, expressed in terms of its frontal area A, and
- drag force FD.
Using the algorithm of the Buckingham π theorem, one can reduce these five variables to two dimensionless parameters:
- drag coefficientDrag coefficientIn fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment such as air or water. It is used in the drag equation, where a lower drag coefficient indicates the object will have less aerodynamic or...
CD and - Reynolds number Re.
Alternatively, one can derive the dimensionless parameters via direct manipulation of the underlying differential equations.
That this is so becomes apparent when the drag force FD is expressed as part of a function of the other variables in the problem:
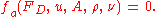
This rather odd form of expression is used because it does not assume a one-to-one relationship. Here, fa is some (as-yet-unknown) function that takes five arguments. We note that the right-hand side is zero in any system of units; so it should be possible to express the relationship described by fa in terms of only dimensionless groups.
There are many ways of combining the five arguments of fa to form dimensionless groups, but the Buckingham π theorem states that there will be two such groups. The most appropriate are the Reynolds number, given by
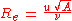
and the drag coefficient, given by
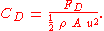
Thus the function of five variables may be replaced by another function of only two variables:
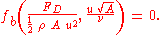
where fb is some function of two arguments.
The original law is then reduced to a law involving only these two numbers.
Because the only unknown in the above equation is the drag force FD, it is possible to express it as
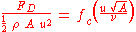
or
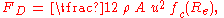 and with
and with 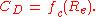
Thus the force is simply ½ ρ A u2 times some (as-yet-unknown) function fc of the Reynolds number Re — a considerably simpler system than the original five-argument function given above.
Dimensional analysis thus makes a very complex problem (trying to determine the behavior of a function of five variables) a much simpler one: the determination of the drag as a function of only one variable, the Reynolds number.
The analysis also gives other information for free, so to speak. We know that, other things being equal, the drag force will be proportional to the density of the fluid. This kind of information often proves to be extremely valuable, especially in the early stages of a research project.
To empirically determine the Reynolds number dependence, instead of experimenting on huge bodies with fast-flowing fluids (such as real-size airplanes in wind-tunnels), one may just as well experiment on small models with more viscous and higher velocity fluids, because these two systems are similar
Similitude (model)
Similitude is a concept applicable to the testing of engineering models. A model is said to have similitude with the real application if the two share geometric similarity, kinematic similarity and dynamic similarity...
.
See also
- Aerodynamic drag
- Angle of attackAngle of attackAngle of attack is a term used in fluid dynamics to describe the angle between a reference line on a lifting body and the vector representing the relative motion between the lifting body and the fluid through which it is moving...
- Drag (physics)Drag (physics)In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
- Morison equationMorison equationIn fluid dynamics the Morison equation is a semi-empirical equation for the inline force on a body in oscillatory flow. It is sometimes called the MOJS equation after all four authors—Morison, O'Brien, Johnson and Schaaf—of the 1950 paper in which the equation was introduced...
- Stall (flight)Stall (flight)In fluid dynamics, a stall is a reduction in the lift coefficient generated by a foil as angle of attack increases. This occurs when the critical angle of attack of the foil is exceeded...
- Terminal velocityTerminal velocityIn fluid dynamics an object is moving at its terminal velocity if its speed is constant due to the restraining force exerted by the fluid through which it is moving....

