
Morison equation
Encyclopedia
In fluid dynamics
the Morison equation is a semi-empirical
equation for the inline force on a body in oscillatory flow. It is sometimes called the MOJS equation after all four authors—Morison, O'Brien, Johnson and Schaaf—of the 1950 paper in which the equation was introduced. The Morison equation is used to estimate the wave
loads in the design of oil platform
s and other offshore structures
.
force in phase with the local flow acceleration
and a drag
force proportional to the (signed) square of the instantaneous flow velocity
. The inertia force is of the functional form as found in potential flow
theory, while the drag force has the form as found for a body placed in a steady flow. In the heuristic
approach of Morison, O'Brien, Johnson and Schaaf these two force components, inertia and drag, are simply added to describe the force in an oscillatory flow.
The Morison equation contains two empirical hydrodynamic coefficients—an inertia coefficient and a drag coefficient
—which are determined from experimental data. As shown by dimensional analysis
and in experiments by Sarpkaya, these coefficients depend in general on the Keulegan–Carpenter number
, Reynolds number and surface roughness.
The descriptions given below of the Morison equation are for uni-directional onflow conditions as well as body motion.
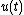 , the Morison equation gives the inline force parallel to the flow direction:
, the Morison equation gives the inline force parallel to the flow direction:
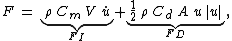
where
For instance for a circular cylinder of diameter D in oscillatory flow, the reference area per unit cylinder length is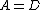 and the cylinder volume per unit cylinder length is
and the cylinder volume per unit cylinder length is 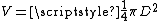 . As a result,
. As a result,  is the total force per unit cylinder length:
is the total force per unit cylinder length:
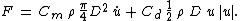
Besides the inline force, there are also oscillatory lift
forces perpendicular to the flow direction, due to vortex shedding
. These are not covered by the Morison equation, which is only for the inline forces.
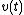 , the Morison equation becomes:
, the Morison equation becomes:
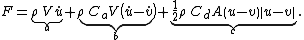
where the total force contributions are:
Note that the added mass coefficient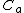 is related to the inertia coefficient
is related to the inertia coefficient 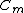 as
as 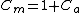 .
.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
the Morison equation is a semi-empirical
Empirical
The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....
equation for the inline force on a body in oscillatory flow. It is sometimes called the MOJS equation after all four authors—Morison, O'Brien, Johnson and Schaaf—of the 1950 paper in which the equation was introduced. The Morison equation is used to estimate the wave
Ocean surface wave
In fluid dynamics, wind waves or, more precisely, wind-generated waves are surface waves that occur on the free surface of oceans, seas, lakes, rivers, and canals or even on small puddles and ponds. They usually result from the wind blowing over a vast enough stretch of fluid surface. Waves in the...
loads in the design of oil platform
Oil platform
An oil platform, also referred to as an offshore platform or, somewhat incorrectly, oil rig, is a lаrge structure with facilities to drill wells, to extract and process oil and natural gas, and to temporarily store product until it can be brought to shore for refining and marketing...
s and other offshore structures
Offshore construction
Offshore construction is the installation of structures and facilities in a marine environment, usually for the production and transmission of electricity, oil, gas and other resources....
.
Description
The Morison equation is the sum of two force components: an inertiaInertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
force in phase with the local flow acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
and a drag
Drag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
force proportional to the (signed) square of the instantaneous flow velocity
Flow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
. The inertia force is of the functional form as found in potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
theory, while the drag force has the form as found for a body placed in a steady flow. In the heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
approach of Morison, O'Brien, Johnson and Schaaf these two force components, inertia and drag, are simply added to describe the force in an oscillatory flow.
The Morison equation contains two empirical hydrodynamic coefficients—an inertia coefficient and a drag coefficient
Drag coefficient
In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment such as air or water. It is used in the drag equation, where a lower drag coefficient indicates the object will have less aerodynamic or...
—which are determined from experimental data. As shown by dimensional analysis
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
and in experiments by Sarpkaya, these coefficients depend in general on the Keulegan–Carpenter number
Keulegan–Carpenter number
In fluid dynamics, the Keulegan–Carpenter number, also called the period number, is a dimensionless quantity describing the relative importance of the drag forces over inertia forces for bluff objects in an oscillatory fluid flow. Or similarly, for objects that oscillate in a fluid at rest...
, Reynolds number and surface roughness.
The descriptions given below of the Morison equation are for uni-directional onflow conditions as well as body motion.
Fixed body in an oscillatory flow
In an oscillatory flow with flow velocityFlow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
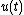 , the Morison equation gives the inline force parallel to the flow direction:
, the Morison equation gives the inline force parallel to the flow direction: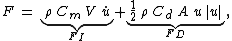
where
-
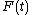 is the total inline force on the object,
is the total inline force on the object, -
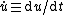 is the flow acceleration, i.e. the time derivativeTime derivativeA time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as t\,.-Notation:...
is the flow acceleration, i.e. the time derivativeTime derivativeA time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as t\,.-Notation:...
of the flow velocity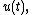
- the inertia force
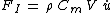 , is the sum of the Froude–Krylov force
, is the sum of the Froude–Krylov force  and the hydrodynamic mass force
and the hydrodynamic mass force 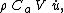
- the drag force
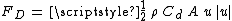 ,
, -
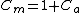 is the inertia coefficient, and
is the inertia coefficient, and 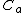 the added massAdded massIn fluid mechanics, added mass or virtual mass is the inertia added to a system because an accelerating or decelerating body must move some volume of surrounding fluid as it moves through it, since the object and fluid cannot occupy the same physical space simultaneously...
the added massAdded massIn fluid mechanics, added mass or virtual mass is the inertia added to a system because an accelerating or decelerating body must move some volume of surrounding fluid as it moves through it, since the object and fluid cannot occupy the same physical space simultaneously...
coefficient, - A is a reference area, e.g. the cross-sectional area of the body perpendicular to the flow direction,
- V is volume of the body.
For instance for a circular cylinder of diameter D in oscillatory flow, the reference area per unit cylinder length is
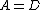 and the cylinder volume per unit cylinder length is
and the cylinder volume per unit cylinder length is 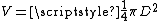 . As a result,
. As a result,  is the total force per unit cylinder length:
is the total force per unit cylinder length: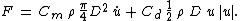
Besides the inline force, there are also oscillatory lift
Lift (force)
A fluid flowing past the surface of a body exerts a surface force on it. Lift is the component of this force that is perpendicular to the oncoming flow direction. It contrasts with the drag force, which is the component of the surface force parallel to the flow direction...
forces perpendicular to the flow direction, due to vortex shedding
Vortex shedding
Vortex shedding is an unsteady flow that takes place in special flow velocities . In this flow, vortices are created at the back of the body and detach periodically from either side of the body. See Von Kármán vortex street.Vortex shedding is caused when a fluid flows past a blunt object...
. These are not covered by the Morison equation, which is only for the inline forces.
Moving body in an oscillatory flow
In case the body moves as well, with velocity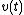 , the Morison equation becomes:
, the Morison equation becomes: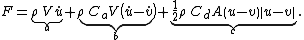
where the total force contributions are:
- a: Froude–Krylov force,
- b: hydrodynamic mass force,
- c: drag force.
Note that the added mass coefficient
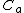 is related to the inertia coefficient
is related to the inertia coefficient 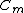 as
as 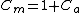 .
.Limitations
- The Morison equation is a heuristic formulation of the force fluctuations in an oscillatory flow. The first assumption is that the flow acceleration is more-or-less uniform at the location of the body. For instance, for a vertical cylinder in surface gravity wavesOcean surface waveIn fluid dynamics, wind waves or, more precisely, wind-generated waves are surface waves that occur on the free surface of oceans, seas, lakes, rivers, and canals or even on small puddles and ponds. They usually result from the wind blowing over a vast enough stretch of fluid surface. Waves in the...
this requires that the diameter of the cylinder is much smaller than the wavelengthWavelengthIn physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
. If the diameter of the body is not small compared to the wavelength, diffractionDiffractionDiffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
effects have to be taken into account. - Second, it is assumed that the asymptotic forms: the inertia and drag force contributions, valid for very small and very large Keulegan–Carpenter numbers respectively, can just be added to describe the force fluctuations at intermediate Keulegan–Carpenter numbers. However, from experiments it is found that in this intermediate regime—where both drag and inertia are giving significant contributions—the Morison equation is not capable to describe the force history very well. Although the inertia and drag coefficients can be tuned to give the correct extreme values of the force.
- Third, when extended to orbital flow which is a case of non uni-directional flow, for instance encountered by a horizontal cylinder under waves, the Morison equation does not give a good representation of the forces as a function of time.

