
Demagnetizing field
Encyclopedia
The demagnetizing field, also called the stray field, is the magnetic field
(H-field) generated by the magnetization
in a magnet
. The total magnetic field in a region containing magnets is the sum of the demagnetizing fields of the magnets and the magnetic field due to any free currents or displacement current
s. The term demagnetizing field reflects its tendency to act on the magnetization so as to reduce the total magnetic moment
. It gives rise to shape anisotropy in ferromagnets with a single magnetic domain and to magnetic domains
in larger ferromagnets.
The demagnetizing field of an arbitrary shaped object is very difficult to calculate even for the simple case of uniform magnetization. For the special case of ellipsoids (which includes sphere
s) the demagnetization field is linearly related to the magnetization by a geometry dependent constant called the demagnetizing factor. Since the magnetization of a sample at a given location depends on the total magnetic field at that point, the demagnetization factor must be used in order to accurately determine how a magnetic material responds to a magnetic field. (See magnetic hysteresis.)
for a body with no electric currents. These are Ampère's law
and Gauss's law
The magnetic field and flux density are related by
of a scalar
potential
:
Inside the magnetic body, the potential is determined by substituting and in :
Outside the body, where the magnetization is zero,
At the surface of the magnet, there are two continuity requirements:
This leads to the following boundary conditions at the surface of the magnet:
Here is the surface normal
and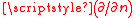 is the derivative with respect to distance from the surface.
is the derivative with respect to distance from the surface.
The outer potential must also be regular at infinity: both and must be bounded as goes to infinity. This ensures that the magnetic energy is finite. Sufficiently far away, the magnetic field looks like the field of a magnetic dipole
with the same moment
as the finite body.
Suppose there are two magnets with magnetizations and . The energy of the first magnet in the demagnetizing field of the second is
The reciprocity theorem states that
where is the variable to be integrated over the volume of the body in the first integral and the surface in the second, and is the gradient with respect to this variable.
Qualitatively, the negative of the divergence of the magnetization (called a volume pole) is analogous to a bulk bound electric charge in the body while (called a surface pole) is analogous to a bound surface electric charge. Although the magnetic charges do not exist, it can be useful to think of them in this way. In particular, the arrangement of magnetization that reduces the magnetic energy can often be understood in terms of the pole-avoidance principle, which states that the magnetization tries to reduce the poles as much as possible.
File:SingleDomainMagneticCharges.svg|thumb|right|Illustration of the magnetic charges at the surface of a single-domain ferromagnet. The arrows indicate the direction of magnetization. The thickness of the colored region indicates the surface charge density.
default direct SVG link
One way to remove the magnetic poles inside a ferromagnet is to make the magnetization uniform. This occurs in single-domain ferromagnets. This still leaves the surface poles, so division into domains
reduces the poles further. However, very small ferromagnets are kept uniformly magnetized by the exchange interaction
.
The concentration of poles depends on the direction of magnetization (see the figure). If the magnetization is along the longest axis, the poles are spread across a smaller surface, so the energy is lower. This is a form of magnetic anisotropy
called shape anisotropy.
. It is then possible to have the magnetization parallel to the surface. Within each domain the magnetization is uniform, so there are no volume poles, but there are surface poles at the interfaces (domain walls) between domains. However, these poles vanish if the magnetic moments on each side of the domain wall meet the wall at the same angle (so that the components are the same but opposite in sign). Domains configured this way are called closure domains.
where is the magnetization of the sphere and is called the demagnetizing factor and equals for a sphere.
This equation can be generalized to include ellipsoids having principal axes in x,y, and z directions such that each component has a relationship of the form:
Other important examples are an infinite plate (an ellipsoid with two of its axes going to infinity) which has = in a direction normal to the plate and zero otherwise and an infinite cylinder (an ellipsoid with one of its axes tending toward infinity with the other two being the same) which has = along its axis. For tables or equations for the magnetizing factors of the general ellipsoid see .
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
(H-field) generated by the magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
in a magnet
Magnet
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, and attracts or repels other magnets.A permanent magnet is an object...
. The total magnetic field in a region containing magnets is the sum of the demagnetizing fields of the magnets and the magnetic field due to any free currents or displacement current
Displacement current
In electromagnetism, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do. However it is not an electric...
s. The term demagnetizing field reflects its tendency to act on the magnetization so as to reduce the total magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
. It gives rise to shape anisotropy in ferromagnets with a single magnetic domain and to magnetic domains
Magnetic domains
A magnetic domain describes a region within a magnetic material which has uniform magnetization. This means that the individual magnetic moments of the atoms are aligned with one another and they point in the same direction...
in larger ferromagnets.
The demagnetizing field of an arbitrary shaped object is very difficult to calculate even for the simple case of uniform magnetization. For the special case of ellipsoids (which includes sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s) the demagnetization field is linearly related to the magnetization by a geometry dependent constant called the demagnetizing factor. Since the magnetization of a sample at a given location depends on the total magnetic field at that point, the demagnetization factor must be used in order to accurately determine how a magnetic material responds to a magnetic field. (See magnetic hysteresis.)
Maxwell's equations
In general the demagnetizing field is a function of position . It is derived from the magnetostatic equationsMagnetostatics
Magnetostatics is the study of magnetic fields in systems where the currents are steady . It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching events that...
for a body with no electric currents. These are Ampère's law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
and Gauss's law
The magnetic field and flux density are related by
The magnetic potential
The general solution of the first equation can be expressed as the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a scalar
Scalar
Scalar may refer to:*Scalar , a quantity used to multiply vectors in the context of vector spaces*Scalar , a quantity which is independent of specific classes of coordinate systems...
potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
:
Inside the magnetic body, the potential is determined by substituting and in :
Outside the body, where the magnetization is zero,
At the surface of the magnet, there are two continuity requirements:
- The component of parallelParallel (geometry)Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
to the surface must be continuous (no jump in value at the surface). - The component of perpendicularPerpendicularIn geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the surface must be continuous.
This leads to the following boundary conditions at the surface of the magnet:
Here is the surface normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
and
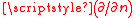 is the derivative with respect to distance from the surface.
is the derivative with respect to distance from the surface.The outer potential must also be regular at infinity: both and must be bounded as goes to infinity. This ensures that the magnetic energy is finite. Sufficiently far away, the magnetic field looks like the field of a magnetic dipole
Magnetic dipole
A magnetic dipole is the limit of either a closed loop of electric current or a pair of poles as the dimensions of the source are reduced to zero while keeping the magnetic moment constant. It is a magnetic analogue of the electric dipole, but the analogy is not complete. In particular, a magnetic...
with the same moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
as the finite body.
Uniqueness of the demagnetizing field
Any two potentials that satisfy equations , and , along with regularity at infinity, are identical. The demagnetizing field is the gradient of this potential (equation ).Energy
The energy of the demagnetizing field is completely determined by an integral over the volume of the magnet:Suppose there are two magnets with magnetizations and . The energy of the first magnet in the demagnetizing field of the second is
The reciprocity theorem states that
Magnetic charge and the pole-avoidance principle
Formally, the solution of the equations for the potential iswhere is the variable to be integrated over the volume of the body in the first integral and the surface in the second, and is the gradient with respect to this variable.
Qualitatively, the negative of the divergence of the magnetization (called a volume pole) is analogous to a bulk bound electric charge in the body while (called a surface pole) is analogous to a bound surface electric charge. Although the magnetic charges do not exist, it can be useful to think of them in this way. In particular, the arrangement of magnetization that reduces the magnetic energy can often be understood in terms of the pole-avoidance principle, which states that the magnetization tries to reduce the poles as much as possible.
Single domain
default direct SVG link
One way to remove the magnetic poles inside a ferromagnet is to make the magnetization uniform. This occurs in single-domain ferromagnets. This still leaves the surface poles, so division into domains
Magnetic domains
A magnetic domain describes a region within a magnetic material which has uniform magnetization. This means that the individual magnetic moments of the atoms are aligned with one another and they point in the same direction...
reduces the poles further. However, very small ferromagnets are kept uniformly magnetized by the exchange interaction
Exchange interaction
In physics, the exchange interaction is a quantum mechanical effect without classical analog which increases or decreases the expectation value of the energy or distance between two or more identical particles when their wave functions overlap...
.
The concentration of poles depends on the direction of magnetization (see the figure). If the magnetization is along the longest axis, the poles are spread across a smaller surface, so the energy is lower. This is a form of magnetic anisotropy
Magnetic anisotropy
Magnetic anisotropy is the direction dependence of a material's magnetic properties. In the absence of an applied magnetic field, a magnetically isotropic material has no preferential direction for its magnetic moment while a magnetically anisotropic material will align its moment with one of the...
called shape anisotropy.
Multiple domains
If the ferromagnet is large enough, its magnetization can divide into domainsMagnetic domains
A magnetic domain describes a region within a magnetic material which has uniform magnetization. This means that the individual magnetic moments of the atoms are aligned with one another and they point in the same direction...
. It is then possible to have the magnetization parallel to the surface. Within each domain the magnetization is uniform, so there are no volume poles, but there are surface poles at the interfaces (domain walls) between domains. However, these poles vanish if the magnetic moments on each side of the domain wall meet the wall at the same angle (so that the components are the same but opposite in sign). Domains configured this way are called closure domains.
Demagnetizing factor
An arbitrary shaped magnetic object has a total magnetic field that varies with location inside the object and can be quite difficult to calculate. This makes it very difficult to determine the magnetic properties of a material such as, for instance, how the magnetization of a material varies with the magnetic field. For a uniformly magnetized sphere in a uniform magnetic field the internal magnetic field is uniform:where is the magnetization of the sphere and is called the demagnetizing factor and equals for a sphere.
This equation can be generalized to include ellipsoids having principal axes in x,y, and z directions such that each component has a relationship of the form:
Other important examples are an infinite plate (an ellipsoid with two of its axes going to infinity) which has = in a direction normal to the plate and zero otherwise and an infinite cylinder (an ellipsoid with one of its axes tending toward infinity with the other two being the same) which has = along its axis. For tables or equations for the magnetizing factors of the general ellipsoid see .

