Degree of a continuous mapping
Encyclopedia
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the degree is a numerical invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
that describes a continuous mapping between two compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
oriented
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s of the same dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
. Intuitively, the degree represents the number of times that the domain manifold wraps around the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
manifold under the mapping. The degree is always an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, but may be positive or negative depending on the orientations.
The degree of a map was first defined by Brouwer
Luitzen Egbertus Jan Brouwer
Luitzen Egbertus Jan Brouwer FRS , usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, a graduate of the University of Amsterdam, who worked in topology, set theory, measure theory and complex analysis.-Biography:Early in his career,...
, who showed that the degree is a homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
invariant, and used it to prove the Brouwer fixed point theorem
Brouwer fixed point theorem
Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
. In modern mathematics, the degree of a map plays an important role in topology and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
. In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the degree of a continuous map (for instance a map from space to some order parameter set) is one example of a topological quantum number
Topological quantum number
In physics, a topological quantum number is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological considerations...
.
From Sn to Sn
The simplest and most important case is the degree of a continuous map from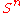 to itself (in the case
to itself (in the case  , this is called the winding number
, this is called the winding numberWinding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
):
Let :
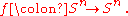 be a continuous surjective map. Then
be a continuous surjective map. Then  induces homomorphism
induces homomorphism 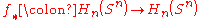 . Considering the fact that
. Considering the fact that 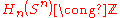 , we see that
, we see that  must be of the form
must be of the form  for some fixed
for some fixed 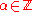 .
.This
 is then called the degree of
is then called the degree of  .
.Algebraic topology
Let X and Y be closed connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
oriented
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
m-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. Orientability of a manifold implies that its top homology group is isomorphic to Z. Choosing an orientation means choosing a generator of the top homology group.
A continuous map f : X→Y induces a homomorphism f* from Hm(X) to Hm(Y). Let [X], resp. [Y] be the chosen generator of Hm(X), resp. Hm(Y) (or the fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
of X, Y). Then the degree of f is defined to be f*([X]). In other words,
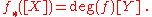
If y in Y and f -1(y) is a finite set, the degree of f can be computed by considering the m-th local homology groups
Relative homology
In algebraic topology, a branch of mathematics, the homology of a topological space relative to a subspace is a construction in singular homology, for pairs of spaces. The relative homology is useful and important in several ways...
of X at each point in f -1(y).
Differential topology
In the language of differential topology, the degree of a smooth map can be defined as follows: If f is a smooth map whose domain is a compact manifold and p is a regular value of f, consider the finite set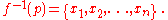
By p being a regular value, in a neighborhood of each xi the map f is a local diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
(it is a covering map
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
). Diffeomorphisms can be either orientation preserving or orientation reversing. Let r be the number of points xi at which f is orientation preserving and s be the number at which f is orientation reversing. When the domain of f is connected, the number r − s is independent of the choice of p and one defines the degree of f to be r − s. This definition coincides with the algebraic topological definition above.
The same definition works for compact manifolds with boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
but then f should send the boundary of X to the boundary of Y.
One can also define degree modulo 2 (deg2(f)) the same way as before but taking the fundamental class in Z2 homology. In this case deg2(f) is element of Z2, the manifolds need not be orientable and if n is the number of preimages of p as before then deg2(f) is n modulo 2.
Integration of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s gives a pairing between (C∞-)singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
and de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
: <[c], [ω]> = ∫cω, where [c] is a homology class represented by a cycle c and ω a closed form representing a de Rham cohomology class. For a smooth map f : X→Y between orientable m-manifolds, one has
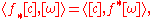
where f* and f* are induced maps on chains and forms respectively. Since f*[X] = deg f · [Y], we have
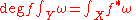
for any m-form ω on Y.
Maps from closed region
If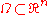 is a bounded region
is a bounded regionRegion (mathematical analysis)
In mathematical analysis, the word region usually refers to a subset of \R^n that is open , connected and non-empty. A closed region is sometimes defined to be the closure of a region....
,
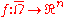 smooth,
smooth, 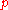 a regular value of
a regular value of  and
and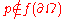 , then the degree
, then the degree 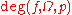 is defined
is definedby the formula
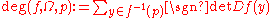
where
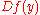 is the Jacobi matrix
is the Jacobi matrixJacobi matrix
Jacobi matrix may refer to:* Jacobian matrix and determinant of a smooth map between Euclidean spaces or smooth manifolds* Jacobi matrix, a tridiagonal symmetric matrix appearing in the theory of orthogonal polynomials...
of
 in
in 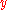 .
.This definition of the degree may be naturally extended for non-regular values
 such that
such that  where
where 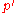 is a point close to
is a point close to 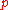 .
.The degree satisfies the following properties:
- If
 , then there exists
, then there exists  such that
such that 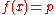 .
. -
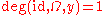 for all
for all 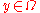 .
. - Decomposition property:
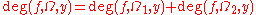 , if
, if 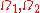 are disjoint parts of
are disjoint parts of  and
and 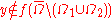 .
. - Homotopy invariance: If
 and
and 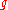 are homotopy equivalent via a homotopy
are homotopy equivalent via a homotopy  such that
such that 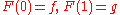 and
and  , then
, then 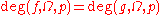
- The function
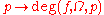 is locally constant on
is locally constant on 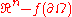
These properties characterise the degree uniquely and the degree may be defined by them in an axiomatic way.
In a similar way, we could define the degree of a map between compact oriented manifolds with boundary.
Properties
The degree of map is a homotopyHomotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
invariant; moreover for continuous maps from the sphere to itself it is a complete homotopy invariant, i.e. two maps
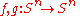 are homotopic if and only if
are homotopic if and only if  .
.In other words, degree is an isomorphism
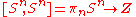 .
.Moreover, the Hopf theorem
Hopf theorem
The Hopf theorem is a statement in differential topology, saying that the topological degree is the only homotopy invariant of continuous maps to spheres.-Formal statement:...
states that for any
 -manifold
-manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M, two maps
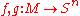 are homotopic if and only if
are homotopic if and only if 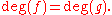
A map
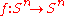 is extendable to a map
is extendable to a map 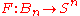 if and only if
if and only if  .
.See also
- Covering number, a similarly named term
- Polytope densityPolytope densityIn geometry, polytope density represents the number of windings of a polytope, particularly a uniform or regular polytope, around its center. It can be visually determined by counting the minimum number of facet crossings of a ray from the center to infinity...
, a polyhedral analog - Topological degree theoryTopological degree theoryIn mathematics, topological degree theory is a generalization of the winding number of a curve in the complex plane. It can be used to estimate the number of solutions of an equation, and is closely connected to fixed-point theory. When one solution of an equation is easily found, degree theory can...

